【时间序列预测】基于非线性时间序列预测的稀疏局部线性和邻域嵌入研究（Matlab代码实现）

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

目录

📋1 概述

📝2 运行结果

📃3 参考文献

📋4 Matlab代码、文章下载

---

📋1 概述

摘要
本文提出了一种基于字典的L1范数稀疏编码方法，用于时间序列预测。该方法无需训练阶段，且参数调整极少，适合非平稳和在线预测应用。预测过程被表述为一个L1范数的基追踪问题，针对每个测试向量估计一组稀疏权重。本文比较了包括稀疏局部线性嵌入和稀疏最近邻嵌入在内的约束稀疏编码公式。使用16个时间序列数据集测试了该方法在离线时间序列预测中的表现，其中训练数据是固定的。此外，还将所提出的方法与Bagging树（BT）、最小二乘支持向量回归（LSSVM）和正则化自回归模型进行了比较。结果表明，所提出的稀疏编码预测方法性能优于使用10折交叉验证的LSSVM，并显著优于正则化自回归和Bagging树。平均而言，在LSSVM完成训练的同时，可以完成数千次稀疏编码预测，这使得所提出的技术适合于在线预测和高度非平稳数据。
关键词：时间序列预测；稀疏编码；稀疏局部线性嵌入；邻域嵌入；非线性时间序列

---

I. 引言

时间序列预测一直是数十年来活跃的研究领域，涵盖了大量应用和算法。经典方法包括使用自回归和移动平均（ARMA）模型的线性预测以及非线性模型。机器学习方法，包括支持向量机、递归神经网络、模糊神经网络和集成神经网络及其组合，已被用于时间序列预测，并声称比经典技术表现更好。还有一些尝试用于非参数时间序列建模，例如使用矢量量化和基于K最近邻的回归。然而，这些技术使用经验方法来确定邻居数量、各自的权重和最优预测值。
最近，在不同的领域中，基于字典的L1范数稀疏编码在包括图像超分辨率、模式分类和信号建模的一类算法中取得了优异的结果。以图像超分辨率为例，训练阶段构建了两个字典：一个用于预测中使用的模式（低分辨率LR块），另一个用于对应的预测模式（高分辨率HR块）。给定一个测试LR块，使用第一个字典通过字典块的稀疏线性组合找到测试块的最小误差表示。相同的稀疏权重用于通过第二个字典构建HR块。时间序列预测可以在相同的框架内被看待：第一个字典包含预测训练向量，而第二个字典包含对应的目标值。给定一个测试模式，使用第一个字典中的向量通过稀疏权重的线性组合来构建该测试模式。本文的主要假设如下：由于每个构建向量都有其对应的目标值，因此我们想要预测的测试模式的目标值应该是构建向量目标值的加权组合，使用相同的稀疏构建权重。此外，由于测试模式通过最少数量的字典原子表示，从而实现了最小复杂性（例如通过贝叶斯推断实现良好的泛化和平滑预测）。这是由使用L1范数正则化的稀疏编码所赋予的优势，可以被视为具有拉普拉斯先验的贝叶斯预测。所提出的方法无需训练，使其非常适合在线预测。
本文的其余部分安排如下：第II节回顾相关工作，特别是[18]中给出的正则化自回归线性预测公式以及基于KNN的预测。第III节描述了所提出的稀疏编码预测算法及其变体的数学公式。第IV节详细介绍了16个数据集的实验结果和用于一步预测的数据集描述，第V节为结论。

V. 结论

本文提出了一种基于稀疏编码的时间序列一步预测方法。文中介绍了多种稀疏编码变体，这些变体采用了不同的约束L1正则化公式。通过控制稀疏解中允许的邻居数量，该方法在快速预测时间下实现了最佳性能，其平均归一化均方误差（NMSE）略优于最小二乘支持向量回归（LSSVM），显著优于Bagging树（BG）和自回归L1（AR-L1）。在16个一步非线性预测数据集上进行了测试。此外，与最近用于多步预测的加权K最近邻（KNN）方法相比，所提出的技术获得了更好的平均NMSE结果，并且由于无需训练阶段，因此适合于在线时间序列预测。

表II. NMSE、时间和稀疏性比较

技术	BG	LSSVM	SCU
NMSE	0.16	0.061	0.107
训练时间	32	84	0.0
测试时间	0.033	0.002	0.49
稀疏性	1270	1270	7
稀疏百分比	100%	100%	1.05%

技术	SLLE200	SNNE200	SKNN200
NMSE	0.062	0.057	0.057
训练时间	0.0	0.0	0.0
测试时间	0.36	0.45	0.017
稀疏性	19	14	28
稀疏百分比	2.6%	2.2%	3.1%

技术	SC1	SC2	SCW1
NMSE	0.059	0.056	0.055
训练时间	0.0	0.0	0.0
测试时间	0.44	1.07	0.42
稀疏性	29	93	18
稀疏百分比	3.93%	11.5%	2.4%

技术	SNNEG	LSL2	AR-L1
NMSE	0.067	0.261	0.198
训练时间	0.0	0.0	0.26
测试时间	0.59	0.34	0.01
稀疏性	5	742	1270
稀疏百分比	0.74%	67%	100%

表III. 最近邻数量的影响

技术	SNNE1	SNNE5	SNNE15
NMSE	0.144	0.095	0.085

技术	SKNN1	SKNN5	SKNN15
NMSE	NA	NA	0.089

技术	SLLE1	SLLE5	SLLE15
NMSE	NA	NA	0.093

技术	UKNN1	UKNN3	UKNN5
NMSE	0.1816	0.1828	0.1817

技术	L2KNN1	L2KNN3	L2KNN5
NMSE	0.1008	0.0657	0.0623

技术	SNNE25	SNNE50	SNNE200
NMSE	0.07	0.069	0.057

技术	SKNN25	SKNN50	SKNN200
NMSE	0.073	0.069	0.057

技术	SLLE25	SLLE50	SLLE200
NMSE	0.067	0.073	0.062

技术	UKNN7	UKNN9	UKNN20
NMSE	0.1821	0.1853	0.219

技术	L2KNN7	L2KNN9	L2KNN20
NMSE	0.0624	0.0642	0.0743

未来的研究将专注于使用贪婪算法来加快稀疏编码的求解速度。更重要的是，将稀疏编码方法应用于多步预测，其中目标字典包含向量而非标量值，以表示目标预测范围。

详细文章第4部分下载。

📝2 运行结果

 

 

 

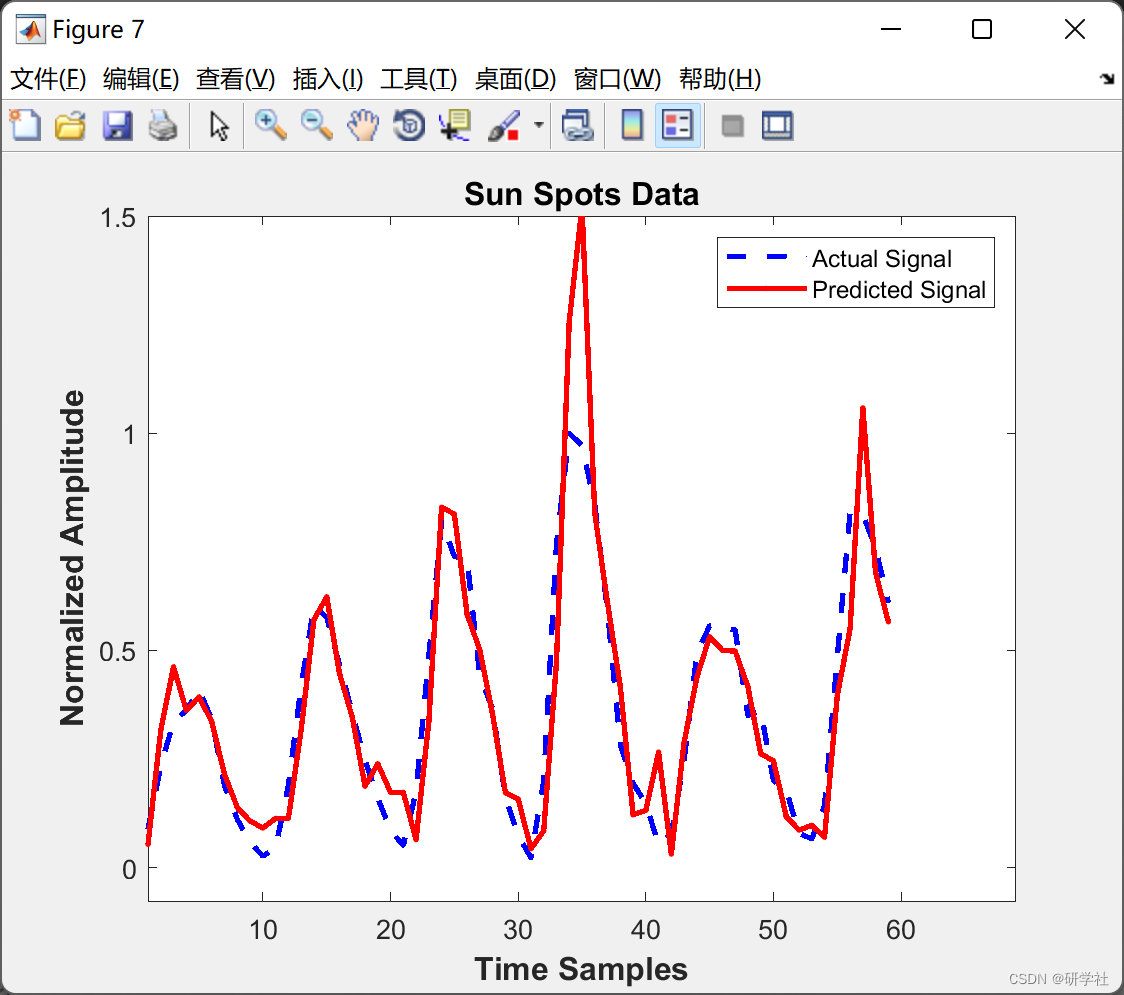
部分代码：

if(nnnn==1)    %Mackey-Glass data
load MGData;
a = MGData;
time = a(:, 1);
x_t = a(:, 2);
trn_data = zeros(500, 5);
chk_data = zeros(500, 5);
% prepare training data
trn_data(:, 1) = x_t(101:600);
trn_data(:, 2) = x_t(107:606);
trn_data(:, 3) = x_t(113:612);
trn_data(:, 4) = x_t(119:618);
trn_data(:, 5) = x_t(125:624);
% prepare checking data
chk_data(:, 1) = x_t(601:1100);
chk_data(:, 2) = x_t(607:1106);
chk_data(:, 3) = x_t(613:1112);
chk_data(:, 4) = x_t(619:1118);
chk_data(:, 5) = x_t(625:1124);
Train=trn_data;
Test=chk_data;
K=4;
delta=2;
eps=0.001;
C='Mackey Glass Data';

elseif(nnnn==2)
load Henon1      %Henon chaotic map data
x_t=Henon1;
sz=length(x_t);  
time = 1:sz;
Train = x_t(1:1004);   
Test  = x_t(1005:1259); 
%here we add the WGN with standard deviation of 0.05
nnn = 0.05*randn(1004,1);
Train = Train + nnn;    
K=4;
delta=2;
eps=0.001;
C = 'Henon Chaotic Map Data'

elseif(nnnn==3)     %Lorenz chaotic map data
load Lorenz1
x_t=Lorenz1;
sz=length(x_t);  
time = 1:sz;
Train = x_t(1:1004);   
Test  = x_t(1005:1259); 
nnn = 0.05*randn(1004,1);
Train = Train + nnn;
K=4;
delta=2;
eps=0.001;
C = 'Lorenz Chaotic Map Data';

elseif(nnnn==4)
load Rossler1     %Rossler
x_t=Rossler1;
sz=length(x_t);  
time = 1:sz;
Train = x_t(1:1004);   
Test  = x_t(1005:1259); 
%here we add the WGN with standard deviation of 0.05
nnn = 0.05*randn(1004,1);
Train = Train + nnn;
K=4;
delta=2;
eps=0.001;
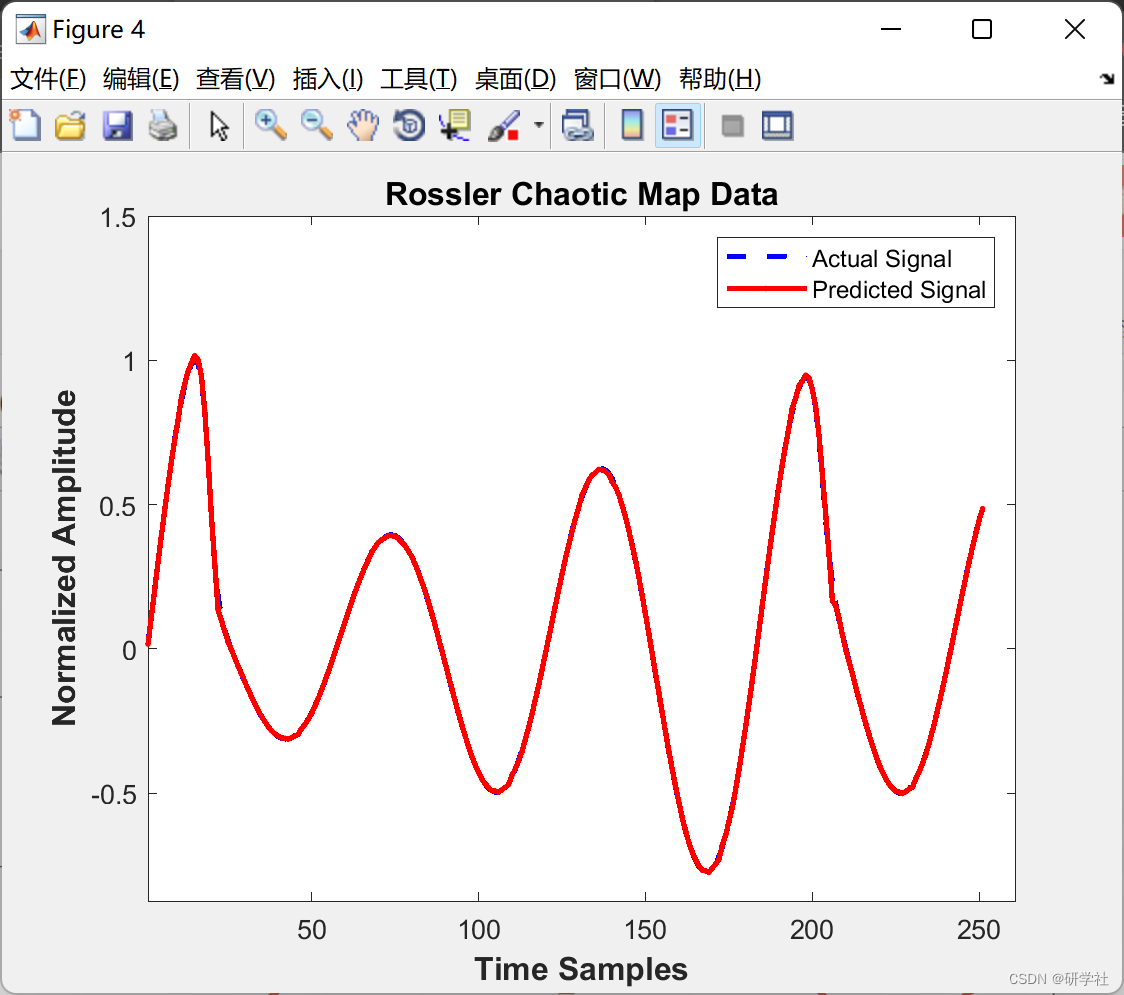
C = 'Rossler Chaotic Map Data';

elseif(nnnn==5)
load Nord1        %NordPool
x_t=Nord1;
sz=length(x_t);  
time = 1:sz;
Train = x_t(1:880);   
Test  = x_t(881:988);
K=9;   %as recommended by reference
delta=2;
eps=0.001;
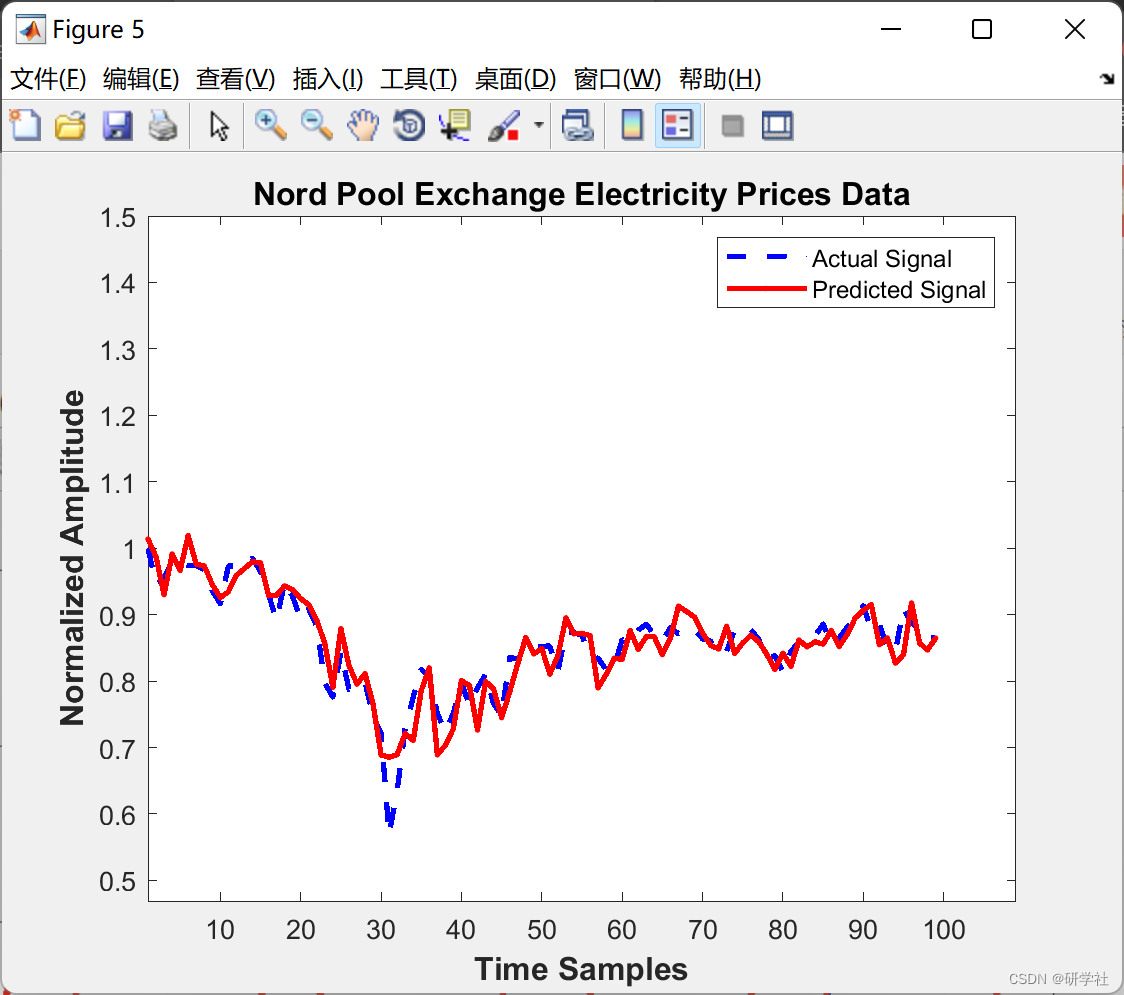
C= 'Nord Pool Exchange Electricity Prices Data';

📃3 参考文献

文章中一些内容引自网络，会注明出处或引用为参考文献，难免有未尽之处，如有不妥，请随时联系删除。(文章内容仅供参考，具体效果以运行结果为准)

📋4 Matlab代码、文章下载