14 隐马尔可夫模型HMM（Hidden Markov Model）

1 背景

机器学习大致可以分为两个派别，也就是频率派和贝叶斯派的方法，这个之前，我们都有过详细的说明。这里再大致的回顾一下。

• 频率派的思想就衍生出了统计学习方法，说白了统计学习方法的重点在于优化，找 loss function。 频率派的方法可以分成三步：

1. 定义 Model, 比如 $f(w)=w^{T}x+b$;
2. 寻找策略 strategy，也就是定义 Loss function;
3. 求解，也就是优化的方法，比如梯度下降 (GD)，随机梯度下降 (SGD)，牛顿法, 拟牛顿法等等。

• 贝叶斯派的思想也就衍生出了概率图模型。概率图模型重点研究的是一个 Inference 的问题，我们要求的是一个后验概率分布 $P(Z|X)$ , 其中 $X$ 为观测变量， $Z$ 为隐变量。实际上就是一个积分问题, 为什么呢？因为贝叶斯框架中的归一化因子需要对整个状态空间进行积分，非常的复杂。代表性的有前面讲到的 MCMC，MCMC 的提出才是彻底的把贝叶斯理论代入到实际的运用中。

1.1 概率图模型回顾

概率图模型，如果不考虑时序的关系，我们可以大致的分为：有向图的Bayesian Network 和无向图的Markov Random Field (Markov Network)。这样，我们根据分布获得的样本之间都是 $iid$ (独立同分布) 的。比如Gaussian Mixture Model (GMM)，我们从 $P(X|\theta )$ 的分布中采出 N 个样本 { x 1 , x 2 , ⋯   , x n } \left\{x_{1}, x_{2}, \cdots, x_{n}\right\} {x1​,x2​,⋯,xn​} N 个样本之间都是独立同分布的。也就是对于隐变量 $Z$, 观测变量 $X$ 之间，我们可以假设 $P(X|Z)=\mathcal{N}(\mu ,\Sigma )$ , 这样就可以引入我们的先验信息，从而简化 $X$ 的复杂分布。 如果引入了时间的信息，也就是 $x_i$ 之间不再是 $iid$ 的了，我们称之为 Dynamic Model。模型如下 所示：

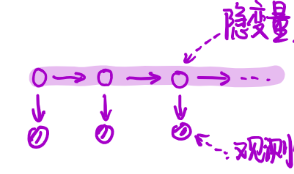
Dynamic Model 可以从两个层面来看，横着看就是 time 的角度，如果是竖着看就可以表达为 $P(X_j，Z)$ 的形式，也就是 Mixture 的形式。概率系统根据状态与状态之间的关系，可以分为两类。

• 如果是离散的则有HMM 算法。
• 如果是连续的，按照线性和非线性可以分为 Kalman Filter 和 Paricle Filter。

1.2 HMM 算法简介

Hidden Markov Model 的拓扑结构图如下所示：

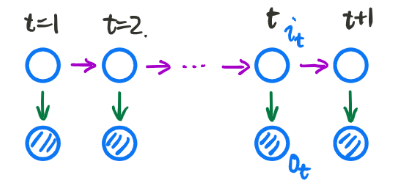
大家看到这个模型就会觉得和上一讲提到的，MCMC 模型方法有点类似。HMM 可以看做一个三元组 $\lambda =(\pi ,\mathcal{A},\mathcal{B})$ 。其中：
π : $\pi$: 是初始概率分布。
A : $\mathcal{A}$: 状态转移矩阵。
B : $\mathcal{B}$: 发射矩阵。

拓扑结构图的第二行为观测变量，观测变量 $O:o_1,o_2,\cdots ,o_t,\cdots \leftarrow \mathcal{V}=v_1,v_2,\cdots ,v_M$​ 。其中 $\mathcal{V}$ 是观察变量 $o$ 的值域，代表每一个观测变量 $o_i$​ 可能有 M 个状态。

拓扑结构图的第一行为状态变量，状态变量 $I:i_1,i_2,\cdots ,i_t,\cdots \leftarrow \mathcal{Q}=q_1,q_2,\cdots ,q_N$。其中 $\mathcal{Q}$ 是状态变量 $i$ 的值域，代表每一个状态变量 $i$ 可能有 N 个状态。

$\mathcal{A}=\left[a_{ij}\right]$ 表示状态转移矩阵, $a_{ij}=P\left(i_{i+1}=q_j|i_t=q_i\right)$
$\mathcal{B}=\left[b_j(k)\right]$ 表示发射矩阵, $b_j(k)=P\left(o_t=V_k|i_t=q_j\right)$

而 $\pi$ 是什么意思呢？假设当 $t$ 时刻的隐变量 $i_t$ ​, 可能有 { q 1 , q 2 , ⋯   , q N } \left\{q_{1}, q_{2}, \cdots, q_{N}\right\} {q1​,q2​,⋯,qN​} 个状态，而这些状态出现的概率分别为 { p 1 , p 2 , ⋯   , p N } \left\{p_{1}, p_{2}, \cdots, p_{N}\right\} {p1​,p2​,⋯,pN​} 。这就是一个关于 $i_t$​ 隐变量的离散随机分布。

$\mathcal{A}$ 表示为各个状态转移之间的概率。
$\mathcal{B}$ 表示为观测变量和隐变量之间的关系。

1.2.1 两个假设

这是有关 Hidden Markov Model 的两个假设：

1. 齐次 Markov 假设 (无后向性)：2. 观察独立假设。

1. 齐次马尔可夫假设：未来与过去无关，只依赖与当前的状态。也就是：
$$P\left(i_{t+1}|i_t,i_{t-1},\cdots ,i_1,o_t,\cdots ,o_1\right)=P\left(i_{t+1}|i_t\right)$$2. 观测独立假设：
$$P\left(o_t|i_t,i_{t-1},\cdots ,i_1,o_t,\cdots ,o_1\right)=P\left(o_t|i_t\right)$$

1.2.2 三个问题

1. Evaluation 的问题，我们要求的问题就是 $P(O|\lambda )$ 。也就是前向后向算法，给定一个模型 $\lambda$, 求出观测变量的概率分布。
2. Learning 的问题， $\lambda$ 如何求的问题。也就是 ${\lambda }_{MLE}=\arg {\max }_{\lambda }P(O|\lambda )$ 。求解的方法是 $\mathrm{E}\mathrm{M}$ 算 法和 Baum Welch 算法。
3. Decoding 的问题，状态序列为 $I$，也就是隐变量序列， $\hat{I}=\arg {\max }_{I}P(I|O,\lambda )$ 。也就是在观测变量 O 和 $\lambda$ 的情况下使隐变量序列 $I$ 出现的概率最大。而这个问题大致被分为预测和滤波。
   预测问题为： $P\left(i_{t+1}|o_1,\cdots ,o_t\right)$; 也就是在已知当前观测变量的情况下预测下一个状态，也就是 Viterbi 算法。
   滤波问题为： $P\left(i_t|o_1,\cdots ,o_t\right)$; 也就是求 $t$ 时刻的隐变量。即Kalman or Particle Filter

Hidden Markov Model，可以被我们总结成一个模型 $\lambda =(\pi ,\mathcal{A},\mathcal{B})$, 两个假设，三个问题。而其中我们关注得最多的就是 Decoding 的问题。

1.3 什么样的问题需要HMM模型

首先我们来看看什么样的问题解决可以用HMM模型。使用HMM模型时我们的问题一般有这两个特征：

1. 我们的问题是基于序列的，比如时间序列，或者状态序列。
2. 我们的问题中有两类数据，一类序列数据是可以观测到的，即观测序列；而另一类数据是不能观察到的，即隐藏状态序列，简称状态序列。

有了这两个特征，那么这个问题一般可以用HMM模型来尝试解决。这样的问题在实际生活中是很多的。比如：我现在在打字写博客，我在键盘上敲出来的一系列字符就是观测序列，而我实际想写的一段话就是隐藏序列，输入法的任务就是从敲入的一系列字符尽可能的猜测我要写的一段话，并把最可能的词语放在最前面让我选择，这就可以看做一个HMM模型了。再举一个，我在和你说话，我发出的一串连续的声音就是观测序列，而我实际要表达的一段话就是状态序列，你大脑的任务，就是从这一串连续的声音中判断出我最可能要表达的话的内容。

从这些例子中，我们可以发现，HMM模型可以无处不在。但是上面的描述还不精确，下面我们用精确的数学符号来表述我们的HMM模型。

2 Evaluation

Evaluation 的问题可以被我们描述为：给定一个 $\lambda$，如何求得 $P(O|\lambda )$。也就是在给定模型 $\lambda$ 的情况下，求某个观测序列出现的概率。

2.1 模型求解

对于 $P(O|\lambda )$ 我们利用概率的基础知识进行化简可以得到:
$$P(O|\lambda )=\sum _{I}P(O,I|\lambda )=\sum _{I}P(O|I,\lambda )P(I|\lambda )$$其中 ${\sum }_I$​ 表示所有可能出现的隐状态序列 ; ${\sum }_{I}P(O|I,\lambda )$ 表示在某个隐状态下，产生某个观测序列的概率; $P(I|\lambda )$ 表示某个隐状态出现的概率。
那么：
$$\begin{array}{rl}P(I|\lambda )& =P\left(i_1,\cdots ,i_T|\lambda \right)\\ & =P\left(i_T|i_1,\cdots ,i_{T-1},\lambda \right)\cdot P\left(i_1,\cdots ,i_{T-1}|\lambda \right)\end{array}$$
根据 Hidden Markov Model 两个假设中的,齐次马尔可夫假设,我们可以得到: $P\left(i_T|i_1,\cdots ,i_{T-1},\lambda \right)=P\left(i_T|i_{T-1}\right)=a_{i_{T-1},i_T}$​​。 后面按照一样的思路进行迭代就可以了。那么我们继续对上式进行化简可以得到：
$$\begin{array}{rl}P\left(i_T|i_1,\cdots ,i_{T-1},\lambda \right)\cdot P\left(i_1,\cdots ,i_{T-1}|\lambda \right)& =P\left(i_T|i_{T-1}\right)\cdot P\left(i_1,\cdots ,i_{T-1}|\lambda \right)\\ & =a_{i_{T-1},i_T}\cdot a_{i_{T-2},i_{T-1}}\cdots a_{i_1,i_2}\cdot \pi \left(a_{i_1}\right)\\ & =\pi \left(a_{i_1}\right)\prod _{t=2}^T{a}_{i_{i-1},i_t}\end{array}$$然后，运用观察独立假设，我们可以知道：
$$\begin{array}{rl}P(O|I,\lambda )& =P\left(o_1,o_2,\cdots ,o_T|I,\lambda \right)\\ & =\prod _{t=1}^{T}P\left(o_t|I,\lambda \right)\\ & =\prod _{t=1}^T{b}_{i_t}\left(o_t\right)\end{array}$$

那么，结合公式 (2-5)，我们可以得到：
$$\begin{array}{rl}P(O|\lambda )& =\sum _I\pi \left(a_{i_1}\right)\prod _{t=2}^T{a}_{i_{t-1},i_t}\prod _{t=1}^T{b}_{i_t}\left(o_t\right)\\ & =\sum _{i_1}\cdot \sum _{i_2}\cdots \sum _{i_T}\pi \left(a_{i_1}\right)\prod _{t=2}^T{a}_{i_{t-1},i_t}\prod _{t=1}^T{b}_{i_t}\left(o_t\right)\end{array}$$因为一共有 $T$ 个状态，每个状态有 $N$ 种可能，所以算法复杂度为 $O\left(N^T\right)$。 题然这样直接求太困难了，我们就需要另外想办法。

2.2 Forward Algorithm

⽤前向算法来解决复杂度⼤的问题。下面，我们首先展示一下Hidden Markov Model 的拓扑结构图:

我们记， ${\alpha }_t(i)=P\left(o_1,\cdots ,o_t,i_t=q_i|\lambda \right)$, 这个公式表示的是在之前所有的观测变量的前提下求出当前时刻的隐变量的概率。那么：
$$P(O|\lambda )=\sum _{i=1}^{N}P\left(O,i_t=q_i|\lambda \right)=\sum _{i=1}^N{\alpha }_t(i)$$其中， ${\sum }_{i=1}^N$​ 表示对所有可能出现的隐状态情形求和，而 ${\alpha }_t(i)$ 表示对所有可能出现的隐状态情形。我们的想法自然就是寻找 ${\alpha }_t(i)$ 和 ${\alpha }_t(i+1)$ 之间的关系，这样通过递推，我们就可以得到整个观测序列出现的概率。
那么，下面我们来进行推导：
$${\alpha }_t(i+1)=P\left(o_1,\cdots ,o_t,o_{t+1},i_{t+1}=q_j|\lambda \right)$$因为 ${\alpha }_t(i)$ 里面有 $i_t=q_j$, 我们就要想办法把 $i_t$​ 给塞进去，所以：
$$\begin{array}{rl}{\alpha }_t(i+1)& =P\left(o_1,\cdots ,o_t,o_{t+1},i_{t+1}=q_j|\lambda \right)\\ & =\sum _{i=1}^{N}P\left(o_1,\cdots ,o_t,o_{t+1},i_t=q_i,i_{t+1}=q_j|\lambda \right)\\ & =\sum _{i=1}^{N}P\left(o_{t+1}|o_1,\cdots ,o_t,i_t=q_i,i_{t+1}=q_j,\lambda \right)\cdot P\left(o_1,\cdots ,o_t,i_t=q_i,i_{t+1}=q_j|\lambda \right)\end{array}$$又根据观测独立性假设, 我们可以很显然的得到
$$P\left(o_{t+1}|o_1,\cdots ,o_t,i_t=q_i,i_{t+1}=q_j,\lambda \right)=P\left(o_{t+1}|i_{t+1}=q_j\right)$$ 所以：
$$\begin{array}{rl}{\alpha }_t(i+1)& =\sum _{i=1}^{N}P\left(o_{t+1}|o_1,\cdots ,o_t,i_t=q_i,i_{t+1}=q_j,\lambda \right)\cdot P\left(o_1,\cdots ,o_t,i_t=q_i,i_{t+1}=q_j|\lambda \right)\\ & =\sum _{i=1}^{N}P\left(o_{t+1}|i_{t+1}=q_j\right)\cdot P\left(o_1,\cdots ,o_t,i_t=q_i,i_{t+1}=q_j|\lambda \right)\end{array}$$
看到这个化简后的公式，我们关注一下和 ${\alpha }_t(i)$ 相比，好像还多了一项 $i_{t+1}=q_j$​, 我们下一步的工作就是消去它。所以：
$$P\left(o_1,\cdots ,o_t,i_t=q_i,i_{t+1}=q_j|\lambda \right)=P\left(i_{t+1}=q_j|o_1,\cdots ,o_t,i_t=q_i,\lambda \right)\cdot P\left(o_1,\cdots ,o_t,i_t=q_i|\lambda \right)$$
根据齐次马尔可夫性质，我们可以得到 $P\left(i_{t+1}=q_j|o_1,\cdots ,o_t,i_t=q_i,\lambda \right)=P\left(i_{t+1}=q_j|i_t=q_i\right)$
所以根据以上的推导，我们可以得到：
$$\begin{array}{rl}{\alpha }_{t+1}(j)& =\sum _{i=1}^{N}P\left(o_{t+1}|i_{t+1}=q_j\right)\cdot P\left(i_{t+1}=q_j|i_t=q_i\right)\cdot P\left(o_1,\cdots ,o_t,i_t=q_i|\lambda \right)\\ & =\sum _{i=1}^N{b}_j\left(o_{t+1}\right)\cdot a_{ij}\cdot {\alpha }_t(i)\end{array}$$经过上述的推导，我们就成功的得到了 ${\alpha }_{t+1}(j)$ 和 ${\alpha }_t(i)$ 之间的关系。通过这个递推关系，就可以遍历整个 Markov Model 了。这个公式是什么意思呢？它可以被我们表达为，所有可能出现的隐变量状态乘以转移到状态 $j$ 的概率，乘以根据隐变量 $i_{t+1}$​ 观察到 $o_{t+1}$​ 的概率，乘上根据上一个隐状态观察到的观察变量的序列的概率。 我们可以用一个图来进行表示：

其实读神经网络了解的同学就会发现，这实际上和前向传播神经网络非常的像，实际上就是状态的值乘以权重。也就是对于上一个隐状态的不同取值分别计算概率之后再求和。这样每次计算，有隐状态的状态空间数为N，序列的长度为T，那么总的时间复杂度为 $O(T{N}^2)$ 。

时间复杂度是怎么算出来的？

算法小结

2.3 Backward Algorithm

后向概率的推导实际上比前向概率的理解要难一些，前向算法实际上是一个联合概率，而后向算法则是一个条件概率，所以后向的概率实际上比前向难求很多。

我们设 ${\beta }_t(i)=P\left(o_{t+1},\cdots ,o_T|i_t=q_i,\lambda \right)$, 以此类推 , ${\beta }_t(1)=P\left(o_2,\cdots ,o_T|i_1=q_i,\lambda \right)$ 。我们的目标是计算 $P(O|\lambda )$ 的概率，我们首先来推导一下这个公式：
$$\begin{array}{rl}P(O|\lambda )& =P\left(o_1,o_2,\cdots ,o_N|\lambda \right)\\ & =\sum _{i=1}^{N}P\left(o_1,o_2,\cdots ,o_N,i_1=q_i|\lambda \right)\\ & =\sum _{i=1}^{N}P\left(o_1,o_2,\cdots ,o_N|i_1=q_i,\lambda \right)P\left(i_1=q_i|\lambda \right)\\ & =\sum _{i=1}^{N}P\left(o_1|o_2,\cdots ,o_N,i_1=q_i,\lambda \right)\cdot P\left(o_2,\cdots {,}_N,i_1=q_i|\lambda \right)\cdot {\pi }_i\\ & =\sum _{i=1}^{N}P\left(o_1|i_1=q_i,\lambda \right)\cdot {\beta }_1(i)\cdot {\pi }_i\\ & =\sum _{i=1}^N{b}_i\left(o_1\right)\cdot {\pi }_i\cdot {\beta }_1(i)\end{array}$$
现在我们已经成功的找到了 $P(O|\lambda )$ 和第一个状态之间的关系。其中， ${\pi }_i$ 为某个状态的初始状态的概率， $b_i\left(o_1\right)$表示为第 $i$ 个隐变量产生第 1 个观测变量的概率， ${\beta }_1(i)$ 表示为第一个观测状态确定以后生成后面观测状态序列的概率。结构图如下所示：

那么，我们下一步要通过递推，找到最后一个状态与第一个状态之间的关系。下面做如下的推导：
$$\begin{array}{rl}{\beta }_t(i)& =P\left(o_{t+1},\cdots ,o_T|i_t=q_i\right)\\ & =\sum _{j=1}^{N}P\left(o_{t+1},\cdots ,o_T,i_{t+1}=q_j|i_t=q_i\right)\\ & =\sum _{j=1}^{N}P\left(o_{t+1},\cdots ,o_T|i_{t+1}=q_j,i_t=q_i\right)\cdot \underset{a_{ij}}{\underbrace{P\left(i_{t+1}=q_j|i_t=q_i\right)}}\\ & =\sum _{j=1}^{N}P\left(o_{t+1},\cdots ,o_T|i_{t+1}=q_j\right)\cdot a_{ij}\\ & =\sum _{j=1}^{N}P\left(o_{t+1}|o_{t+2}\cdots ,o_T,i_{t+1}=q_j\right)\cdot \underset{{\beta }_{t+1}(j)}{\underbrace{P\left(o_{t+2}\cdots ,o_T|i_{t+1}\right)}}\cdot a_{ij}\\ & =\sum _{j=1}^{N}P\left(o_{t+1}|i_{t+1}=q_j\right)\cdot {\beta }_{t+1}(j)\cdot a_{ij}\\ & =\sum _{j=1}^N{b}_j\left(o_{t+1}\right)\cdot {\beta }_{t+1}(j)\cdot a_{ij}\end{array}$$
其中第三行到第四行的推导 $P\left(o_{t+1},\cdots ,o_T|i_{t+1}=q_j,i_t=q_i\right)=P\left(o_{t+1},\cdots ,o_T|i_{t+1}=q_j\right)$ 使用的马尔可夫链的性质，每一个状态都是后面状态的充分统计量，与之前的状态无关。通过这样的迭代从后往前推，我们就可以得到 β${\beta }_i(1)$ 的概率，从而推断出 $P(O|\lambda )$ 。整体的推断流程图如下图所示：

所以，可以通过求 ${\beta }_t(i)$ 进而求得 $P(O|\lambda )$

后推导没看懂？

3 Learning

首先我们回顾一下，上一节讲的有关 Evaluation 的问题。Evaluation 可以被我们描述为在已知模型 $\lambda$ 的情况下，求观察序列的概率。也就是：
$$P(O|\lambda )=\sum _{I}P(O,I|\lambda )=\sum _{i_1}\cdots \sum _{i_T}{\pi }_{i_i}\prod _{t=2}^T{a}_{i_{i-1},i_i}\prod _{t=1}^T{b}_{i_1}\left(o_t\right)$$此时的算法复杂度为 $O(N^T)$ 。算法的复杂度太高了，所以，就有了后来的 forward 和 backward 算法。那么就有如下定义：
$$\begin{array}{l}{\alpha }_t(i)=P\left(o_1,\cdots ,o_t,i_t=q_i|\lambda \right)\\ \\ {\beta }_t(i)=P\left(o_{t+1},\cdots ,o_T|i_t=q_i,\lambda \right)\\ \\ {\alpha }_T(i)=P\left(O,i_T=q_i\right)\to P(O|\lambda )={\sum }_{i=1}^N{\alpha }_T(i)\\ \\ {\beta }_1(i)=P\left(o_2,\cdots ,o_T|i_1=q_i,\lambda \right)\to P(O|\lambda )={\sum }_{i=1}^N{\pi }_i{b}_i\left(o_1\right){\beta }_1(i)\end{array}$$
而使用 forward 和 backward 算法的复杂度为 $O(T{N}^2)$ 。这一节，我们就要分析 Learning 的部分， Learning 就是要在已知观测数据的情况下求参数 $\lambda$, 也就是：
$${\lambda }_{MLE}=\arg \underset{\lambda }{\max }P(O\mid \lambda )$$

3.1 Learning:已知 $O$，求 $\lambda$

问题描述：我们有D个观测序列 $i_1,i_2,\cdots ,i_D$​，每个序列长度是T，需要求出初始分布 $\pi$，状态转移矩阵A，和发射矩阵B。
Baum-Welch算法是使用EM方法解决这个问题的算法。

我们需要计算的目标是：
$${\lambda }_{MLE}=\arg \underset{\lambda }{\max }P(O|\lambda )$$又因为: $$P(O|\lambda )=\sum _{i_1}\cdots \sum _{i_T}{\pi }_{i_1}\prod _{t=2}^T{a}_{i_{t-1},i_t}\prod _{t=1}^T{b}_{i_1}\left(o_t\right)$$对这个方程的 $\lambda$ 求偏导，实在是太难算了。所以，我们考虑使用 EM 算法。我们先来同顾一下 EM 算法：
$${\theta }^{(t+1)}=\arg \underset{\theta }{\max }{\int }_z\log P(X,Z|\theta )\cdot P\left(Z|X,{\theta }^{(t)}\right)dZ$$而 $X\to O$ 为观测变量 ; $Z\to I$ 为隐变量，其中 $I$ 为离散变量; $\theta \to \lambda$ 为参数。那么，我们可以将公式改写为：
$${\lambda }^{(t+1)}=\arg \underset{\lambda }{\max }\sum _I\log P(O,I|\lambda )\cdot P\left(I|O,{\lambda }^{(t)}\right)$$这里的 ${\lambda }^{(t)}$ 是一个常数，而
$$P\left(I|O,{\lambda }^{(t)}\right)=\frac{P\left(I,O|{\lambda }^{(t)}\right)}{P\left(O|{\lambda }^{(t)}\right)}$$并且 $P\left(O|{\lambda }^{(t)}\right)$ 中 ${\lambda }^{(t)}$ 是常数，所以这项是个定量，与 $\lambda$ 无关, 所以 $\frac{P\left(I,O|{\lambda }^{(t)}\right)}{P(O|\lambda (t))}\propto P\left(I,O|{\lambda }^{(t)}\right)$ 。所以，我们可以将 ${\lambda }^{(t+1)}$ 改写为：
$${\lambda }^{(t+1)}=\arg \underset{\lambda }{\max }\sum _I\log P(O,I|\lambda )\cdot P\left(I,O|{\lambda }^{(t)}\right)$$这样做有什么目的呢？很显然这样可以把 $\log P(O,I|\lambda )$ 和 $P\left(I,O|{\lambda }^{(t)}\right)$ 变成一种形式。其中, ${\lambda }^{(t)}=\left({\pi }^{(t)},{\mathcal{A}}^{(t)},{\mathcal{B}}^{(t)}\right)$ , 而 ${\lambda }^{(t+1)}=\left({\pi }^{(t+1)},{\mathcal{A}}^{(t+1)},{\mathcal{B}}^{(t+1)}\right)$
我们定义：
$$Q\left(\lambda ,{\lambda }^{(t)}\right)=\sum _I\log P(O,I|\lambda )\cdot P\left(O,I|{\lambda }^{(t)}\right)$$而其中,
$$P(O|\lambda )=\sum _{i_1}\cdots \sum _{i_T}{\pi }_{i_1}\prod _{t=2}^T{a}_{i_{i-1},i_t}\prod _{t=1}^T{b}_{i_1}\left(o_t\right)$$所以,
$$Q\left(\lambda ,{\lambda }^{(t)}\right)=\sum _I\left[\left(\log {\pi }_{i_1}+\sum _{t=2}^T\log a_{i_{i-1},i_t}+\sum _{t=1}^T\log b_{i_t}\left(o_t\right)\right)\cdot P\left(O,I|{\lambda }^{(t)}\right)\right]$$

3.2 求 ${\pi }^{(t+1)}$

这小节中我们以 ${\pi }^{(t+1)}$ 为例，在公式 $Q\left(\lambda ,{\lambda }^{(t)}\right)$ 中 , ${\sum }_{t=2}^T\log a_{i_{l-1},i_c}$​​ 与 ${\sum }_{t=1}^T\log b_{i_i}\left(o_t\right)$ 与 $\pi$ 无关,
所以,
$$\begin{array}{rl}{\pi }^{(t+1)}& =\arg \underset{\pi }{\max }Q\left(\lambda ,{\lambda }^{(t)}\right)\\ & =\arg \underset{\pi }{\max }\sum _I\left[\log {\pi }_{i_1}\cdot P\left(O,I|{\lambda }^{(t)}\right)\right]\\ & =\arg \underset{\pi }{\max }\sum _{i_1}\cdots \sum _{i_T}\left[\log {\pi }_{i_1}\cdot P\left(O,i_1,\cdots ,i_T|{\lambda }^{(t)}\right)\right]\end{array}$$我们观察 { i 2 , ⋯   , i T } \left\{i_{2}, \cdots, i_{T}\right\} {i2​,⋯,iT​} 就可以知道，联合概率分布求和可以得到边缘概率。所以：
$$\begin{array}{rl}{\pi }^{(t+1)}& =\arg \underset{\pi }{\max }\sum _{i_1}\left[\log {\pi }_{i_1}\cdot P\left(O,i_1|{\lambda }^{(t)}\right)\right]\\ & =\arg \underset{\pi }{\max }\sum _{i=1}^N\left[\log {\pi }_i\cdot P\left(O,i_1=q_i|{\lambda }^{(t)}\right)\right]\left(\text{s.t.}\sum _{i=1}^N{\pi }_i=1\right)\end{array}$$

3.2.1 拉格朗日乘子法求解

根据拉格朗日乘子法，我们可以将损失函数写成：
$$\mathcal{L}(\pi ,\eta )=\sum _{i=1}^N\log {\pi }_i\cdot P\left(O,i_1=q_i|{\lambda }^{(t)}\right)+\eta \left(\sum _{i=1}^N{\pi }_i-1\right)$$使似然函数最大化，则是对损失函数 $\mathcal{L}(\pi ,\eta )$ 求偏导，则为：
$$\begin{array}{l}\frac{\mathcal{L}}{{\pi }_i}=\frac{1}{{\pi }_i}P\left(O,i_1=q_i|{\lambda }^{(t)}\right)+\eta =0\\ \\ P\left(O,i_1=q_i|{\lambda }^{(t)}\right)+{\pi }_i\eta =0\end{array}$$又因为 ${\sum }_{i=1}^N{\pi }_i=1$, 所以，我们将公式 (17) 进行求和，可以得到：
$$\sum _{i=1}^N\left(P\left(O,i_1=q_i|{\lambda }^{(t)}\right)+{\pi }_i\eta \right)=0\Rightarrow P\left(O|{\lambda }^{(t)}\right)+\eta =0$$所以，我们解得 $\eta =-P\left(O|{\lambda }^{(t)}\right)$, 由 $P\left(O,i_1=q_i|{\lambda }^{(t)}\right)+{\pi }_i\eta =0$ 从而推出：
$${\pi }_i^{(t+1)}=\frac{P\left(O,i_1=q_i|{\lambda }^{(t)}\right)}{P\left(O|{\lambda }^{(t)}\right)}$$进而，我们就可以推导出 ${\pi }^{(t+1)}=({\pi }_1^{(t+1)},{\pi }_2^{(t+1)},\cdots ,{\pi }_N^{(t+1)})$ 而 ${\mathcal{A}}^{(t+1)}$ 和 ${\mathcal{B}}^{(t+1)}$ 也都是同样的求法。这就是大名鼎鼎的 Baum Welch 算法，实际上思路和 EM 算法一致。不过在 Baum Welch 算法诞生之前，还没有系统的出现 EM 算法的归纳。所以，这个作者还是很厉害的。

3.3 求 $A^{(t+1)}$

3.4 求 $B^{(t+1)}$

4 Decoding：已知 $O,\lambda$,求 $I$

Vertibi算法的思想：Vertibi是一种动态规划算法，将序列 $i_1,i_2,\cdots ,i_T$ ​看作是路径的选择，总共有 $N^T$ 条路径，我们需要找出概率最大的路径。

具体的说，Decoding 问题可被我们描述为：
$$\hat{I}=\arg \underset{I}{\max }P(I|O,\lambda )$$也就是在给定观察序列的情况下，寻找最大概率可能出现的隐概率状态序列。也有人说 Decoding 问题是预测问题,但是实际上这样说是并不合适的。预测问题应该是 , $P\left(o_{t+1}|o_1,\cdots ,o_t\right)$ 和 $P\left(i_{t+1}|o_1,\cdots ,o_t\right)$ 这里的 $P\left(i_1,\cdots ,i_t|o_1,\cdots ,o_t\right)$ 看成是预测问题显然是不合适的。

4.1 Decoding Problem

下面我们展示一下Hidden Markov Model 的拓扑模型：

这里实际上就是一个动态规划问题，这里的动态规划问题实际上就是最大概率问题，只不过将平时提到的最大距离问题等价于最大概率问题，理论上都是一样的。每个时刻都有 N 个状态，所有也就是从 $N^T$ 个可能的序列中找出概率最大的一个序列，实际上就是一个动态规划问题，如下图所示：

我们假设：
$${\delta }_t(i)=\underset{i_1,\cdots ,i_{t-1}}{\max }P\left(o_1,\cdots ,o_t,i_1,\cdots ,i_{t-1},i_t=q_i\right)$$

这个等式是什么意思呢？ 也就是当 $t$ 个时刻是 $q_i$​, 前面 $t-1$ 个随便走，只要可以到达 $q_i$ 这个状态就行，而从中选取概率最大的序列。我们下一步的目标就是在知道 ${\delta }_t(i)$ 的情况下如何求 ${\delta }_t(i+1)$ 那么这样就能通过递推来求得知道最后一个状态下概率最大的序列。 ${\delta }_t(i+1)$ 的求解方法如下所示：

所以，
$$\begin{array}{rl}{\delta }_{t+1}(j)& =\underset{i_1,\cdots ,i_t}{\max }P\left(o_1,\cdots ,o_{t+1},i_1,\cdots ,i_t,i_{t+1}=q_j\right)\\ & =\underset{i_1,\cdots ,i_t}{\max }{\delta }_t(i)\cdot a_{ij}\cdot b_j\left(o_{t+1}\right)\end{array}$$这就是 Viterbi 算法，但是这个算法最后求得的是一个值，没有办法求得路径，如果要想求得路径，我们需要引入一个变量：
$${\phi }_{t+1}(j)=\arg \underset{1\le i\le N}{\max }{\delta }_t(i)\cdot a_{ij}\cdot b_j\left(o_{t+1}\right)$$这个函数用来干嘛的呢？他是来记录每一次迭代过程中经过的状态的 index。这样我们最终得到的 { φ 1 , φ 2 , ⋯   , φ T } \left\{\varphi_{1}, \varphi_{2}, \cdots, \varphi_{T}\right\} {φ1​,φ2​,⋯,φT​}, 就可以得到整个路径了。

5 小结

Hidden Markov Model 实际上是一个 Dynamic Model。我们以 Guassian Mixture Model (GMM)为例。对于一个观测状态，在隐变量状态给定的情况下，是符合一个 Gaussian Distribution，也就是 $D\left(O|i_1\right)\sim \mathcal{N}(\mu ,\Sigma )$ 。如果加入了 $\mathrm{time}$ 的因素就是 Hidden Markov Model，而其中 { i 1 , i 2 , ⋯   , i T } \left\{i_{1}, i_{2}, \cdots, i_{T}\right\} {i1​,i2​,⋯,iT​} 是离散的就行，这些我们在第一章的背景部分有过讨论。而观测变量 $o_1$​ 是离散的还是连续的都不重要。

5.1 Hidden Markov| Model 简介

Hidden Markov Model，可以用一个模型，两个假设和是三个问题来描述。

• 一个模型就是指 $\lambda =(\pi ,\mathcal{A},\mathcal{B})$ 。其中， $\pi$: 指的是初始概率分布 ; $\mathcal{A}$: 指的是状态转移矩阵 ; $\mathcal{B}$: 指的是发射矩阵，也就是在已知隐变量的情况下，得到观测变量的概率分布。
• 两个假设：

1. 齐次马尔可夫模型，马尔科夫性质中非常重要的一条。
2. 观测独立假设，也就是观测变量只和当前的隐变量状态有关。

• 三个问题：

1. Evaluation： $P(O|\lambda )$, 也就是在在已知模型的情况下，求观测变量出现的概率。
2. 2 Learning: $\hat{\lambda }=\arg {\max }_{\lambda }P(O|\lambda )$, 在已知观测变量的情况下求解隐马尔可夫模型的参数。
3. Decoding: $P(I|O)=P\left(i_1,\cdots ,i_t|o_1,\cdots ,o_t\right)$, 用公式的语言描述就是 $\hat{I}=\arg {\max }_{I}P(I,O|\lambda )$

5.2 Dynamic Model

Dynamic Model 实际上就是一个State Space Model，通常我们可以将Dynamic Model 的问题分成两类。

• 第一类为Learning 问题，即为，参数 $\lambda$ 是未知的，通过数据来知道参数是什么；
• 第二类就是Inference 问题，也就是在 $\lambda$ 未知的情况下，推断后验概率。实际上，我们需要求的就是 $P(Z|X)$，其中 X = { x 1 , x 2 , ⋯   , x T } X = \left\{x_{1}, x_{2}, \cdots, x_{T}\right\} X={x1​,x2​,⋯,xT​} 数据之间不是i.i.d 的。
  Inference 问题大概可以被分成：
  

5.3 整体框架

5.3.1 Learning

Learing 问题中 $\lambda$ 是已知的， ${\lambda }_{MLE}=argma{x}_{\lambda }P(X|\lambda )$。我们采用的是Baum Welch Algorithm，算法思想上和EM 算法类似，实际上也是Forward-Backward 算法。

5.3.2 Inference

5.3.2.1 Decoding

这里前面已经做出过详细的描述了，这里就不再展开进行描述了，主要可以概括为：在已知观测数据序列的情况下,求得出现概率最大的隐变量序列, 被我们描述为: $Z=\arg {\max }_{z}P\left(z_1,\cdots ,z_t|x_1,\cdots ,x_t\right)$
我们使用的一种动态规划的算法，被称为 Viterbi Algorithm|。

5.3.2.2 Prob of Evidence

在还有大家应该见得比较多的 Prob of Evidence 问题，也就是： $P(X|\theta )=P\left(x_1,\cdots ,x_t|\theta \right)$ 。我们通俗的称之为证据分布，实际上就是我们前面讲到的 Evaluation 方法。也就是在已知参数的情况下， 求观测数据序列出现的概率，用公式描述即为： $P(X|\theta )=P\left(x_1,x_2,\cdots ,x_t|\theta \right)$

5.3.2.3 Filtering

实际上是一个 Online-Learning 的过程，也就是如果不停的往模型里面喂数据，我们可以得到概率分布为： $P\left(z_t|x_1,\cdots ,x_t\right)$ 。所以 Filtering 非常的适合与 online update。我们要求的这个就是隐变量的边缘后验分布。为什么叫滤波呢？这是由于我们求的后验是 $P\left(z_t|x_1,\cdots ,x_t\right)$, 运用到了大量的历史信息，比 $P\left(z_t|x_t\right)$ 的推断更加的精确，可以过滤掉更多的噪声，所以被我们称为“过滤”。求解过程如下所示：
$$P\left(z_t|x_{1:t}\right)=\frac{P\left(z_t,x_1,\cdots ,x_t\right)}{P\left(x_1,\cdots ,x_t\right)}=\frac{P\left(z_t,x_1:x_t\right)}{{\sum }_{z_t}P\left(z_t,x_1:x_t\right)}\propto P\left(z_t,x_1:x_t\right)$$

5.3.3.4 Smoothing

Smoothing 问题和 Filtering 问题的性质非常的像，不同的是，Smoothing 问题需要观测的是一个不变的完整序列。对于 Smoothing 问题的计算，前面的过程和 Filtering 一样，都是：
$$P\left(z_t|x_{1:T}\right)=\frac{P\left(z_t,x_1,\cdots ,x_T\right)}{P\left(x_1,\cdots ,x_T\right)}=\frac{P\left(z_t,x_1:x_T\right)}{{\sum }_{z_t}P\left(z_t,x_1:x_T\right)}\propto P\left(z_t,x_1:x_T\right)$$同样因为 ${\sum }_{z_t}P\left(z_t,x_1:x_T\right)$ 是一个归一化常数, 我们这里不予考虑。下面的主要问题是关于 $P(z_t,x_1)$ 如何计算，我们来进行推导：
$$\begin{array}{rl}P\left(x_{1:T},z_t\right)& =P\left(x_{1:t},x_{t+1:T},z_t\right)\\ & =P\left(x_{t+1:T}|x_{1:t},z_t\right)\cdot \underset{{\alpha }_t}{\underbrace{P\left(x_{1:t},z_t\right)}}\end{array}$$推导到了这里就是要对 $P(\underset{C}{\underbrace{x_{t+1:T}}}|\underset{A}{\underbrace{x_{1:t}}},\underset{B}{\underbrace{z_t}})$ 进行分析，在这个概率图模型中，符合如下结构：

根据概率图模型中提到 D-Separation 中,如下图

我们可以很简单的得出, $A\perp C|B$ 。所以, $P\left(x_{t+1:T}|x_{1:t},z_t\right)=P\left(x_{t+1:T}|z_t\right)={\beta }_t$ 。所以，我们可以得到:
$$P\left(x_{1:T},z_t\right)={\alpha }_t\cdot {\beta }_t$$那么，最终得到的就是：
$$P\left(z_t|x_{1:T}\right)\propto P\left(x_{1:T},z_t\right)={\alpha }_t{\beta }_t$$所以, 我们需要同时用到 Forward Algorithm 和 Backward Algorithm, 所以，被我们称为 Forward Backward Algorithm

5.3.3.5 Prediction

预测问题，大体上被我们分成两个方面：
$$\begin{array}{rl}公式1：P\left(z_{t+1}|x_1,\cdots ,x_t\right)& =\sum _{z_t}P\left(z_{t+1},z_t|x_1,\cdots ,x_t\right)\\ & =\sum _{z_t}\underset{P\left(z_{t+1}|z_t\right)}{\underbrace{P\left(z_{t+1}|z_t,x_1,\cdots ,x_t\right)}}\underset{\text{Filtering }}{\underbrace{P\left(z_t,x_1,\cdots ,x_t\right)}}\\ 公式2：P\left(x_{t+1}|x_1,\cdots ,x_t\right)& =\sum _{z_{t+1}}P\left(x_{t+1},z_{t+1}|x_1,\cdots ,x_t\right)\\ & =\underset{P\left(x_{t+1}|z_{t+1}\right)}{\underbrace{P\left(x_{t+1}|z_{t+1},x_1,\cdots ,x_t\right)}}\cdot \underset{For\mathrm{mula}(1)}{\underbrace{P\left(z_{t+1}|x_1,\cdots ,x_t\right)}}\end{array}$$
公式 (2) 选择从 $z_{t+1}$ 进行积分的原因是因为想利用齐次马尔科夫性质。实际上求解的过程大同小异都是缺什么就补什么。
其实，我们已经大致的介绍了 Dynamic Model 的几种主要模型，后面我们会详细的来解释线性动态系统。

6 可参考

隐马尔可夫模型HMM.
一文搞懂HMM（隐马尔可夫模型）.

版权声明：本文为CSDN博主「AI路上的小白」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/cengjing12/article/details/106592894