VRPTW：新雀优化算法NOA求解带时间窗的车辆路径问题

一、新雀优化算法NOA求解带时间窗的车辆路径问题

1.1VRPTW模型如下：

带时间窗的车辆路径问题(Vehicle Routing Problem with Time Windows, VRPTW)

1.2新雀优化算法NOA求解VRPTW

close all
clear 
clc
SearchAgents_no=30; % 种群大小
Function_name='F1'; 
Max_iteration=100; % 最大迭代次数
[lb,ub,dim,fobj]=Get_Functions_details(Function_name);
[fMin,bestX,curve]=NOA(SearchAgents_no,Max_iteration,lb,ub,dim,fobj);  %算法求解



%% 显示最终结果
Pos=ShowResult(bestX);
%% 画图
figure
plot(curve,'Color','g','linewidth',1.5)%semilogy
xlabel('迭代次数');
ylabel('路径成本');
grid on
box on
legend('NOA')
%% 保存数据
save curve curve
save bestX bestX

部分结果：

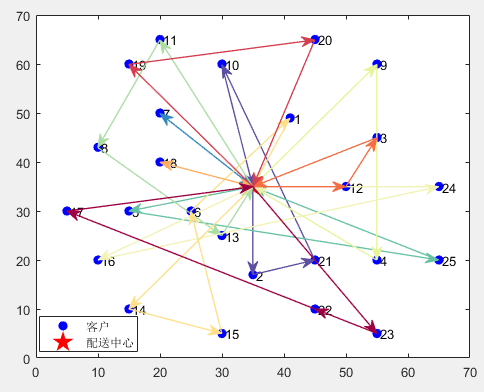
配送路线1：0->2->21->10->0 服务顾客数量：3 路径长度：96.65542 装载量：34

服务顾客2的起始时间：18.00000,结束时间：28.00000

服务顾客21的起始时间：38.44031,结束时间：48.44031

服务顾客10的起始时间：91.16033,结束时间：101.16033

抵达配送中心的时间：126.65542

配送路线2：0->7->0 服务顾客数量：1 路径长度：42.42641 装载量：5

服务顾客7的起始时间：21.21320,结束时间：31.21320

抵达配送中心的时间：52.42641

配送路线3：0->5->25->0 服务顾客数量：2 路径长度：105.14674 装载量：32

服务顾客5的起始时间：20.61553,结束时间：30.61553

服务顾客25的起始时间：81.60572,结束时间：91.60572

抵达配送中心的时间：125.14674

配送路线4：0->11->8->13->0 服务顾客数量：3 路径长度：95.79470 装载量：44

服务顾客11的起始时间：33.54102,结束时间：43.54102

服务顾客8的起始时间：67.70711,结束时间：77.70711

服务顾客13的起始时间：104.61436,结束时间：114.61436

抵达配送中心的时间：125.79470

配送路线5：0->9->4->0 服务顾客数量：2 路径长度：97.01562 装载量：35

服务顾客9的起始时间：32.01562,结束时间：42.01562

服务顾客4的起始时间：82.01562,结束时间：92.01562

抵达配送中心的时间：117.01562

配送路线6：0->16->24->0 服务顾客数量：2 路径长度：116.16353 装载量：22

服务顾客16的起始时间：29.15476,结束时间：39.15476

服务顾客24的起始时间：96.16353,结束时间：106.16353

抵达配送中心的时间：136.16353

配送路线7：0->14->15->6->1->0 服务顾客数量：4 路径长度：113.39314 装载量：41

服务顾客14的起始时间：32.01562,结束时间：42.01562

服务顾客15的起始时间：57.82701,结束时间：67.82701

服务顾客6的起始时间：93.32211,结束时间：103.32211

服务顾客1的起始时间：128.16159,结束时间：138.16159

抵达配送中心的时间：153.39314

配送路线8：0->18->0 服务顾客数量：1 路径长度：31.62278 装载量：12

服务顾客18的起始时间：15.81139,结束时间：25.81139

抵达配送中心的时间：41.62278

配送路线9：0->12->3->0 服务顾客数量：2 路径长度：48.54102 装载量：32

服务顾客12的起始时间：15.00000,结束时间：25.00000

服务顾客3的起始时间：36.18034,结束时间：46.18034

抵达配送中心的时间：68.54102

配送路线10：0->19->20->0 服务顾客数量：2 路径长度：94.05221 装载量：26

服务顾客19的起始时间：32.01562,结束时间：42.01562

服务顾客20的起始时间：72.42943,结束时间：82.42943

抵达配送中心的时间：114.05221

配送路线11：0->23->22->17->0 服务顾客数量：3 路径长度：122.37102 装载量：49

服务顾客23的起始时间：36.05551,结束时间：46.05551

服务顾客22的起始时间：57.23585,结束时间：67.23585

服务顾客17的起始时间：111.95721,结束时间：121.95721

抵达配送中心的时间：152.37102

配送路线总长度：963.18259

二、参考代码