扩增子分析|NST包-从原理到应用，教你理解群落组装机制中随机性过程、确定性过程的相对贡献（数学公式、表现性能详细介绍）

最新推荐文章于 2025-02-25 10:06:03 发布

清同趣科研

最新推荐文章于 2025-02-25 10:06:03 发布

阅读量1.1k

点赞数 23

分类专栏： R绘图基础微生物群落构建机制文章标签： r语言算法

本文链接：https://blog.csdn.net/weixin_46814750/article/details/145394818

版权

R绘图基础同时被 2 个专栏收录

12 篇文章

订阅专栏

微生物群落构建机制

7 篇文章

订阅专栏

by Tom Dingyan Zhang

一、引言

关于NST包的推出和应用已经有一段时间了。而NST到底是什么原理，有什么变式，怎么设置参数最好，并且在不同的情形下如何使用，都是有一定讲究的。最近小编精读并翻译完了宁大亮老师2019年于PNAS上介绍NST方法的文章1，总结了NST这一方法的变式和在论文中的应用。之后，小编还会总结每一种变式方法的代码实操。本文对理论方法的解读主要集中在数学公式、表现性能等方面。

二、背景介绍

了解控制生物多样性模式的群落组装机制是生态学中的一个核心问题。确定性过程是基于生态位理论且不随机的，分为非生物和生物因素，非生物因素包括外界的环境因子(温度、天气、pH、盐度等等)，而生物因素指的是互作关系(包括竞争、互利、捕食等)。通俗来说，确定性过程其实就是选择过程。相比之下，随机性过程在一定程度上无法预测。这包括随机的出生、死亡、随机的迁入迁出(扩散、迁移)以及生态漂变(生物体丰度随机变化)。经过长期的争论，目前的观念认为，确定性过程和随机过程同时控制着群落的组装。但是，确定随机性和确定性过程的相对贡献仍然比较困难。

图1 不同控制群落组装的过程示意图

在生态学领域，许多方法都用于预测确定性过程和随机过程的相对贡献。比如多变量分析、零模型(Null model，最常用，但是大部分都集中于定性方法而不是定量方法)。之前我们介绍过零模型的详细参数及R分析绘图代码，需要的同学可以跳转至基于零模型的群落确定性和随机性构建过程——R中实例计算学习。在2014年周集中老师团队的论文中2，作者们使用了选择强度(selection strength, SS∈[0, 1])来量化两种过程的相对贡献，用于预测乳化植物油对生物修复过程的影响。然而，这个方法有一个bug，有时候SS>1，因为其只考虑到，确定性过程将群落结构选择至与零期望更加相似的情况(即同质选择发挥主要作用的情况)，而忽略了异质选择导致群落结构更偏移于零期望的情况。

因此本研究将修改以前的算法bug，并在模拟群落中，将NST模型与多种方法进行比较，以评估该模型的性能。

PS：文中介绍的NST是基于丰度计算的tNST，所选用的相异性度量是非进化的。

在生态学领域，许多方法都用于预测确定性过程和随机性过程的相对贡献。比如多变量分析、零模型(Null model，最常用，但是大部分都集中于定性方法而不是定量方法)。之前我们介绍过零模型的详细参数及R分析绘图代码，需要的同学可以跳转至基于零模型的群落确定性和随机性构建过程——R中实例计算学习。在2014年周集中老师团队的论文中2，作者们使用了选择强度(selection strength, SS∈[0, 1])来量化两种过程的相对贡献，用于预测乳化植物油对生物修复过程的影响。📢然而，这个方法有一个bug，有时候SS>1，因为其只考虑到，确定性过程将群落结构选择至与零期望更加相似的情况(即同质选择发挥主要作用的情况)，而忽略了异质选择导致群落结构更偏移于零期望的情况。📢📢

因此本研究将修改以前的算法bug，并在模拟群落中，将NST模型与多种方法进行比较，以评估该模型的性能。

PS：文中介绍的NST是基于丰度计算的tNST，所选用的相异性度量是非进化的。

三、数学模型

🌟参数介绍：

元群落：即所有的群落样本组合在一块的“大群落”

Cij：第i个和第j个群落的实际相似度，范围为[0, 1]，其实就是成对距离

Dij：两群落的相异度，即1 - Cij

Eij：元群落随机打乱后得到的第i和j个群落的预期相似度。在文中要进行1000次重复，之后获得它们的均值，来表征Eij的零期望

Eij：对标于Cij的零期望，用于比较

Gij：相异度的零期望，即1 - Eij

如果确定性过程使群落结构变为与零期望更加接近，那么，Cij理应大于Eij。Cij和Eij的差异便可以用来评估随机过程在群落组装过程中的贡献，这可以称为A类选择强度。j

相应地，A类随机比例(stochasticity, ST)为：

如果确定性过程使群落结构变为与零期望差异更大，那么Cij应当小于Eij。这一情况下的选择强度可以称为B类选择强度。同理可得：

nA和nB分别为A、B情况下符合if条件的群落成对数，而n则是二者的总和。

相应地有：

之后，我们要对算出来的ST进行归一化。因为理想条件下，SS和ST为了表明确定性/随机过程在群落组装中的相对贡献，其值应在[0, 1]内，但是这两者的值不一定在这个范围，因为Eij和这一范围有很大偏差。所以，做归一化处理很有必要。将ST处理为NST，使它的范围严格在0到1之间，同时，也能够更好评估随机性过程的相对贡献。

归一化公式的参数含义：

DSS 和 TSS：SS分别在绝对的确定性过程和随机性过程下的极值(即1和0)

Eij(k)：Eij中的某一个特定值，在这里，我们要取一个特殊值，使得取到最小值。

ξ：SSij在不同条件下的广义函数。

四、表现性能：利用不同类型的模拟群落进行精准度测试

在测试开始之前，本文使用了空间隐式模型构建了群落，群落由两类简单的生物组成，一类只受确定性过程影响，而另一类受随机性过程影响，而实际的随机比率就是随机性物种在群落中的占比。

首先，使用21个模拟群落测试NST、ST、NP三者对随机比率的预测能力，其中NP指的是Sloan中性模型3,4中的“中性比例”，即群落中处在中性区域的物种比例，用这个值表征随机性过程的重要性。之前我们介绍过中性模型（NCM）的详细参数及R分析绘图代码，需要的同学可以跳转至中性模型（NCM）在R中快速复现学习。

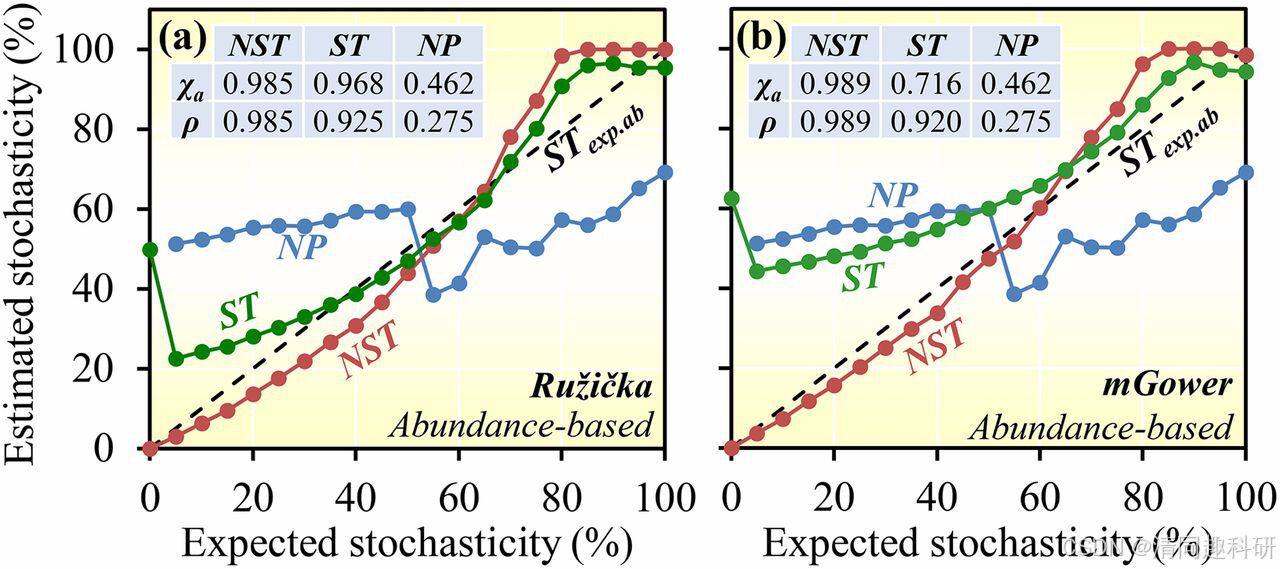
图2 NST对比ST、NP的预测性能

(a) 基于Ruzicka距离指数；(b) 基于mGower距离指数

根据图片结果和补充资料，可见NST在预测的准度和精度上最优，其次是ST，最后到NP。

选用不同基于物种出现率的度量(如Jaccard)，NST都表现出>0.99的高准度和高精度。无论是相对差值度量(Ruzicka, Bray–Curtis, Kulczynski, Chao)，还是平均相对差值度量(mGower)，还是绝对差值度量(Manhattan)等。然而NST在平方和度量中显示出的预测结果不佳。

作者在文段最后下了结论，根据综合性能，推荐读者使用Jaccard或Ruzicka度量去进行NST分析。

由于群落的多样性模式和组装规律一定程度上依赖于群落尺度，因此本研究还通过空间显式模型，以分层方式构建了不同尺度的群落，来模拟不同的空间大小。包括地块(plot)、场地(site)、地域(region)、洲(continent)、全球(global)。

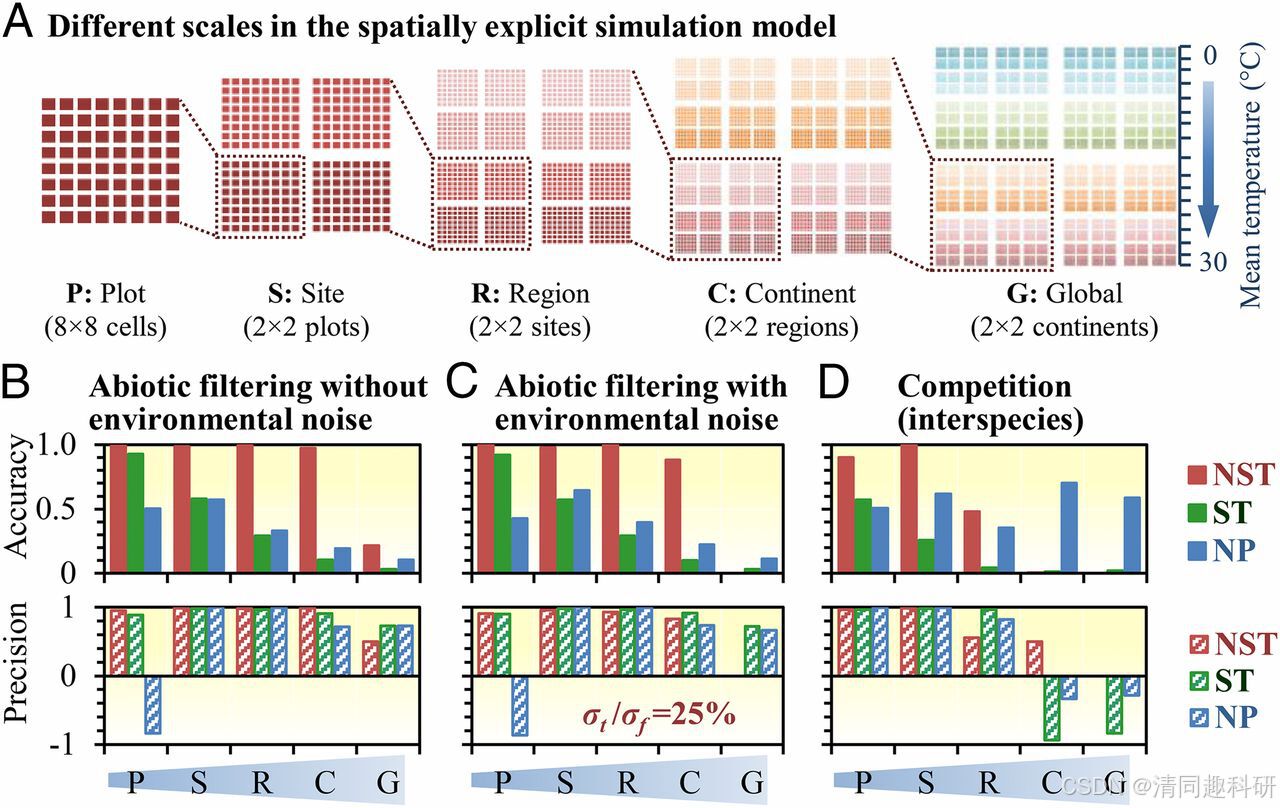
图3 测试示意图和模型在不同情形下的预测性能

(B) 无环境噪音；(C) 有25%噪音；(D) 考虑种间竞争但去噪

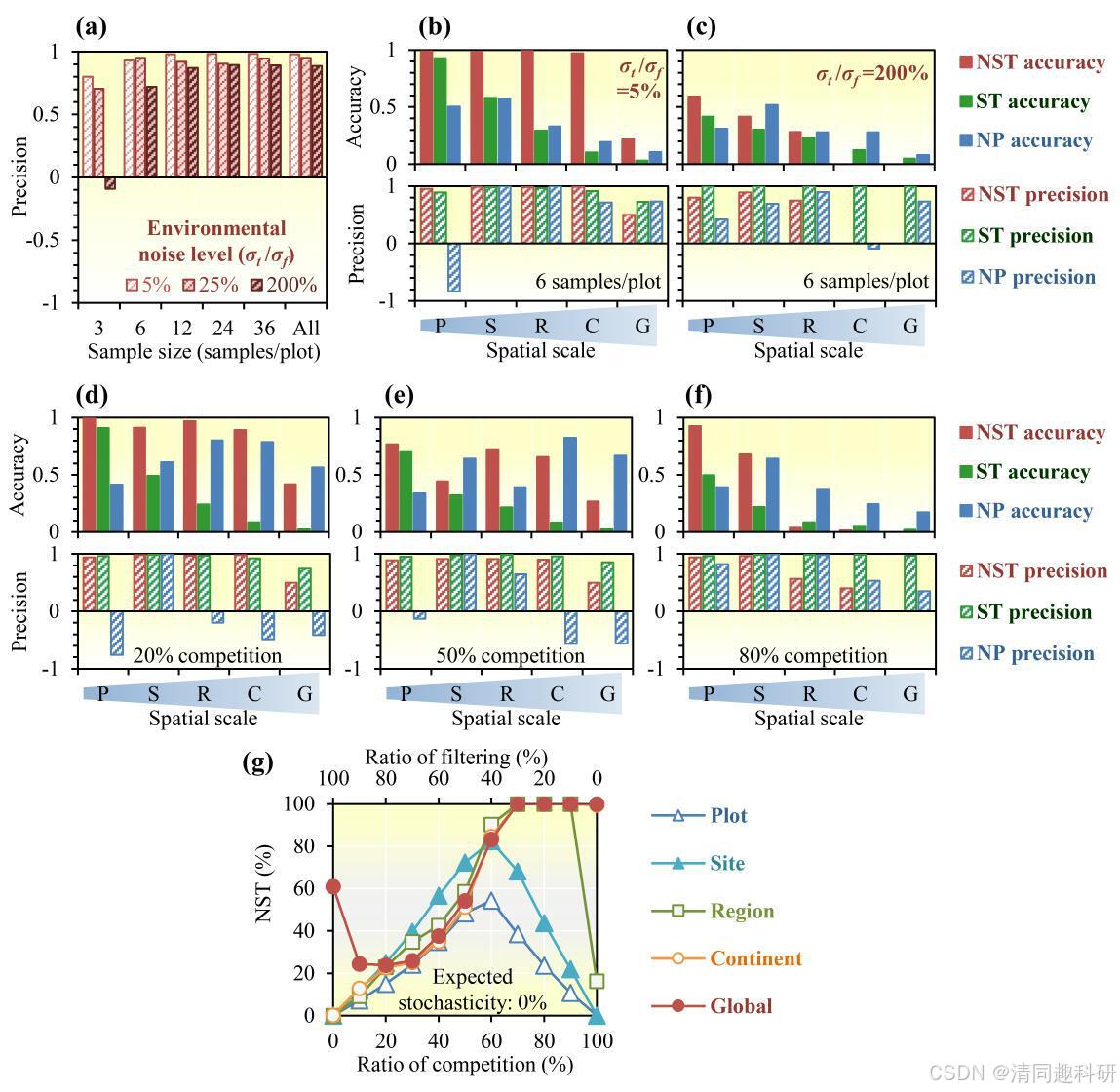
图4 补充资料测试结果

根据图片显示的结果，我们可以发现NST在无环境噪音或噪音低的情况下在低于全球尺度时具有优秀的准度和精度。而在有种间竞争的情况下，其仅适用于较小尺度。同时根据补充资料，当参与分析的样本数≤6时，NST的预测性能并不佳。因此，要保证参与NST分析的样本数量是足够大的，不能太小。同时，通过图4(g)可以得到，当种间竞争占据主导作用时，NST会高估随机性过程的比率(尽管实际上随机性过程占比为0%)。以及，从所有的图来看，当尺度扩张到全球时，NST的预测能力会急剧下降。

五、参考文献

1. Ning, D., Deng, Y., Tiedje, J. M. & Zhou, J. A general framework for quantitatively assessing ecological stochasticity. Proc. Natl. Acad. Sci. 116, 16892–16898 (2019).

2. Zhou, J. et al. Stochasticity, succession, and environmental perturbations in a fluidic ecosystem. Proc. Natl. Acad. Sci. 111, (2014).

3. Sloan, W. T. et al. Quantifying the roles of immigration and chance in shaping prokaryote community structure. Environ. Microbiol. 8, 732–740 (2006).

4. Burns, A. R. et al. Contribution of neutral processes to the assembly of gut microbial communities in the zebrafish over host development. ISME J. 10, 655–664 (2015).