车辆运动学模型推导【一看就会】【四轮车模型】

提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档

---

前言

先看上一章【自行车模型】

有了上一篇【自行车模型】的基础，这章咱们进一步，来看【四轮车模型】。
先看我复制过来的图：

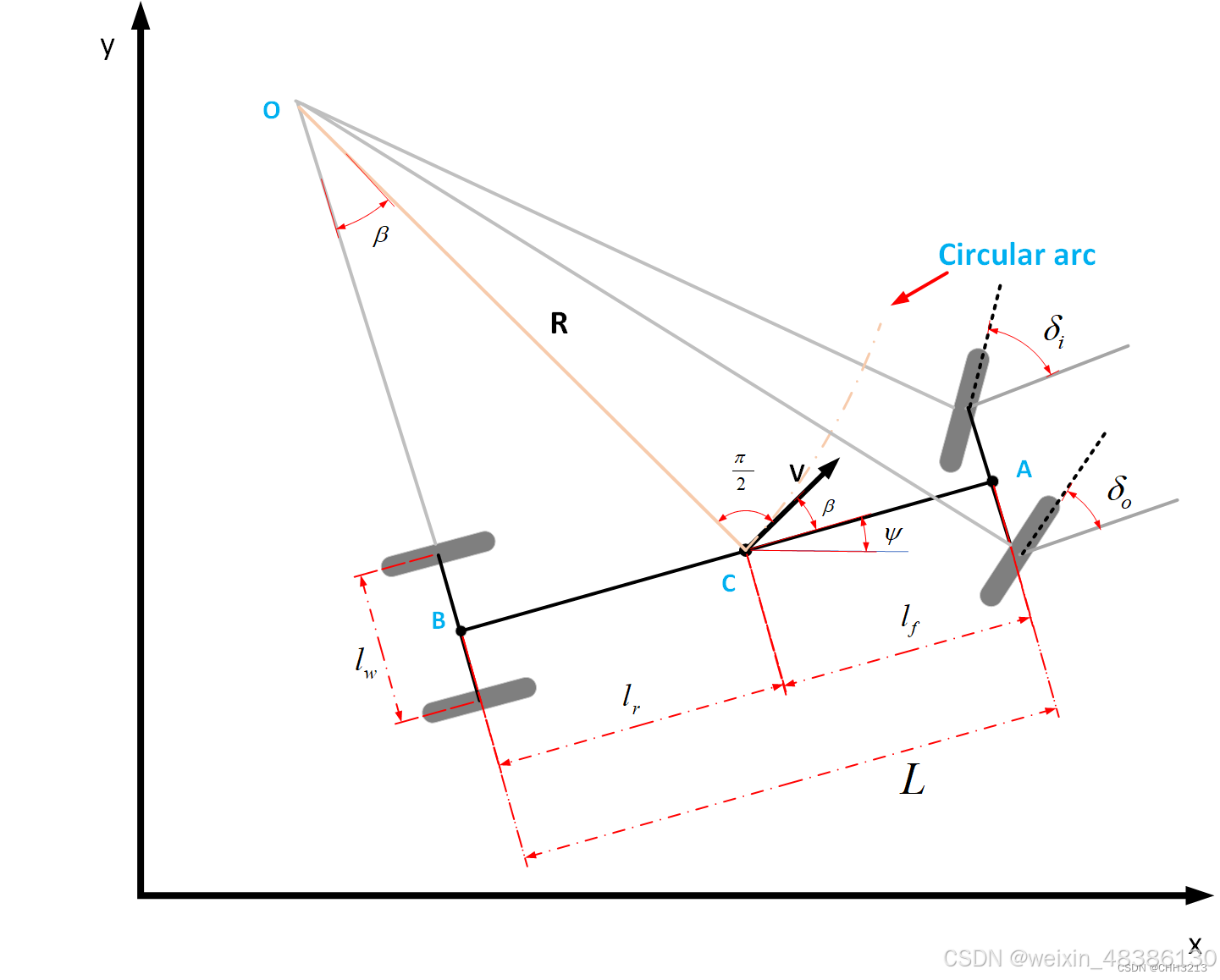
图片来源：https://blog.csdn.net/weixin_42301220/article/details/124747072
我们还是从输入输出等出发，结合上一章推导出来的公式，进行这部分推导。
上面这个图你现在看也看不出来啥，跟着我往下走，公式里面的字母再来看这个图对应。

---

``

一、【输入】【输出】【已知量】？

和上一章一样：
1.汽车速度：V；
2.前内轮与车辆夹角：δi；
3.前外轮与车辆夹角：δo；
【已知量】有三个：
1.前车轮与车辆中心的距离：Lf；
2.后车轮与车辆中心的距离：Lr；
3.前轮两个轮子的轮距：Lw；
【输出】也有三个：
1.汽车在全局坐标系下【X方向速度】：Vx；
2.汽车在全局坐标系下【Y方向速度】：Vy；
3.汽车【角速度】：ω；

你一定会看到，没有后轮的夹角了，替代的是前轮变成了两个轮子的分别夹角。（你要是没看到，证明你光看了没进脑子，我也经常出现，所以才开始写这些内容。）
这是因为汽车后轮是固定的没有转向角。（比亚迪的仰望后轮也是固定的哈，用的差速。）

明确输入和输出了，接下来就随着我开始推导。

再次强调一遍：
你的目标，用【输入】表达【输出】。
除了两个【已知量】之外，不能再有别的字母。
面试要问你推导过程，你就先画图，再把输入输出写下来，再推导。
接下来看推导。

##一定时刻要记得【输入】【输出】和【已知量】。

二、推导步骤

1.先复习上一章的公式，并开始简化

代码如下（示例）：

Vx=V*cos（β+Ψ）；
Vy=V*sin（β+Ψ）；
ω=V/R；
其中：
Ψ的微分ψ=ω；
R = (Lf + Lr) / cos(β)*[tan(δf) - tan(δr)]	    （10）
β = arctan{ [tan(δf) * Lr+ tan(δr)* Lf]/(Lf+Lr)}		（13）

【四轮车模型】是以【自行车模型】为基础的，所以
先不着急整【四轮车模型】，咱们先简化根据条件继续简化上面的式子。

2.开始简化

看上面的公式里，δf是前轮，δr是后轮，四轮车模型中的后轮夹角为0.
则R和β可以简化：
R = (Lf + Lr) / cos(β)*tan(δf)] （10）
β = arctan{ [tan(δf) * Lr]/(Lf+Lr)} （13）

然后咱们继续简化，
这时【神奇】的就来了，β直接等于0，这你敢相信？
其他资料里给出的理由，是由于轴距（前后轮距离）远远小于车辆转弯半径R，然后就β=0了。

咱们看一下自行车模型的图：

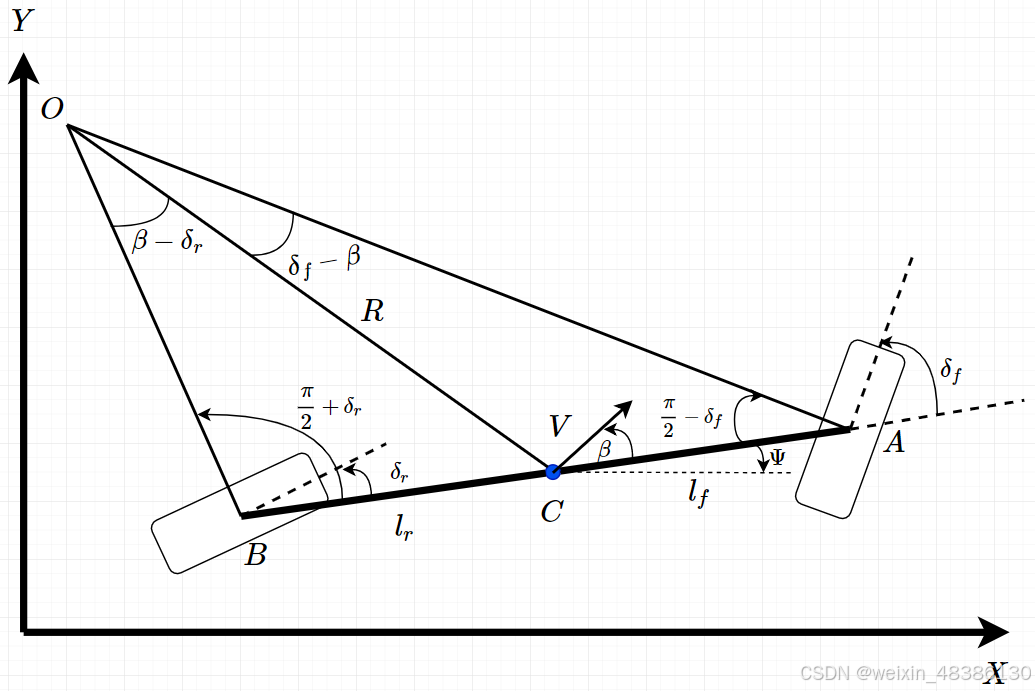
图片来源：https://blog.csdn.net/liumengxie/article/details/129899469

首先是后轮无夹角，然后把R变长，车身变短，Lr也跟着变短，是不是R快和后轮垂直的线重叠了，β是不是接近于0了。
反正我就是这么说服自己的。

就这么简化了。
R = (Lf + Lr) / tan(δf) （10）
β = 0 （13）

然后又【神奇】的来了，因为δf很小，所以：
tan(δf) ≈ δf
卧槽，凭啥δf很小呀，汽车转向就不能大一点？
这个我就没法解释了，只能把它当作简化的过程了，兄弟们要是能解释清楚的说一下。

然后上面的式子就变成了：
R = (Lf + Lr) / δf （10）
β = 0 （13）

这里要记住，δf的前轮转向角，是等效【自行车模型】后的结果。
咱们是【四轮车模型】，前轮转向角有两个：
2.前内轮与车辆夹角：δi；
3.前外轮与车辆夹角：δo；
你可别问我为啥前轮两个轮子角度不一样，自己去看一下阿克曼转向的知识。

然后，咱们就需要用δf和【已知量】把前轮两个轮子的角度表示出来：
错！
是根据
R = (Lf + Lr) / δf 得到
δf =(Lf + Lr)/R
然后直接不过脑子的替换：
δi =(Lf + Lr)/(R+Lw/2)
δo =(Lf + Lr)/(R-Lw/2)
这又是凭啥呀。
其实是相当于把前内轮和前外轮，和对应的后轮连接，然后各自做了一套【自行车模型】，然后再推导过来的。
怎么，你以为δf直接是前面两个轮子角度的和的一半？再复习以下阿克曼转向去吧。

然后这个时候才有了前轮平均转向角：
δ=(δi+δo)/2=
（这个公式我不知道怎么打）
然后里面的Lw比R小很多，然后公式就能简化：
δ=(δi+δo)/2=(Lf + Lr)/R

咱们再返回来看【自行车模型】的公式：
Vx=Vcos（β+Ψ）；
Vy=Vsin（β+Ψ）；
ω=V/R；
其中：
Ψ的微分ψ=ω；
R = (Lf + Lr) / cos(β)[tan(δf) - tan(δr)] （10）
β = arctan{ [tan(δf) * Lr+ tan(δr) Lf]/(Lf+Lr)} （13）

把咱们上面简化的结果给代进去：
Vx=Vcos（Ψ）；
Vy=Vsin（Ψ）；
ω=V/R；
其中：
Ψ的微分ψ=ω；
R = (Lf + Lr) / tan(δf)
β = 0
其中 δf使用平均转向代替：
δf=δ=(δi+δo)/2

这里需要注意的是，虽然上面推导过程中为了简化为下一步，其中有tan(δf) =δf这些简化，但是在最后的公式中，可以保留，减小误差

里面有些地方我也觉得不合理，等之后了解清楚了我再回来解释。

注意：其中有很多做了近似的运算，会不断造成误差，主要是方便最后的简化计算，实际编程过程中可以不近似，让计算机自己算。

总结

【四轮车模型】是完全根据【自行车模型】推导出来的，所以也只能用于低速。