几种简单的自动驾驶控制算法【一看就会】【MPC，NMPC,LQR,PID】

最新推荐文章于 2025-03-07 09:29:04 发布

不断学习加努力

最新推荐文章于 2025-03-07 09:29:04 发布

阅读量4.4k

点赞数 60

文章标签：自动驾驶人工智能机器学习

本文链接：https://blog.csdn.net/weixin_48386130/article/details/142924438

版权

提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档

文章目录

前言
一、输入输出
一、PID
二、LQR
- 算法介绍
三、MPC
四、NMPC
总结

前言

这里光讲控制算法，下一篇文章再讲在自动驾驶中的运用

好久不见，之前讲了车辆运动学和动力学模型，让我们对需要控制的车辆有了数学模型，今天我们讲一下几种在自动驾驶领域常见的控制算法，为下一步我们控制汽车进行准备。

本次主要讲的控制算法有四种，分别是PID,LQR,MPC和NMPC

其中NMPC是我研究生课题做过一部分，但好像实际中没什么人用。

其他三种都很常见，是在自动驾驶领域还有别的机器人领域常见的基础控制算法。

里面没有代码，想复制的先不用进来，等我之后有空了写了给贴进来。

一、输入输出

在讲控制算法之前，我们还是先从【输入】【输出】开始讲

控制算法中，输入的叫【期望值】也就是你希望它是怎么一个值，输出是【实际值】

这里给大家举个例子，就像你骑自行车，你希望能一直压着白线走，但实际上歪歪扭扭，这就是你的输入输出。

而控制算法，就是为了让【实际值】能尽可能地逼近【期望值】

那为什么【输入】和【输出】不相等呢？
因为有【误差】，带来【误差】的原因是多种多样的，比如执行器精度不够，就是你给他输入了1m，它实际走了0.999m；还有像是延迟等。

而所有的控制算法，就是为了消除这个误差而整的。

到这里肯定有人已经迷糊了。
为什么刚输入就会有个输出来做误差呢？

我来给大家解释一下，比如汽车准备开始走了，你有个预期的速度是30km/h，你先踩一脚油门，这是因为汽车一开始还没有动，所以速度距离你的【期望值】的【误差】就是30km/h，然后因为有了速度，【误差】变为20km/h，你就踩了第二次油门，到第五次的时候，你准备踩油门，却发现此时速度已经是29.9km/h了，于是你就小踩一下，但是没想到速度变成30.1km/h了，此时你就需要松开油门。前面这一系列的操作，就是你在根据你的【期望值】去调整【实际值】，要是新司机呢，就容易风琴脚，也就是油门一深一浅，老司机就能一步到位，很平顺，并且不会出现超调，让人坐着很舒服。这个反应到控制系统上，就是老司机控制的比新司机好。

大家带着这个思想，我们进行以下的控制算法讲解。

一、PID

先讲大家最熟悉的，也是在各个控制系统中最常用的，几乎所有的机器人控制和车辆控制都离不了它。

先看图，最基础的PID控制算法：
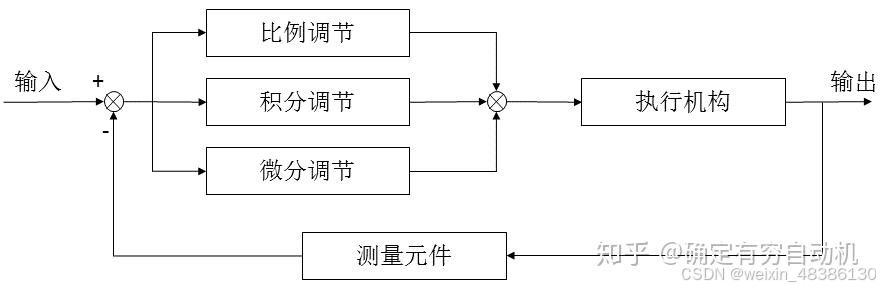
在这里插入图片描述
图片来源：https://zhuanlan.zhihu.com/p/39573490

如图所示：
PID是比例，积分，微分系统，三个字母就是代表这三个。
也就是说PID就是这三个系统的耦合系统。
听不懂正常，这纯理论，没法过脑子，记着就行。
接下来看我的解释。

咱们先继续看图，你看他们比例，积分，微分系统是并列，就是【误差】要分别经过这三个系统，然后再加起来。

给出PID系统的数学模型：
在这里插入图片描述
图片来源：https://zhuanlan.zhihu.com/p/39573490

其中U(t)就是PID控制系统的输出，用这个输出来控制之后的执行器。
err(t)就是【期望值】和【实际值】的误差，然后等式里面kp就是比例控制器，括号里面的第二项就是积分控制器，第三项就是微分控制器。
有人会问：比例控制器不是并列的吗，为什么现在在最外面了？
也可以放进里面。

然后我们分别讲【比例】【积分】【微分】的作用。

1.比例

比例很好理解，把误差乘以个系数，到时候误差要是嫌大了就乘个小的系数，误差要是嫌小了就乘个大的系数。（根据最上面的油门控制车速，理解为什么对误差的要求不一样。）

很明显，这个控制是纯线性的。

比例控制的特性：
比例系数小，那就相应的慢，比例系数大，控制的快但是震荡大。

到这里就又需要解释一下这句话了：
还是用踩油门控制车速的例子，你想到快点到30km/h，是不是得用力踩油门，是加速很快，但是很容易踩过去，然后你就得赶紧松开，或者还得踩点刹车，你要是踩刹车也很大力度的话，就又小了，然后你就一会油门一会刹车，速度就来回的飘。这个放在系统中就是震荡大。
但你要是慢慢踩油门，是稳定并且好控制，但等你快到家了，速度还没加起来，几公里的路程你开了一个小时。这个放在系统中就是响应慢。

那又想反应快，又不想有震荡怎么办？
那就需要我们的【微分】系统出场
（虽然PID，但是我们讲完P先讲D）

2.微分

微分系统的作用就是为了抑制震荡。
我们先给出微分系统的模型：
在这里插入图片描述

图片来源：https://blog.csdn.net/weixin_44562404/article/details/107718808
大家看等式右边，Kp就是上面的比例系数，Td是微分时间常数。

其实最让大家疑惑的是后面那个微分公式。
后面那个微分其实是【先前一段时间内的偏差变化率】。
前面的偏差变化率太大，就调整Td参数变小，要是变化率太小，就给个大的Td参数。
很多人到这里就看出来了，微分调节是一个根据旧数据的提前调节。

Td越大，则抑制震荡的能力越强。
到这里肯定有人问了，Td越大不是偏差【变化率】越大吗，怎么反而抑制震荡的能力越强了？
这个我复制一下别的博客里的话来解释一下，或者你只需要列几个速度值自己看一下也可以：

现在让当前的速度值为90，目标值为100，Bias=10。现在是为了接近目标值，所以D项的结果是增加PWM。现在增加后的速度变成了105，Bias=-5,Last_Bias=10，Bias-Last_Bias=-15，如果增加后的速度为110，Bias=-10，Last_Bias=10，Bias-Last_Bias=-20，D项的计算结果是为了减小PWM，快速抑制住PWM的过量增加，超过目标值越多，那么抑制能力越厉害。
原文链接：https://blog.csdn.net/a2001444/article/details/118053894

从这里就理解，积分变化Kp是直接调节【偏差】的大小，会产生震荡；而微分系统的参数Td则是调节【偏差】变化率的大小，可以抑制震荡。

但是光用【比例】和【微分】调节就会出现一种情况：【期望值】和【实际值】还有【偏差】，但是【偏差】太小。【偏差】小，那【比例系统】就会减小比例系数，就像快到目标速度了就得放缓油门；但是此时震荡也很小，【偏差】变化率为0，那【微分系统】就也不会工作。
这种情况，就会越临近【目标值】，变化的越慢，会在很长时间内达不到【目标值】。
于是，需要解决【目标值】和【实际值】的偏差，也就是【静态偏差】，所以就有了积分。

3.积分

先给出模型：
在这里插入图片描述
图片来源：https://blog.csdn.net/weixin_44562404/article/details/107718808

看公式里面的，Kp还是比例系数，Ti是积分常数，后面是对之前时间的偏差进行积分。

积分系统的作用是消除静态偏差。

然后我来解释这部分的积分信息：
首先是积分常数Ti，它越大，1/Ti越小，1/Ti越小，积分控制器的作用越小，消除静态偏差的时间就越长，相应就越慢。

PID结束
通过上面，大家会看出，比例P是基础，I和D是调节，所以就存在PI和PD控制器，各有缺点。
PID控制器的调节参数就是指调整【比例系数】Kp，【积分系数】Ti和【微分系数】Td。

根据这三部分的各种性质会产生很多优化方案，之后我再进行补充。

二、LQR

先说一下，LQR一定要一次性全看完，搞懂，至少留两个小时的空余时间来看以下这部分，否则就先看后面的MPC和NMPC。

这是我认为最难理解的基础算法，但为啥难理解，我最后会解释。

上面PID说完了，我们来说另外一种常用的算法——LQR。

LQR相对于PID理解起来就难很多了。

但是万变不离其宗，所有控制算法的目的都是一样的，都是要又好又快地减小【偏差】。这个在这片文章的最上面有写，大家一定要记住。

然后带着这个思想，让我们来看一下LQR控制器是如何又快又好地减小【偏差】的。

LQR是状态反馈控制，这个大家在很多博客中都看到过。但是大概率看不太懂，我们在此做出解释。

像是PID，如果要控制【速度】，那输入输出就都是速度，然后放进PID算法中进行运算，并且是单输入单输出；如果要是想同时控制【转向】，那就需要再起一套PID，然后把角度的【期望值】【实际值】放进去进行计算。

但是LQR不同，【输入】【输出】没法提前解释，只能大家随着我下面写的来看。所以大家一定要一次性全看完，否则很难理解。

算法介绍

先看一眼算法框图：
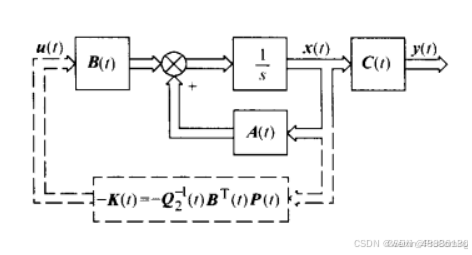
在这里插入图片描述
图片来源：https://blog.csdn.net/ProComing/article/details/140405262

图片来源：https://zhuanlan.zhihu.com/p/363033191
肯定看不懂哈，继续和我往下走。
再看一眼LQR模型公式：

图片来源：https://blog.csdn.net/weixin_43487974/article/details/127195643
到这里也还是肯定看不懂哈，不着急。

我们先看两个公式，第一个公式叫状态方程，第二个公式叫输出方程，其中y就是最后系统的输出，但是这个【系统输出】大家不要以为就是我们想得到的东西，我们先继续往后看。

我们再继续看输出公式中的内容，大写的都是系数矩阵，这个等会说。
小写字母有两个，其中x是系统的状态向量，u是系统的控制输入。

到这里也完全看不懂也非常正常，不要着急，我来用实际案例继续解释。

假设我们有一辆自动驾驶汽车，需要通过控制【加速度】和【方向盘角度】来保持在【道路的中央】并以【恒定速度】行驶。

那这里面的【状态向量】x是什么呢？
是车辆目前的状态，这个状态需要与我们的【预期目标】：【道路的中央】和【恒定速度】相关，有很多种答案，这个需要自己根据实际情况去选择，我们选择其中一种：
在这里插入图片描述
那【控制输入】u是什么呢？
就是我题目种想控制的量：【加速度】和【方向盘角度】

那输出方程的y在这个例子中指什么呢？
在这里插入图片描述
是不是很意外，对，这个例子中输出和状态是一样的。

到这里就很迷糊了，那状态都已经是输出了，为啥要写这个这么费劲？
少年，你还记得反馈吗，还记得PID输出绕回来作为反馈吗。
这个是一个道理。
到这里就有人问了，那【状态反馈】就是【输出反馈】吗？
也不一样，我来给你解释：
这个例子里是【输出】刚好等于【状态】，这是为了大家方便理解【状态反馈】，但实际上，【状态】要比输出要多，就像这个例子中的状态，它还可能有【变速器温度】【油箱油量】等等，说白了，【状态】是当前传感器接收到的量，有时候和【输出】一样，有时候能包含【输出】，有时候就和输出没关系，我用这个例子完全是为了方便讲解和让大家理解【输出反馈】。

到了这里是不是就有些理解了，如果还是不能太理解，那肯定是我说的不清楚，之后我再补充或者修改。

我们到此就将第二个输出方程的三个变量给说完了，还有两个大写字母：
C是输出矩阵，描述状态变量和输出之间的关系；
D 是直接传递矩阵，描述控制输入和输出之间的关系。
这两个没什么可解释的，就是叫这个名字，需要说的是它俩怎么得到和计算。
但是这部分我们先稍微等一下再说。

我们先说第一个状态方程，还是有三个小写字母和两个大写字母。
x已经讲过了，就是【状态向量】。
等式左边带点的x，就是x的时间导数，也就是【状态向量】的变化率。
u也说过了，就是【控制输入】
A是状态矩阵，描述状态变量之间的演化关系；
B是输入矩阵，描述控制输入对状态变量的影响；
大写字母就记住是啥就行。

这个时候大家应该会有个大概的印象了，并且肯定有很多疑问，我们挨个解释：
1.我们要的不就是【加速度】和【方向盘角度】吗，怎么当输入了？
这个就需要解释一下，在这里插入图片描述
是【控制输入】，不是像PID中我们给的【输入】，虽然名字里带【输入】，但这个是抽象的系统的【控制输入】，实际上就是我们这个系统最后要的东西。
为啥非要叫这个名字我也不清楚，在我弄懂之前，因为【控制输入】这个名字，让我对LQR一直理解不了。
那LQR【输出】又是什么呢，这个【输出】不是我们要的输出，它是用来和我们的【期望目标】做对比的，也就是我们心中最终的目标：保持在【道路的中央】并以【恒定速度】行驶。
我们把在这里插入图片描述和【道路中央】的坐标还有【恒定速度】的速度做对比，来衡量我们这个系统好坏，怎么评价好坏呢，要是不好的话调整哪个参数呢？

要调整哪个参数呢？
可不是ABCD，这四个字母是系统模型，也就是几个【状态】【系统输入】和【输出】的关系，这个咱们最后再解释。

要调整的参数我们需要看：
在这里插入图片描述这张图，在我们最上面放着，还一直没讲，大家看一下，上面哪个公式就是咱们的状态方程，但是下面还有一个-K，然后【状态】和这个-K乘了一下，作为【系统输入】给反馈上去了。

这里是不是又懵了，要理解这个图，咱们先完全不考虑刚才讲了半天的输出方程。
咱们把这个就当作一个完整的系统。
输入经过在这里插入图片描述这个方程，然后变成输出x，输出x再反馈回来，并乘-K作为输入。这个是不是能有些许的理解。
那就有个关系：
u=-Kx
再返回咱们那个例子中，就是：
=-K
（有点难看将就一下哈）
这个K就叫控制器增益矩阵。
叫什么不重要，知道它是什么最重要。

到这里，我们还是不知道评估好坏的方法，也不知道这个怎么优化。
有意思的来了，先看下面这个：
在这里插入图片描述
这他妈又是啥！
这叫成本函数或者性能指标。
叫什么不重要，重要的是干什么用的。
它！就是咱们评价整个系统好不好的指标！也就是咱们讲了半天，一直没出现的，整个系统的目标。

其中：
Q是对【状态向量】x的加权矩阵，表示我们对不同状态的重视程度；
R是对【控制输入】u的加权矩阵，表示我们对控制输入的成本的重视程度。

对这个理解，一定要结合我们例子里的：
=-K* 在这里插入图片描述
通过调整Q和R的值，我们可以平衡系统的状态和控制输入之间的权衡。当我们想要更加重视状态时，增加相应状态的Q值；当我们想要更加节约控制能量时，增加相应控制输入的R值。

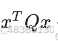
在这里插入图片描述
叫【状态偏差成本】。
叫【控制输入成本】。
我们结合上面的例子来说明一下：
状态偏差成本：假设你想让自动驾驶汽车保持在车道中心并保持恒定速度。如果汽车偏离车道或速度与期望值有较大差距，LQR会将其视为较大的状态偏差，这会导致较高的状态成本。
控制输入成本：如果你希望汽车回到车道中心，可以通过转动方向盘和加速/减速来实现，但如果你频繁地剧烈调整方向盘或加速器，会增加控制输入的成本。因此，LQR不仅会尽量减小状态偏差，还会尽量减少控制输入的幅度或频率。

整个LQR系统的目标，在此时呼之欲出：找到一个最优的控制器增益矩阵K，使得成本函数J最小化。

到这里又不理解了，K和成本函数J有鸡毛关系啊。
我来解释一下：
我们的目标就是为了让成本函数J尽可能小，你们看公式中，成本函数是前后两个的和，让成本函数尽可能小，也就是让前后【状态偏差成本】和【控制输入成本】都尽可能小，这就是一个【最小二乘优化问题】。
为什么【成本函数】是要让【状态偏差成本】和【控制输入成本】尽可能小呢，这里解释一下：
尽量减小状态偏差：让系统的状态𝑥(𝑡)尽可能接近目标状态（通常是零状态）。
尽量减少控制输入的代价：让控制输入𝑢(𝑡) 尽可能小，以避免过度操控。

我还没解释K和J的关系哈，不着急，我下面说：
K 控制了如何根据当前的系统状态𝑥(𝑡) 生成最优的控制输入𝑢(t)。
K 是在给定Q 和 R 的前提下，通过LQR算法来计算的。

Q和R这个权重不是系统给的，是你给定义的，得看你对不同【状态】和【控制输入】的重视程度。

然后【状态】是根据传感器得到的，根据【状态】*K就能得到【系统输入】，然后在带进【成本函数】J中，就是一个只有一个变量K的最小二乘问题。

【状态】是传感器得到的！不用你算！

到了这里，我们终于终于把这个LQR给讲完了。

为啥你之前一直不懂LQR，是因为它【系统输入】不是咱们理解的输入，是咱们想要得到的东西，这个太具有困惑性了，所以很多人一开始就不知道【输入】和【输出】是啥，查半天也理解不了。

再返回头去看输入方程，它可以没有，可以直接用【状态】衡量。

前面如果有不通的不顺的，前后感觉理解不了的，不要怀疑是自己的理解，一定是我写的不清楚，我之后再返回头来改改。

要是你能看懂并且理解，那你是真厉害了。

三、MPC

如果你从LQR而来，那你终于能喘口气，让我们理解一下比较好理解的MPC。
MPC叫模型预测控制。叫什么不重要。
它用来干啥的，是通过模型来预测系统在某一未来时间段内的表现来进行优化控制。常用来做无人驾驶中的路径跟踪。

看不懂，没关系，纯理论肯定看不懂。

我们还是根据【输入】和【输出】来看，如果你能理解了上面的LQR，那你这部分会比较好理解，如果还没看上面的LQR，那就随着我往下看。

我们首先来看一下MPC的模型公式（状态方程）：
在这里插入图片描述

图片来源：https://blog.csdn.net/w_w_y/article/details/123917212

跟着这个方程，我们还是从【输入】【输出】开始讲。
等式左边x(k+1)就是系统的【输出】
等式右边u(k)就是当前系统的【输入】
等式右边x(k)是当前的【状态量】

还是看不懂也没关系，先举个简单点的例子：
让汽车在5秒内从静止状态加速到60公里/小时，并保持匀速行驶。
要用MPC实现以上的内容，此时：
【输出】x(k+1)就是车辆下一时刻的速度；
【输入】u(k)就是我们给车辆的加速度；
【状态量】x(k)就是当前车辆的速度；

根据速度和加速度的关系，有：
x(k+1)=x(k)+u(k)*t
以上这个式子就是【预测模型】

你这个时候想一下自己想得到什么呢？
没错，是系统的【输入】，也就是给车辆的加速度，就是自己踩的油门大小，这是自己能控制的量。
当前的【状态】也就是车辆当前的速度用传感器获取。
【输出】也就是下一时刻的速度还没算出来，也是未知的，所以目前这个式子求不出来。

那让我们继续往下讲。
把上面式子的【输出】作为预测到的【状态量】，再计算下下一时刻：
x(k+2)=Ax(k+1)+Bu(k+1)

然后以此类推，往下列式子，可以列30个，也可以列50个。
不停往下类推列式子，就叫【滚动预测】。
这30个或者50个式子，就是30或50步。如果一个控制周期是3s，那对应的【步长】就是0.1s或者50/3s。

那咱们列出了这么多式子，还是没法求啊。

这个时候就需要回到我们的题目，【目标】是60km/h，假设你打算在这一个控制周期就实现，那最后的x(k+30)就是60km/h。
以此往前推。
为什么有这么要列这么多式子呢，一步实现不久行了吗？
因为我们的加速度不可能那么大，这也就引入了MPC的另外一个要素：【约束】。
放在我们这个例子里就是加速度的最大值。

这个例子比较简单，但是你先不要在脑子里直接求解哈，先跟着我继续走，理解MPC。
到这里，还是算不出我们要的【输入】也就是控制量加速度。
因为没有一个【评估】。

让我们再返回头去看条件，我们的目标只有一个，就是达到【目标速度】，每个时刻的【目标】都是它。
那每个时刻的【输出偏差】就有了，也就是x(k+1)-60km/h
我们预测了30步，也就有30个【输出偏差】，让这些【输出偏差】的和最小，就是我们的【优化】。
求解这个【优化问题】，就会得到最优【控制量】，也就是我们的【输入】加速度。
这个例子中的优化函数：
在这里插入图片描述
N：预测步数，也就是我们定的30步或者50步。
v：速度
a：加速度
λ：加速度权重。正则化系数，用于权衡控制输入（加速度）和跟踪误差之间的平衡。
整个优化目标就是让这个方程在【约束】下值最小。

而以上这一步就叫做【滚动优化】。

得到了这么多加速度，我们仅使用下一时刻的加速度，也就是a(k)。

然后在下一时刻到临时，再进行同样的步骤，用下一时刻的【状态量】进行反馈优化，再指导下下步的动作。
这个就叫做【反馈矫正】。

于是MPC的三大要素【预测模型】【滚动优化】【反馈矫正】就解释结束。

如果有不清楚的我再回头进行修改。因为写到MPC的时候我已经有些疲倦了。

四、NMPC

NMPC比MPC多的这个N，指的是非线性，于是全程就叫做非线性模型预测控制。
这部分需要你先理解了MPC再来看，我会写的比较简单。

非线性主要体现在两方面：
【预测模型】的非线性和【优化函数】的非线性。

在MPC中我们讲了一个非常简单的例子，速度和加速度，是线性的，但在实际工况中，【预测模型】经常是非线性的，我们再讲个例子：
（这个例子还是蛮难的，大家慢慢看）
假设我们有一架四旋翼无人机，目标是在三维空间中跟踪一条给定的轨迹（如飞行沿着某条曲线）。无人机的动力学模型是非线性的，这使得它难以用线性控制器（如MPC控制）精确控制。我们使用NMPC来解决这个问题。

【预测模型】是非线性的：
无人机的状态包括：位置𝑝(𝑡)=[𝑥(𝑡),𝑦(𝑡),𝑧(𝑡)]p(t)=[x(t),y(t),z(t)]、速度𝑣(𝑡)=[𝑣𝑥(𝑡),𝑣𝑦(𝑡),𝑣𝑧(𝑡)]姿态角度（俯仰、偏航、滚转）和角速度。这些状态随时间演变的动力学模型为非线性关系，受力包括重力、推力、旋翼提供的控制力矩等。
状态方程可以简化为：
在这里插入图片描述
其中xk是无人机当前的状态，包括位置、速度和姿态。
uk是当前的控制输入，包括推力和舵机角度。