最优控制学习笔记2----泛函

Sunshing15

已于 2023-01-09 13:42:19 修改

阅读量727

点赞数

分类专栏：最优控制文章标签：学习

于 2023-01-08 20:05:48 首次发布

本文链接：https://blog.csdn.net/weixin_52721512/article/details/127974437

版权

最优控制专栏收录该内容

9 篇文章 0 订阅

订阅专栏

文章目录

泛函

泛函

泛函定义

对于某一类函数集合 ${x(t)\}$ 中的每一个函数 $x (t)$ , 在映射关系 $J$ 下均有一个确定的数与之对应，则称 $J$ 为依赖于函数 $x (t)$ 的泛函，记作 $J = J [x (.)] = J [x (t)]$
注：泛函与函数的区别
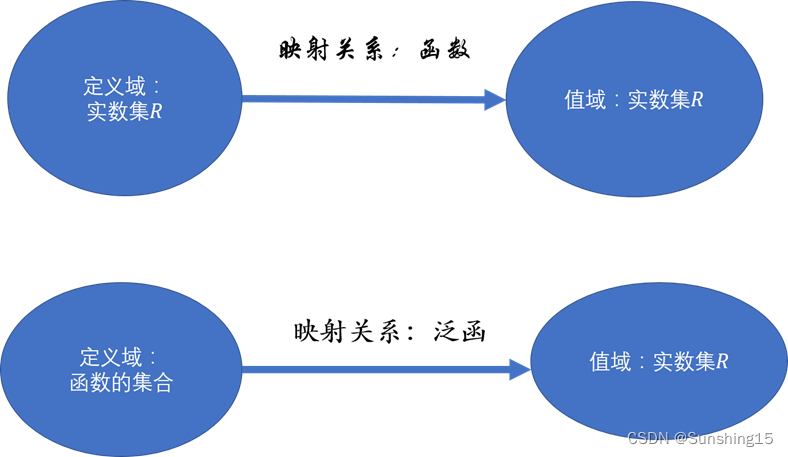
在这里插入图片描述

泛函即为以函数为自变量的一种映射到实数域的映射关系。而函数则是以某一实数为自变量映射到实数域的映射关系。这里的 $J [x (t)]$ 可理解为整条曲线 $x (t)$ 在映射关系 $J$ 下对应一个实数值。下面来解释一下泛函的自变量，如下图：
在这里插入图片描述
假设从[0,1]位置我们丢掷一个物体，该物体分别沿 $f (x)$ , $h (x)$ , $g (x)$ 三条轨道下落，同样都可降落至 [1,0]。那么我们可以将这个下落的过程称为一个泛函，三条下落的轨道曲线称为这个泛函的自变量，即泛函定义中的函数集合为 ${f(x),h(x),g(x)\}$ ，这个物体的高度位置即为映射关系 $J$ ，确定的数为高度0。

泛函的变分

自变量的变分

宗量：若函数 $x (t)$ 是映射关系 $J$ 的自变量函数，则称 $x (t)$ 为泛函 $J [x (t)]$ 的宗量函数。
宗量的变分：宗量的变分是指在同一函数类中的两个宗量函数间的差，即： $\delta x(t)=x(t)-x^*(t).$

泛函相近

零阶相近
当宗量的变分 $\delta x(t)$ 的绝对值对于 $x (t)$ 定义域中的一切 $t$ 都很小时，称函数 $x (t)$ 与 $x^*(t)$ 是接近的，也称为零阶相近。
一阶相近
当宗量的变分 $\delta x(t)$ 的绝对值以及 $\delta x(t)$ 的一阶导数的绝对值对于 $x (t)$ 定义域中的一切 $t$ 都很小，则称函数 $x (t)$ 与 $x^*(t)$ 是一阶相近的。
K阶相近
当 $x(t)-x^*(t)|$ , $|\dot{x}(t)-\dot{x}^*(t)|$ , $\ldots$ , $x^{(k)}(t)-x^{*(k)}(t)|$ 对一切 $t$ 都很小时，称函数 $x (t)$ 与 $x^*(t)$ 是 $k$ 阶相近的。

泛函距离

零阶距离
在连续函数全体组成的函数空间 $C [a, b]$ 中，泛函自变量的距离可定义为 $d[x(t),x^*(t)]=\displaystyle \max_{a\leq t\leq b}\{x(t)-x^*(t)\}$
$k$ 阶距离
由在区间 $[a, b]$ 上连续且具有连续的 $k$ 阶导数的函数的全体构成的函数空间 $C^{k}[a,b]$ 中，任意两个函数间的 $k$ 阶距离定义为 $d[x(t),x^*(t)]=\displaystyle \max_{a\leq t\leq b}\{|x(t)-x^*(t)|,|\dot{x}(t)-\dot{x}^*(t)|,\ldots,|x^{(k)}(t)-x^{*(k)}(t)|\}$

泛函的连续性

对于任意给定的正数 $\varepsilon$ , 总可以找到一个正数 $\delta$ , 使得当 $x^*)<\delta$ 时，有 $|J[x(t)]-J[x^*(t)]|<\varepsilon$ 则称泛函 $J [x (t)]$ 在 $x^*(t)$ 处是连续的。其中， $x^*)=\displaystyle \max_{a\leq t \leq b}|x(t)-x^*(t)|$ 。根据所采用的泛函自变量之间的距离的定义方式的不同，可分别定义泛函的零阶连续以及 $k$ 阶连续泛函。
Lemma 1: 如果函数 $F (t)$ 在区间 $t_0, t_f]$ 上是连续的，而且对于只满足某些一般条件的任意选定的函数 $\eta(t)$ 有 $\displaystyle\int_{t_0}^{t_f}F(t)\eta(t)dt=0$ , 则在区间 $t_0, t_f]$ 上有 $F (t) = 0$ 。

线性泛函

连续泛函 $J [x (t)]$ 如果满足如下两个条件： $J[x_1(t)+x_2(t)]=J[x_1(t)]+J[x_2(t)]$ $J [C x (t)] = C J [x (t)]$ 其中 $C$ 为常数，则 $J [x (t)]$ 为线性泛函。

泛函的变分

泛函的增量
由自变量函数 $x (t)$ 的变分 $\delta x(t)$ 引起泛函 $J [x (t)]$ 的增量 $\Delta J=J[x^*(t)+\delta x(t)]-J[x^*(t)]$ 为泛函 $J [x (t)]$ 的增量。
泛函的变分
当宗量函数 $x (t)$ 有变分时，泛函 $J [x (t)]$ 的增量 $\Delta J[x(t)]$ 可表示为 $\Delta J=J[x^*(t)+\delta x(t)]-J[x(t)]=\frac{dJ}{dx}|_{x^*}\delta x+\frac{1}{2}\frac{d^2J}{dx^2}|_{x^*}(\delta x)^2+R,$ 其中 $\Delta J$ 的线性部分称为泛函的变分，记作 $\delta J$ ，即 $\delta J=\frac{dJ}{dx}|_{x^*}\delta x，$ 换句话说即为泛函的变分是泛函增量的线性主部。

Lemma 2: 泛函的变分 $\delta J=\frac{\partial}{\partial \alpha}J[x(t)+\alpha \delta x(t)]|_{\alpha=0}$

Example 1: 计算泛函 $J=\displaystyle \int_0^1x^2(t)dt$ 的变分。
$\begin{aligned} \delta J&=\frac{\partial}{\partial \alpha}J[x(t)+\alpha\delta x(t)]|_{\alpha=0}\\ &=\frac{\partial}{\partial \alpha}\displaystyle\int_0^1[x(t)+\alpha\delta x(t)]^2dt|_{\alpha=0}\\ &=\displaystyle\int_0^12[x(t)+\alpha \delta x(t)]\delta x(t)dt|_{\alpha=0}\\ &=\displaystyle\int_0^12x(t)\delta x(t)dt \end{aligned}$

泛函的极值

泛函极值的定义

如果泛函 $J [x (t)]$ 在 $x(t)=x^*(t)$ 的邻域内，其增量 $\Delta J=J[x(t)-x^*(t)]=J[x(t)]-J[x^*(t)]\geq 0$ 或 $\Delta J=J[x(t)-x^*(t)]=J[x(t)]-J[x^*(t)]\leq 0$ 则称泛函 $J [x (t)]$ 在 $x(t)=x^*(t)$ 有极小值或极大值。

泛函的极值

强极值：如果 $J[x^*(t)]$ 是在与 $x (t)$ 仅仅具有零阶接近度的曲线 $x (t)$ 的泛函中比较得出的极值，称为强极值。
弱极值：如果 $J[x^*(t)]$ 是在与 $x (t)$ 具有一阶或一阶以上接近度的曲线 $x (t)$ 的泛函中比较得出的极值，称为弱极值。

泛函极值条件

必要条件
若可微泛函 $J [x (t)]$ 在曲线 $x(t)=x^*(t)$ 达到极值，则泛函 $J [x (t)]$ 在 $x(t)=x^*(t)$ 上的变分等于零，即 $\delta J[x^*(t)]=0$ 。
证明：对于任意给定的 $\delta x(t)$ 来说， $J[x^*(t)+\alpha \delta x(t)]$ 是实变量 $\alpha$ 的函数。泛函 $J [x (t)]$ 在 $x^*(t)$ 达到极值，即函数 $J[x^*(t)+\alpha \delta x(t)]$ 在 $\alpha=0$ 时达到极值，所以它的导数在 $\alpha=0$ 时应为零，即 $\frac{\partial}{\partial\alpha}J[x^*(t)+\alpha\delta x(t)]|_{\alpha=0}=0$ 由变分引理可知 $\frac{\partial}{\partial\alpha}J[x^*(t)+\alpha\delta x(t)]|_{\alpha=0}=\delta J[x^*(t)]=0$ 。得证。
充要条件
设可微泛函 $J (x)$ 存在二次变分，则在 $x=x^*$ 处达到极小值的充要条件为： $\delta J(x^*)=0,\delta^2J(x^*)>0.$ 同理，设可微泛函 $J (x)$ 存在二次变分，则在 $x=x^*$ 处存在极大值的充要条件为： $\delta J(x^*)=0,\delta^2J(x^*)<0.$