P13~16 第四章 电路定理——巧妙-灵性-智慧

1、叠加定理

-


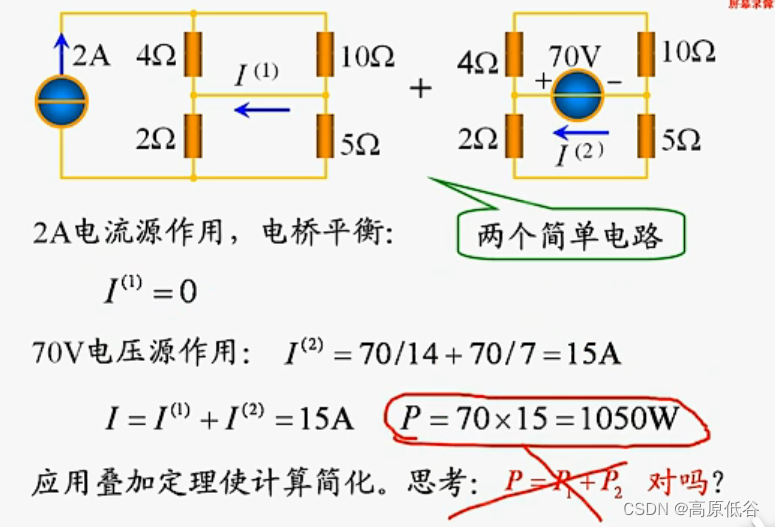
功率不能用叠加定理

拆解的太碎，电路碎片过多，此时每个碎片小容易求，但是要求的碎片数量比较多。碎片大点，每个碎片求解难度增加，但是要求的碎片数量减少。
下边是一种巧妙的情况，形成了两个单回路。

受控源与电阻地位相同，不参与单独的响应，而是控制量分量。因为很多时候控制量会因为独立电源置零，而发生变化。

2、齐性原理

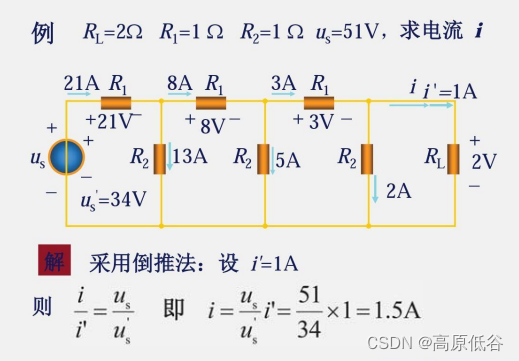
1、替代定理

图示表示：

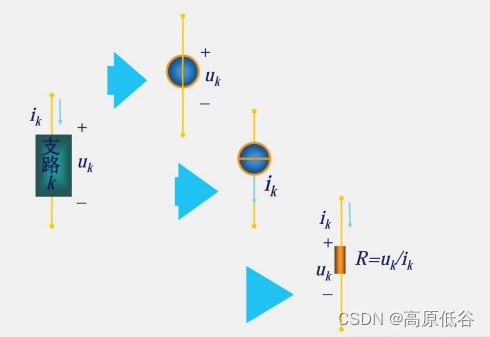
叠加定理和齐性定理只能用于线性电路，但是替代定理无论线不线性都可以用。
常见的：线性电路将某复杂支路等效成电压源或电流源之后，就可以使用叠加原理了。

引入两个相互抵消的电压源，拿其中一个去抵消支路电压。
对偶的思想：引入两个相互抵消的电流源，拿其中一个去抵消支路流。



回路当中只有电压源，就会导致电流不确定。
对偶：对结点连的都是电流源，那么该节点的电压就无法确定了。

2、替代定理的应用

配合和电流源串联的电压源可以去掉

实际电路设计，先根据功能模块设计电路，再用电路定理化简重构电路

电桥不平衡

3、戴维宁定理和诺顿定理

对于线性含由独立源的电路，可以等效的最简的结构，可以是电阻+电压源，两者是串联。也可以是电阻+电流源，两者并联。

4、用戴维宁定理和诺顿定理等效含源电路的前的思考（线性含源）

1）两种等效形式是等效的。

2）公式法——u=f(i)或i=f(u)

根据方程公式猜实际电路的等效结构

1、戴维南定理

2、戴维南定理的证明

对于线性含源的一个结构，

右边接一个支路N，再用电流源替代N

情况一：A没有独立源，那么A可以等价于一个电阻
情况二：A有独立源，例证法：
使用叠加法，进行非彻底拆分，
假设A中的独立电源由两个分别是m,n，
就可以先把电流源i去掉成开路，计算a,b间电压，得到电压分量u1,u1在此解不出。
再把独立源m,n去掉，计算a,b间电压，得到电压分量u2，同时可以知道去掉独立电源的N的等效电阻为Req。

最终由公式法得到：

3、定理的应用

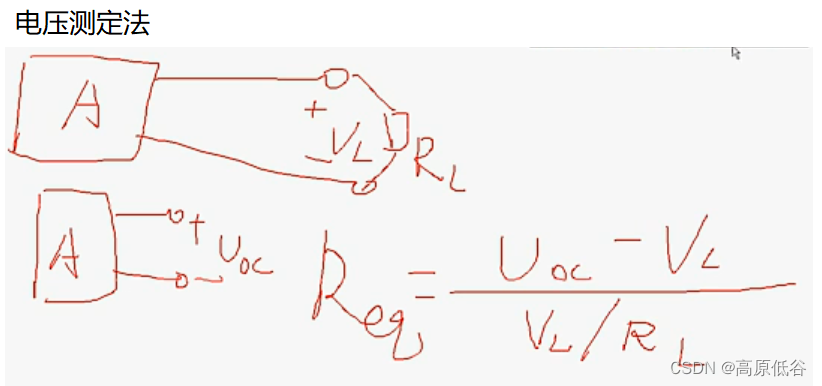
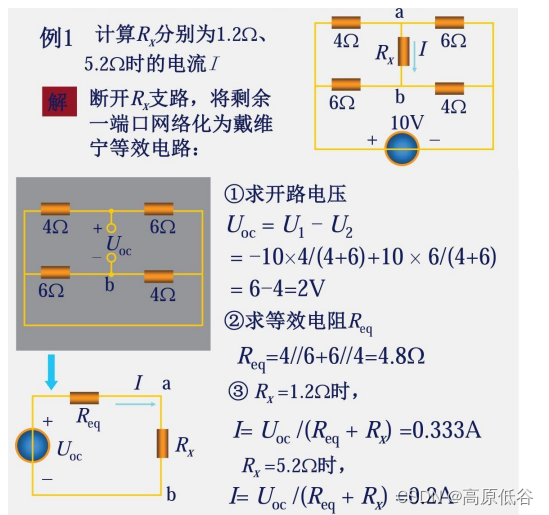
4、例题

对戴维南定理的认识：把电路当中拿出来，把剩余的东西进行戴维南化简。

1、诺顿定理的证明

诺顿定理的证明，
回忆戴维南定理的证明是，在a,b两端加上一个电流源，再根据叠加定理，就解电压Uab。
对偶原理：
在a,b两端加上一个电压源u，再根据叠加定理求A中的独立源作用是给到a，b的电流Iab’，再求在a,b两端加上一个电压源u作用时的电流Iab"，就解电流Iab=Iab’+Iab"。
Iab=Iab’+Iab"等价于公式法：Iab=Iab’-Geq*u(Geq是电导)

2、含源线性电路四种求解等效电阻（输入电阻）的方法

1）A中没有受控源，只有非受控源和电阻，串并联，串并混联，Y型，三角型求解
2）A中有受控源，和非受控源，电阻，可以用外加电源法，即假设外加电压，假设外加电流，即不加具体大小的电源，加一个大小位置的电源，当然也可以实际加明确大小的电源；可以假设ab间的电流（注意是从正极a流入A的电流），电压Uab，通过将电流源变成导线，电压源看出开路，再求比值得到的电阻就是输入电阻。
3）开短路法：

4）实验法：
加一个已知的电阻RL,体会对偶关系。

3、诺顿定理的使用——求短路电流输入电阻

分流公式：两个电阻R1、R2串联于电压为V的电路中,则：电流I=V/(R1+R2)

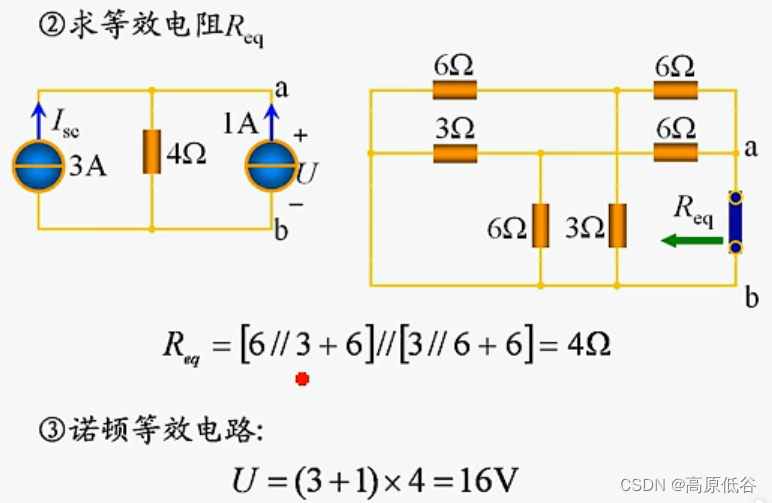
即等效电阻无穷大，就是开路，为零就是短路。

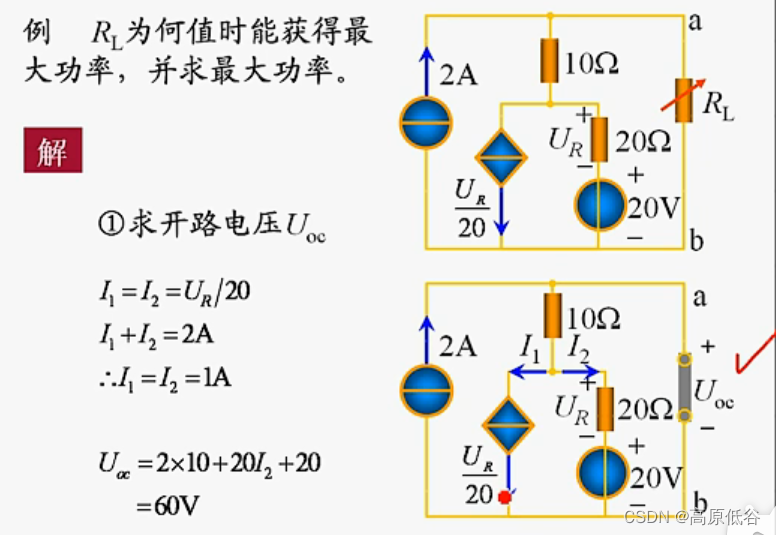
4、最大功率传输定理

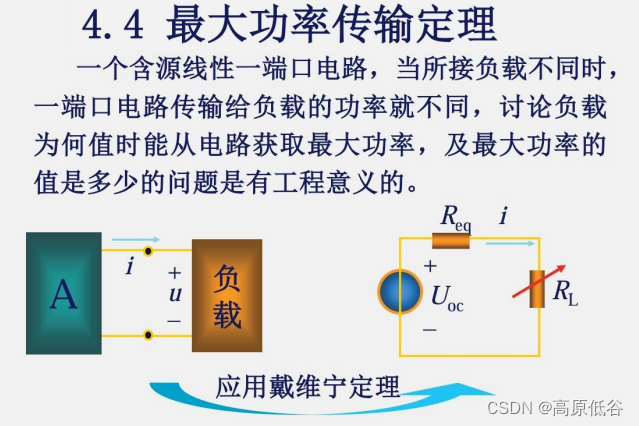
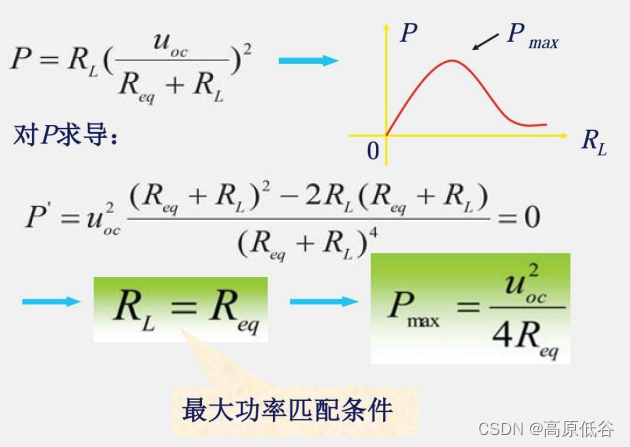
独立源置零


输入电阻不是电源内阻，效率是内阻上浪费的能量越多效率越低。
端口A的功率=输入电阻上消耗的功率+独立源上消耗的功率