欧几里得变换（Euclidean transformation）详解

生信小兔

已于 2022-07-05 09:08:46 修改

阅读量6.8k

点赞数 9

分类专栏：数学基础文章标签： python 几何学

于 2022-07-05 09:00:37 首次发布

本文链接：https://blog.csdn.net/weixin_60737527/article/details/125594852

版权

数学基础专栏收录该内容

14 篇文章 37 订阅

订阅专栏

欧几里得变换也称为欧式变换、刚性变换，是一种较为基本的变换，通过欧几里得变换，可以改变物体的空间位置，却不改变物体的形状、大小。欧几里得变换包括旋转变换（Rotation transformation）与平移变换(Translation transformation)。至于反射变换（Reflection transformation）,是比较有争议的，因为它是通过镜面对称(或平面中的轴对称)或点中心对称变换物体，所以有时认为它不属于欧氏变换，但是有时也认为是欧式变换。在本篇文章，兔兔为了将知识点讲述全面，将反射变换归到欧式变换中，并详细讲述旋转、平移与反射变换。

在关于欧式变换的文章中，有些着重讲述欧式变换群——这部分知识属于近世代数的群论部分知识，很少提到具体的操作过程，更多的侧重于抽象的理论。而在本篇文章中，着重讲述变换操作过程与算法实现，推导过程稍作介绍，不作重点，变换群的相关内容放到其它文章中讲解（这一部分与量子力学、量子化学或结构化学等内容相关）。

在变换操作中，一般分为对坐标系的变换以及对坐标系中物体的变换，事实上这两种变换本质上是相同的，如在直角坐标系下物体向某个方向平移一段距离，等价于坐标系向相反方向平移相同距离；物体绕某个轴沿某一方向旋转θ角，等价于坐标轴沿该轴向相反方向旋转θ角。所以，在本篇文章中，兔兔着重讲述对坐标系中物体的变换。

背景知识

1：坐标系

关于欧式变换，本文对平移、旋转与反射三种变换分别讲解。每种变换都先从二维平面空间开始，并拓展到三维空间。在每个空间内主要讲解对点的变换操作，因为对线、面、体的变换，与对点的变换有很大的关联（线、面、体由点组成）。并且所有操作都是在平面直角坐标系或空间直角坐标系（右手坐标系）下进行，点的表示分别采用笛卡尔坐标与齐次坐标。

（1）笛卡尔坐标(Cartesian coordinate)

笛卡尔坐标系是我们接触最多的一种坐标系，例如平面直角坐标系、空间直角坐标系等常见的直角坐标系，也包括斜坐标系。在该坐标系下，点可以由一个二维或三维的列向量来表示，如平面中原点 $(0,0)^{T}$ ，空间中的某一点 $(a,b,c)^{T}$ 等。

（2）齐次坐标（Homogeneous coordinate)

齐次坐标是本文研究变换的一个重点，运用齐次坐标，可以很方便地完成对物体的变换。简单来讲，一个点的齐次坐标就是它的笛卡尔坐标后加上1，如平面中原点的齐次坐标为 $(0,0,1)^{T}$ ，空间中某一点的齐次坐标为 $(a,b,c,1)^{T}$ 。

利用齐次坐标具有诸多优点。例如，判断点是否在直线 $ax+by+c=0$ 上，只需要判断 $(a,b,c).(x,y,1)^{T}$ 是否为0即可，这时平面直线可以用向量 $(a,b,c)^{T}$ 来表示，空间平面可以用向量 $(a,b,c,d)^{T}$ 表示，点是否在直线或平面上，只需判断两个向量的内积是否为0即可。

从上面例子中，我们发现，一个直线或平面的方程是不唯一的，上面的直线方程可以写成 $kax+kby+kc=0 (k \neq 0)$ ，也就是说，点的齐次坐标是可以表示成 $(kx,ky,k)^{T}$ ,即该点有无数种表示方法，如果归一化处理，每个值都除以k，就变成了 $(x,y,1)^{T}$ ,也就是前面讲到的齐次坐标的表示方法。如果齐次坐标中最后一个数是0而不是1，该点即表示为无穷远点。

2：变换的表示方法。

在本篇文章中，对于笛卡尔坐标，变换操作即为变换向量/矩阵作用于一个点的笛卡尔坐标（向量），一般为矩阵与向量的相乘或向量之间的相加；对于齐次坐标，即为变换矩阵T作用于一个点的的齐次坐标，运算都是矩阵相乘。本文旋转矩阵用R表示，平移向量由t表示，反射矩阵由S表示，点由向量 $\mathbf{r}$ 表示，变换矩阵由T表示。对物体的变换由相应的算子表示，如对点 $\mathbf{r}$ 的旋转操作可以表示成 $\hat{R}\mathbf{r}$ ，变换操作表示成 $\hat{T}\textbf{r}$ 。

一：平移变换

（1）原理

平移变换也是最为简单的一种变换。以平面中点的平移为例：设平移向量 $\mathbf{t}=(a,b)^{T}$ ，一个点的原坐标为 $\textbf{r}=(x,y)^{T}$ ,则平移后的点 $\textbf{r}+\boldsymbol{t}$ 表示为点r延向量t方向平移t的模长距离后的点。对于三维空间的点也是如此。

如果采用齐次坐标 $(x,y,1)^{T}$ 表示r，那么平移变换就可以表示成：

$\hat{T}\mathbf{r}=T.\textbf{r}=\begin{pmatrix}I_{2\times 2}&\textbf{t}\\\textbf{o}^{T}&1 \end{} . \textbf{r}$

其中 $I_{2\times 2}$ 为单位阵，t为平移向量，o为全0且维数为2的列向量。对于空间平移变换，单位阵为3×3维，向量t与o也都是三维列向量，变换矩阵为4×4矩阵。

（2）算法实现

import numpy as np
def translation(t,r):
    '''三维空间平移操作，t：平移的方向与距离，r：初始点齐次坐标'''
    T=np.mat([[1,0,0,t[0,0]],
       [0,1,0,t[1,0]],
       [0,0,1,t[2,0]],
       [0,0,0,1]])
    r=np.dot(T,r)
    return r
r0=np.mat([0,0,0]).T #初始点
t=np.mat([1,2,3]).T #平移向量
r1=translation(t,r0) #平移后点的齐次坐标
print(r1)

最终结果的齐次坐标，如果去除最后一个1，即得到笛卡尔坐标。

二：旋转变换

（1）原理

旋转变换与平移变换相比更为复杂一些，它需要确定旋转轴与旋转角度θ，我们通常认为绕轴逆时针旋转θ为正，逆时针旋转为负。物体在二维平面中的旋转，旋转轴是不能在平面内或与平面斜交（此时旋转物体会脱离平面，就变成了三维空间绕轴旋转），而是垂直于该平面的，所以在平面中看，是物体绕着一个点的旋转。我们先以平面一点绕坐标原点顺时针转θ角（坐标绕原点逆时针转θ）为例，推导过程如下。

上面采用两种方法来推导，第一种是根据向量在各个坐标系下不变，第二种为几何法。对于第一种方法，p表示坐标点在原坐标系下的坐标，p'表示在旋转后坐标系下的坐标，i,j为原坐标系的基矢，i',j'为旋转后的坐标系的基矢，并且i‘,j'可以表示成i,j分别在i',j'上的投影。如果是逆时针旋转，把θ取相反符号即可。在实际应用中，我们都以物体逆时针旋转角度为正。

在这里，我们不难发现，旋转矩阵是正交矩阵，即 $R^{T}=R^{-1}$ 。对点的旋转操作，为旋转矩阵左乘该点向量，如果旋转坐标轴，为旋转矩阵右乘原坐标系的基矢(i.j)。对物体的旋转等价于对坐标轴沿相反方向的旋转。

若平面中点p绕任意点o(a,b)旋转，推导过程与上面类似，但是较为复杂。比较好的方法是：把点p先沿 $(-a,-b)^{T}$ 平移，再绕原点旋转，最后再沿 $(a,b)^{T}$ 平移，这个过程涉及三步操作，可以由平移、旋转、平移这三个变换矩阵T依次相乘，得到的变换矩阵即为点p绕o点旋转的变换矩阵。

平面中关于原点旋转的旋转矩阵

$R=\begin{pmatrix}cos\theta &-sin\theta \\sin\theta&cos\theta \end{}$

表示点p绕原点逆时针旋转θ角操作，若平面中的点r用笛卡尔坐标表示，则R.r表示旋转后得到的点的笛卡尔坐标。

平面中的点用齐次坐标表示，旋转变换可以表示成：

$\hat{T}\textbf{r}=T.\mathbf{r}=\begin{pmatrix}R_{2\times 2}&\textbf{o} \\\textbf{o} ^{T}&1\end{}.\textbf{r}$

其中的R即为前面的旋转矩阵，T为变换矩阵。

在三维空间直角坐标系中，物体绕x轴、y轴与z轴逆时针旋转θ角的旋转矩阵分别为：

$R_{x}(\theta x)=\begin{pmatrix} 1&0&0\\ 0&cos(\theta x)&-sin(\theta x) \\ 0&sin(\theta x)&cos(\theta x)\end{}$

$R_{y}(\theta y)=\begin{pmatrix}cos(\theta y) &0&sin(\theta y)\\0&1&0\\ -sin(\theta y)&0&cos(\theta y)\end{}$

$R_{z}(\theta z)=\begin{pmatrix}cos(\theta z)&-sin(\theta z)&0\\sin(\theta z)&cos(\theta z)&0\\0&0&1 \end{}$

如果是物体绕通过原点的任意轴旋转，可以看成分别绕x、y或z轴若干角度得到的。（相继绕两个轴转θ1、θ2角度，等价于绕垂直于这两个轴的轴旋转2θ1+2θ2角度）。这样计算起来比较麻烦，兔兔在下面给出物体绕通过原点的任意轴旋转的旋转矩阵公式。

$R_{v}(\theta)=\begin{pmatrix} cos(\theta)+(1-cos(\theta)) x^{2} &(1-cos(\theta))xy-sin(\theta)z&(1-cos(\theta))xz+sin(\theta)y \\ (1-cos(\theta))yx +sin(\theta)z&cos(\theta)+(1-cos(\theta))y^{2}&(1-cos(\theta))yz-sin(\theta)x\\(1-cos(\theta))zx-sin(\theta)y & (1-cos(\theta))zy+sin(\theta)x & cos(\theta)+(1-cos(\theta))z^{2}\end{}$

其中v为单位向量，表示轴的方向，θ为旋转角度。

（2）算法实现

兔兔以平面中一点绕原点旋转为例，为了方便，直接采用旋转矩阵乘以向量的方法来进行变换。

import numpy as np
from numpy import sin,cos,pi
import matplotlib.pyplot as plt
def rotation(theta,r):
    theta=theta*pi/180 #角度转弧度制
    R=np.mat([[cos(theta),-sin(theta)],
             [sin(theta),cos(theta)]])
    r=np.dot(R,r)
    return np.array(r).flatten()
a=[3,0] #初始点
plt.figure(figsize=(6,6))
for i in range(72):
    b=rotation(5,a) #每次旋转5°角
    a=b
    plt.xlim([-5,5])
    plt.ylim([-5,5])
    plt.scatter(a[0],a[1])
    plt.pause(0.1)

最终的运行结果如下所示。

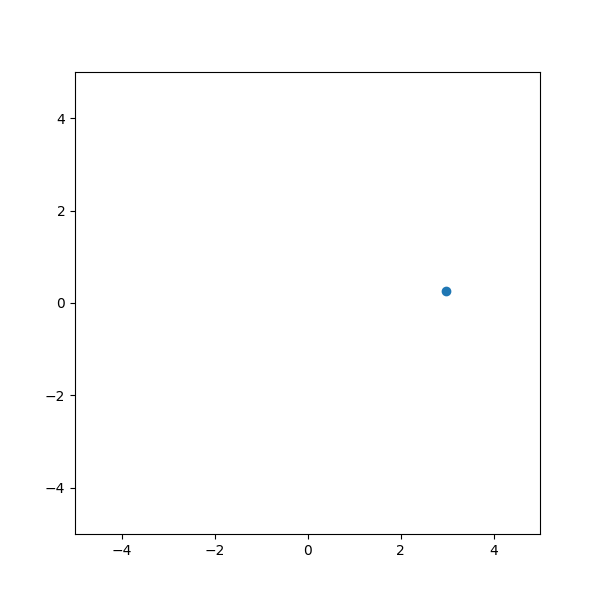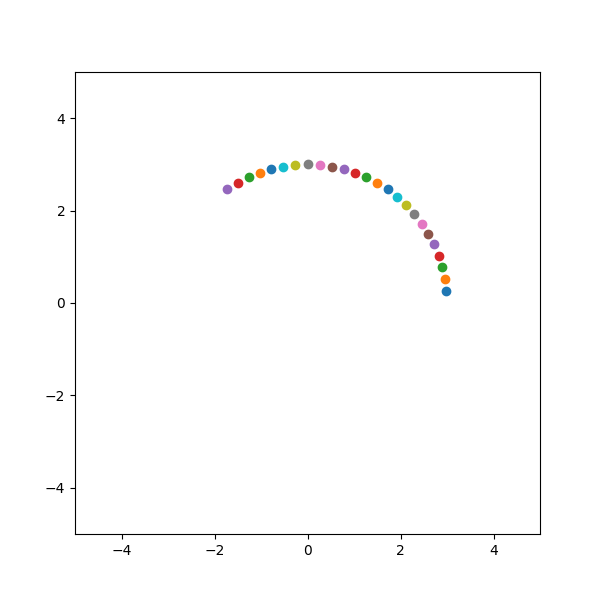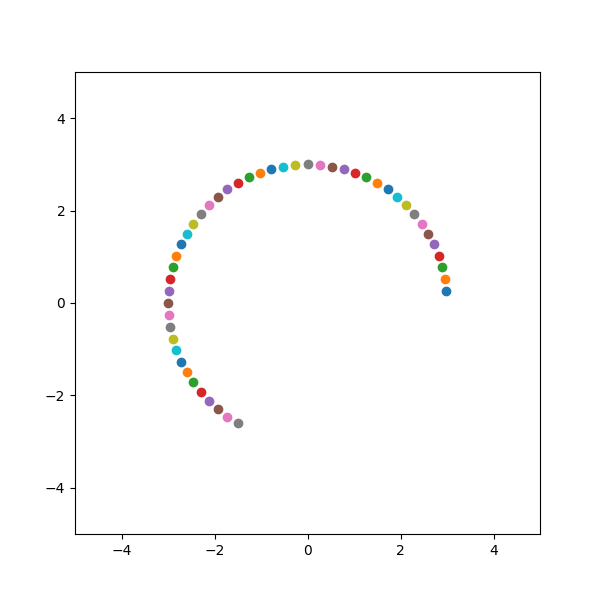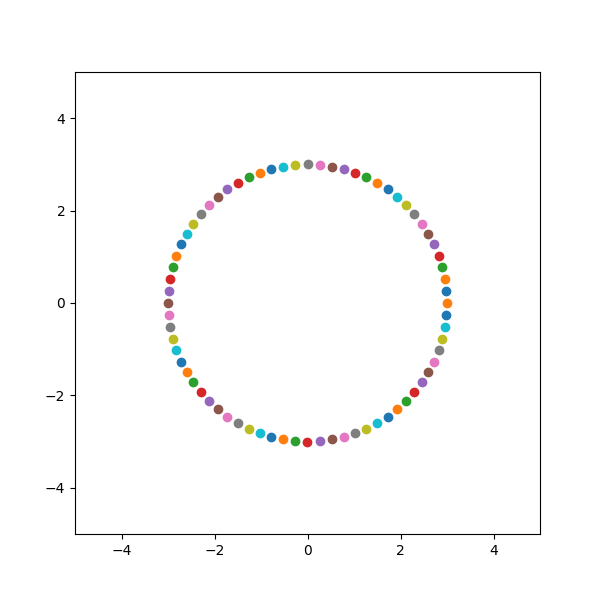
三：反射变换

反射变换与前两种变换有着本质的区别——对于一个物体，旋转与平移只是改变其空间位置，而反射变换可能会改变物体的手性，例如有机化学中的手性分子，通过反射变换后，前后两个物体就无法重合了。但是对于点，则不会出现这种情况。

反射变换实质上是一种对称操作，并且分为两类：镜面对称（即反映操作）与点中心对称（即反演操作）。关于镜面对称：在二维平面中，是物体关于某一条直线对称；在三维空间中，是物体关于某一平面对称，该变换即把物体关于某平面某直线或空间某平面对称，得到新的物体位置。关于点中心对称，即物体上所有点关于某一中心点对称。

（1）镜面对称（反映操作）

对于平面内的点p，笛卡尔坐标表示为(a,b)，它关于x轴对称得到的点为p'(a,-b)，那么此时可以表示成：

$p'=\begin{pmatrix}1&0\\0&-1 \end{}.p=S(l).p$

对于平面中的任意对称轴a'x+b'y+c=0，关于该轴对称操作的反射矩阵为：

$S(l)=\begin{pmatrix}1-2a^{2}&-2ab&-2ac\\-2ab&1-2b^{2}&-2bc\\0&0&1 \end{}$

其中a,b,c分别为： $\frac{a'}{n},\frac{b'}{n},\frac{c'}{n}$ ， $n=\sqrt{a'^2+b'^2}$ 。

同理，对于空间中的平面a‘x+b’y+c‘z+d’=0，关于该平面对称操作的反射矩阵为：

$S(\sigma)= \begin {pmatrix}1-2a^{2}&-2ab&-2ac&-2ad \\-2ab&1-2b^{2}&-2bc&-2bd\\-2ac&-2bc&1-2c^{2}&-2dc \\ 0&0&0& 1 \end{}$

其中a,b,c,d分别为： $\frac{a'}{n},\frac{b'}{n},\frac{c'}{n},\frac{d'}{n}$ ， $n=\sqrt{a'^{2}+b'^{2}+c'^{2}}$ 利用上述公式，只需要反射矩阵左乘某点的齐次坐标，就可以得到对称操作后的点的齐次坐标。

(2)点中心对称（反演操作）

点中心对称相对较为简单，利用初始点与对称点的中点在对称中心这一结论即可推导。

对于平面中的一点o(a,b)，关于该点中心对称的反射矩阵为：

$S(o)=\begin{pmatrix}-1&0&a\\0&-1&b\\0&0&1 \end{}$

对于空间中的一点o(a,b,c)，关于该点中心对称的反射矩阵为：

$S(o)=\begin{pmatrix}-1&0&0&2a\\0&-1&0&2b\\0&0&-1&2c\\0&0&0&1 \end{}$

利用上述公式，只需反射矩阵左乘某点的齐次坐标，就可以得到变换后的点的齐次坐标。

四：组合操作

对于变换操作 $\hat{T}$ ,旋转和平移的组合操作可以写成变换矩阵：

$T=\begin{pmatrix} R&\textbf{t}\\\textbf{o}^{T}&1 \end{}$

如果是二维空间内的变换，旋转矩阵R为2×2维，平移向量t，全0向量o为2维列向量，T为3×3矩阵；如果是三维空间内的变换，则R为3×3矩阵，平移向量t,全0向量o为3维列向量，T为4×4矩阵。而对于反射变换，是比较特殊的，虽然难以拆分成关于R，t , o,1分块矩阵的形式，但是其结构与前者还是有很多相同的地方。使用变换矩阵时物体坐标需要用齐次坐标。

旋转矩阵公式中给出的是绕通过原点任意轴的情况，如果绕不通过原点的轴旋转，只需先进行平移，平移方向为使得对称轴通过原点的移动方向，即原点到对称轴的垂线的垂足形成的的向量的反方向，再旋转θ角度，最后沿着该向量平移即可。求解平移向量，可以根据对称轴的方向向量(a,b,c)写出与该向量垂直且通过原点的平面σ方程：ax+by+cz=0，把对称轴直线方程用参数方程形式表示，联立求解得到垂足，进而得到平移向量。

对于空间中物体的连续操作，总变换矩阵即为各个变换矩阵的连续相乘，即T1.T2....。对于点的变换，只需要变换矩阵左乘该点的齐次坐标即可。

关于平面曲线、空间曲面的欧式变换，我们可以用参数方程来表示曲线或曲面方程，把参数方程写成齐次坐标形式，变换后得到的参数方程即为变换后的参数方程。

如果T是单位阵，可以看成旋转角为0（即不旋转），平移向量为0，也就是恒等操作，物体与原来位置相同。

五：总算法实现

在实际问题中，对三维空间物体的变换更为常见，所以兔兔在下面算法中以三维空间欧式变换为例。

import numpy as np
from numpy import sin,cos,pi
class Euclidean_transformation:
    def __init__(self,r):
        r.append(1)
        self.r=np.array(r) #初始点的齐次坐标
    def rotation(self,theta,v,p=True):
        '''旋转操作
        v:旋转轴方向矢量
        theta:逆时针旋转角度
        p:对称轴是否通过原点，默认通过原点,若不通过原点，p为对称轴所通过的某一点'''
        x,y,z=v
        n=np.sqrt(x**2+y**2+z**2)
        x,y,z=x/n,y/n,z/n #把方向向量转换成单位方向向量
        theta=theta*pi/180 #弧度制转成角度制
        R=np.mat([[cos(theta)+(1-cos(theta))*x**2,(1-cos(theta))*x*y-sin(theta)*z,(1-cos(theta))*x*z+sin(theta)*y,0],
                  [(1-cos(theta))*y*x+sin(theta)*z,cos(theta)+(1-cos(theta))*y**2,(1-cos(theta))*y*z-sin(theta)*x,0],
                  [(1-cos(theta))*z*x-sin(theta)*y,(1-cos(theta))*z*y+sin(theta)*x,cos(theta)+(1-cos(theta))*z**2,0],
                  [0,0,0,1]])
        if p==True:
            r = np.dot(R, self.r)
            return np.array(r).flatten()[0:3]
        else:
            a=-(x*p[0]+y*p[1]+z*p[2])/(np.sqrt(x**2+y**2+z**2))
            t=np.array([p[0]+x*a,p[1]+y*a,p[2]+z*a]) #原点到对称轴垂线垂足的向量
            self.translation(-t) #平移
            self.r=np.dot(R,np.mat(self.r).T) #旋转
            self.translation(t) #平移
    def translation(self,t):
        '''平移操作
        t:平移矩阵'''
        t=np.mat(t).T
        R=np.mat([[1,0,0,t[0,0]],
                  [0,1,0,t[1,0]],
                  [0,0,1,t[2,0]],
                  [0,0,0,1]])
        r=np.dot(R,self.r)
        self.r=np.array(r).flatten()
    def mirror(self,*sigma):
        '''反射变换中的镜像对称
        sigma:平面方程中系数a,b,c,d'''
        a,b,c,d=sigma
        n=np.sqrt(a**2+b**2+c**2)
        a,b,c,d=a/n,b/n,c/n,d/n
        R=np.mat([[1-2*a**2,-2*a*b,-2*a*c,-2*a*d],
                  [-2*a*b,1-2*b**2,-2*b*c,-2*b*d],
                  [-2*a*c,-2*b*c,1-2*c**2,-2*c*d],
                  [0,0,0,1]])
        r=np.dot(R,self.r)
        self.r=np.array(r).flatten()
    def central(self,*o):
        '''反射变换中的中心对称
        o:对称中心坐标'''
        a,b,c=o
        R=np.mat([[-1,0,0,2*a],
                 [0,-1,0,2*b],
                 [0,0,-1,2*c],
                 [0,0,0,1]])
        r=np.dot(R,self.r)
        self.r=np.array(r).flatten()
if __name__=='__main__':
    b=[0,0,0] #初始点坐标
    a=Euclidean_transformation(b)
    a.translation(t=[1,1,1]) #平移
    a.rotation(theta=180,v=[0,0,1],p=[0,1,0]) #旋转
    a.mirror(1,2,3,3) #镜像对称
    a.central(0,1,1)  #中心对称
    print(a.r)

总结

在本篇文章中，兔兔着重讲述了旋转、平移与反射三种变换，其中反射变换又分为镜像对称与中心对称。对于旋转矩阵和平移向量，两者既可以单独作用于点的笛卡尔坐标，也可以以变换矩阵T的形式左乘物体的齐次坐标，实现对物体的旋转和平移；而反射变换只能以变换矩阵T的形式左乘物体齐次坐标，实现变换。在实际应用中，我们更倾向于使用齐次坐标表示物体，使用变换矩阵实现对物体的连续变换，从而使操作更加方便。