相机与激光雷达联合标定（一）：坐标变换理论

一. 二维坐标系

1. 旋转矩阵

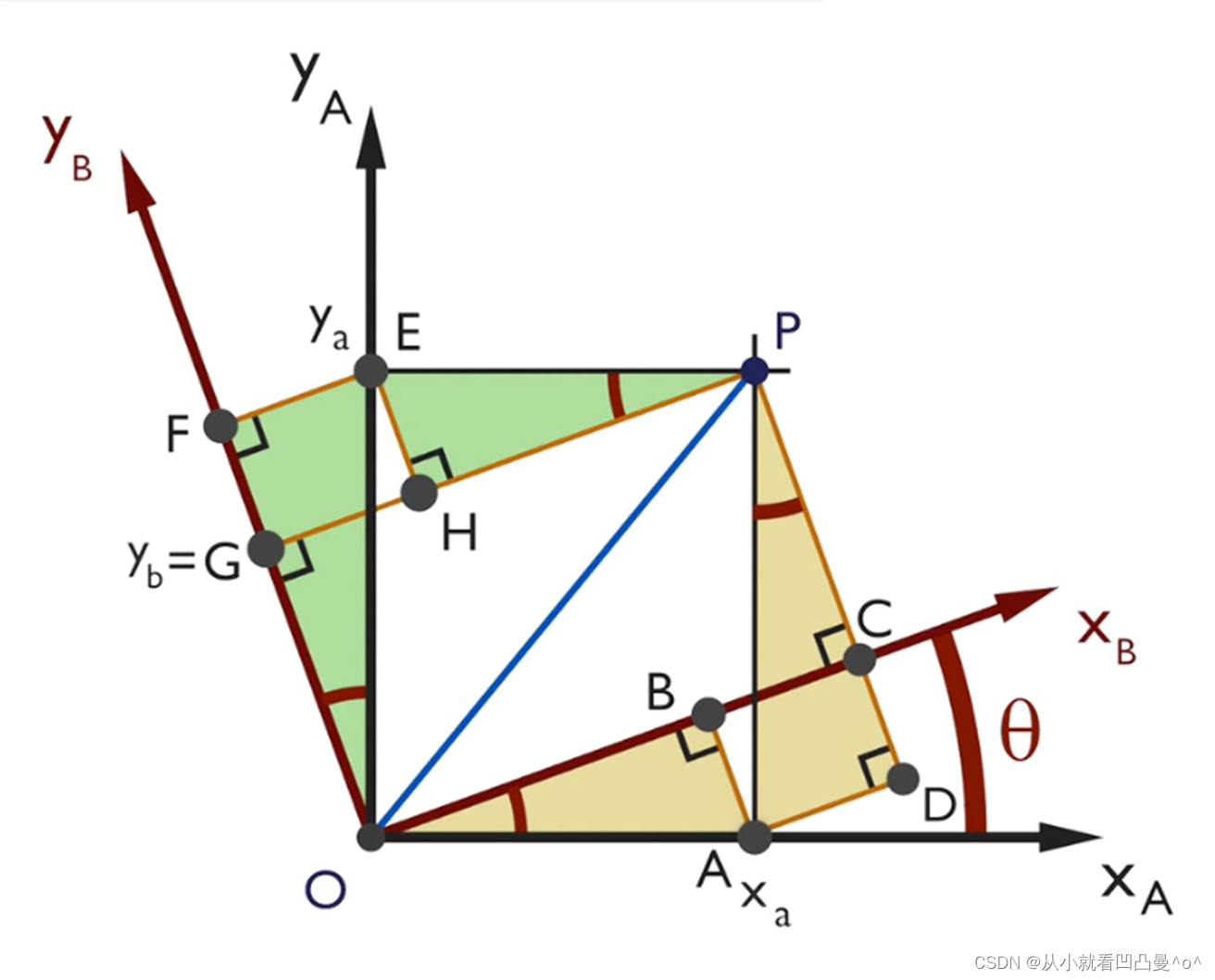
图1

在 图1 中，点P在坐标系下的位置坐标为(OA,OE)，在坐标系下的位置坐标为(OC,OG)

并且∠BOA=θ

OC=OB+BC   (式1)

OG=OF-FG   (式2)

在 式1 中：

OB=OA∙cosθ

BC=AD

AD=AP∙sinθ

AP=OE

AD=OE∙sinθ

                                                   ∴OC=OA∙cosθ + OE∙sinθ   (式3)

在 式2 中：

OF=OE∙cosθ

FG=EH

EH=EP∙sinθ

EP=OA

EH=OA∙sinθ

FG=OA∙sinθ

                                                   ∴OG=OE∙cosθ - OA∙sinθ   (式4)

联立 式3、式4 得：

   (式5)

因为：

所以 式5 将变成：

  (式6)

将 式6 转化为矩阵：

其中：

被称为旋转(Rotation)矩阵，记为R。

2. 平移矩阵

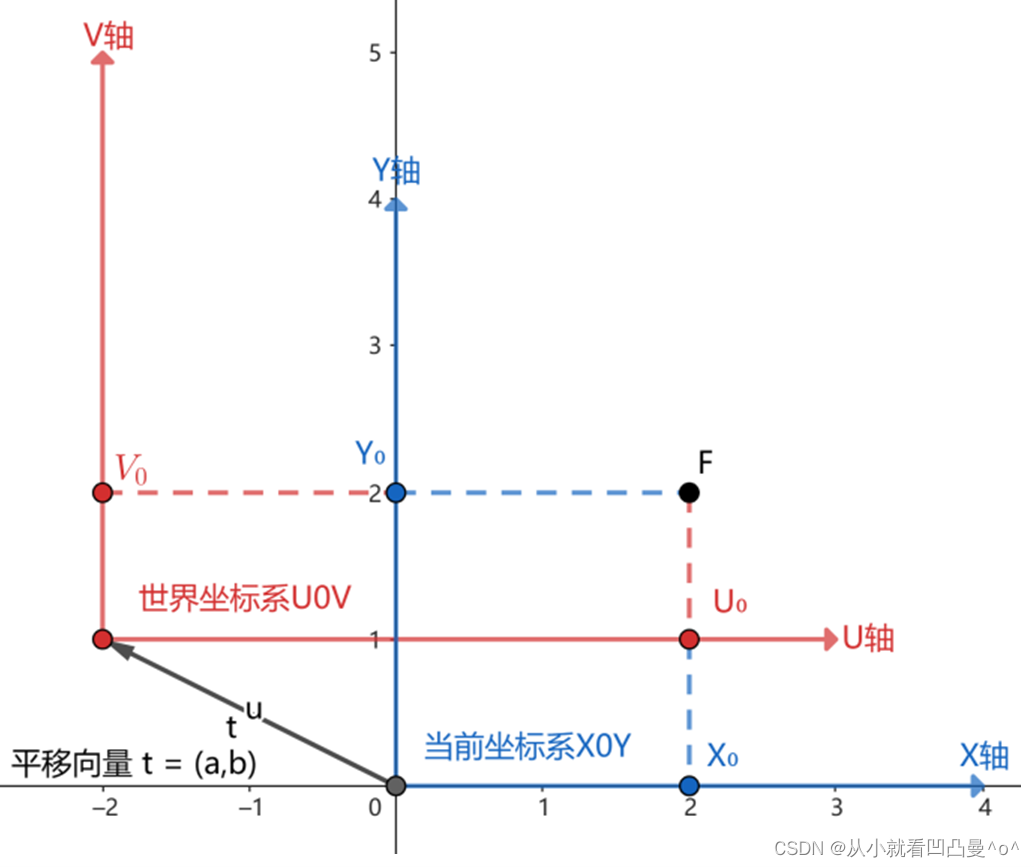
图2

假设 点F 在 图2 中XOY坐标系下的位置坐标假设是已知的 。将XOY坐标系沿着向量平移之后得到UOV坐标系，假设点F在图 2‑1中UOV坐标系下为

那么与的关系为：

   (式7)

将 式7 转化为矩阵：

其中：

被称为平移(Translation)矩阵，记为t。

3. 旋转平移矩阵

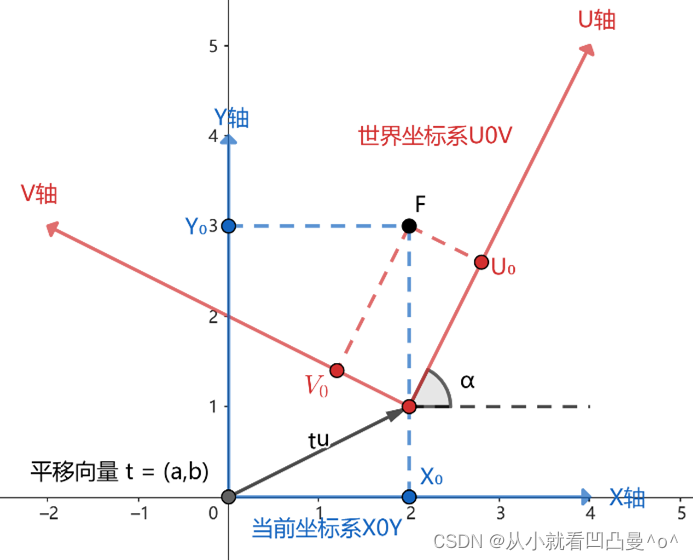
 图3

假设 点F 在 图2 中XOY坐标系下的位置坐标假设是已知的 。将XOY坐标系沿着向量平移并逆时针旋转α角度之后得到UOV坐标系，假设点F在图 2‑1中UOV坐标系下为 

上述变换过程可以理解为：

①. 先将XOY坐标系逆时针旋转α角度，得到坐标系，此时点F在坐标系下的坐标为

那么与 之间的关系为：

   (式8)

②. 再将坐标系沿着向量 移动，得到UOV坐标系，此时点F在UOV坐标系下的坐标为

那么与之间的关系为：

   (式9)

将 式8 带入 式9 中得：

   (式10)

将 式10 转化为矩阵：

   (式11)

其中：

为旋转(Rotation)矩阵，记为R。

为平移(Translation)矩阵，记为t。

则 式12 可以将写为：

其中：

被称为变换(Transformation)矩阵，记为T。

二. 三维坐标系

1. 旋转矩阵

三维坐标系的旋转可以借助二维坐标系旋转来理解，我们可以将三维坐标系的旋转分解为绕X、Y、Z轴的旋转。所以说，一个三维坐标系都可以由另一个三维坐标系通过绕X轴旋转、绕Y轴旋转、绕Z轴旋转、平移及其任何组合来实现。

(一). 绕Z轴旋转

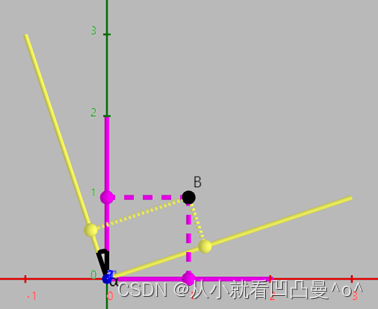
图4

假设空间中存在XYZ坐标系和UVW坐标系，两者满足以下条件：

• XYZ坐标系的原点和UVW坐标系的原点重合；
• 并且Z轴和W轴重合并指向相同方向。

（可以认为UVW坐标系是由XYZ坐标系绕Z轴（或W轴）逆时针旋转θ角度得到；也可以认为UVW坐标系是独立于XYZ坐标系单独存在的，并且Y轴与V轴夹角为θ度，X轴与U轴夹角为θ度。）

假设点B在 图4 中XYZ坐标系下的位置坐标为，在UVW坐标系下的位置坐标为

为方便理解，我们可以将视角沿着Z轴（或W轴）进行俯视观察，发现与二维坐标系旋转一模一样，所以：

与 的关系为：

   (式12)

将 式12 转化为矩阵：

(二). 绕X轴旋转

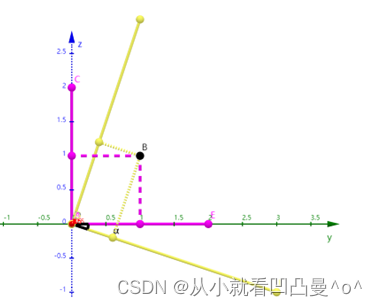
图5

假设空间中存在XYZ坐标系和UVW坐标系，两者满足以下条件：

• XYZ坐标系的原点和UVW坐标系的原点重合；
• 并且X轴和U轴重合并指向相同方向。

（可以认为UVW坐标系是由XYZ坐标系绕X轴（或U轴）逆时针旋转α角度得到；也可以认为UVW坐标系是独立于XYZ坐标系单独存在的，并且Z轴与W轴夹角为α度，Y轴与V轴夹角为α度。）

假设点B在 图5 中XYZ坐标系下的位置坐标假设为 ，在UVW坐标系下的位置坐标为

为方便理解，我们将视角沿着X轴（或U轴）进行俯视观察，我们发现：图4中的X轴变成了图5中的Y轴；图4中的Y轴变成了图5中的Z轴。所以我们将 式12 中的X0改成Y0、Y0改成Z0；将U0改成V0、V0改成W0。最后得出：

与 的关系为：

   (式13)

将 式13 转化为矩阵：

(三). 绕Y轴旋转

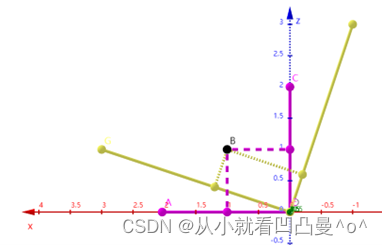
图6

假设空间中存在XYZ坐标系和UVW坐标系，两者满足以下条件：

• XYZ坐标系的原点和UVW坐标系的原点重合；
• 并且X轴和U轴重合并指向相同方向。

（可以认为UVW坐标系是由XYZ坐标系绕Y轴（或V轴）逆时针旋转β角度得到；也可以认为UVW坐标系是独立于XYZ坐标系单独存在的，并且X轴与U轴夹角为β度，Z轴与W轴夹角为β度。）

假设点B在图6中XYZ坐标系下的位置坐标为 ，在UVW坐标系下的位置坐标为

为方便理解，我们将视角沿着Y轴（或V轴）进行俯视观察，我们发现：图4中的X轴变成了图6中的Z轴；图4中的Y轴变成了图6中的X轴。所以我们将 式12 中的X0改成Z0、Y0改成X0；将U0改成W0、Y0改成U0。最后得出：

与的关系为：

   (式14)

将式14转化为矩阵：

(四). 总结

1.1. 绕X轴旋转时，某点在新坐标系下的位置 与原坐标系下的位置的对应关系：

1.2. 绕Y轴旋转时，某点在新坐标系下的位置 与原坐标系下的位置的对应关系：

1.3. 绕Z轴旋转时，某点在新坐标系下的位置 与原坐标系下的位置的对应关系：

2.1. 绕X轴旋转时，新坐标系与原坐标系之间的旋转矩阵 为：

2.2. 绕Y轴旋转时，新坐标系与原坐标系之间的旋转矩阵 为：

2.3. 绕Z轴旋转时，新坐标系与原坐标系之间的旋转矩阵为：

(五). 综合旋转

如果你想要一个坐标系UVW先绕着X轴旋转α，再绕着Y轴旋转β，最后绕着Z轴旋转θ角，这正情况被称为“左乘”（默认）

则得到的旋转矩阵R为：

令某一点在XYZ坐标系下的坐标为 ，在UVW坐标系下的坐标为，那么与的关系为：

U0V0W0=R∙X0Y0Z0

即：

    (式15)

2. 平移矩阵

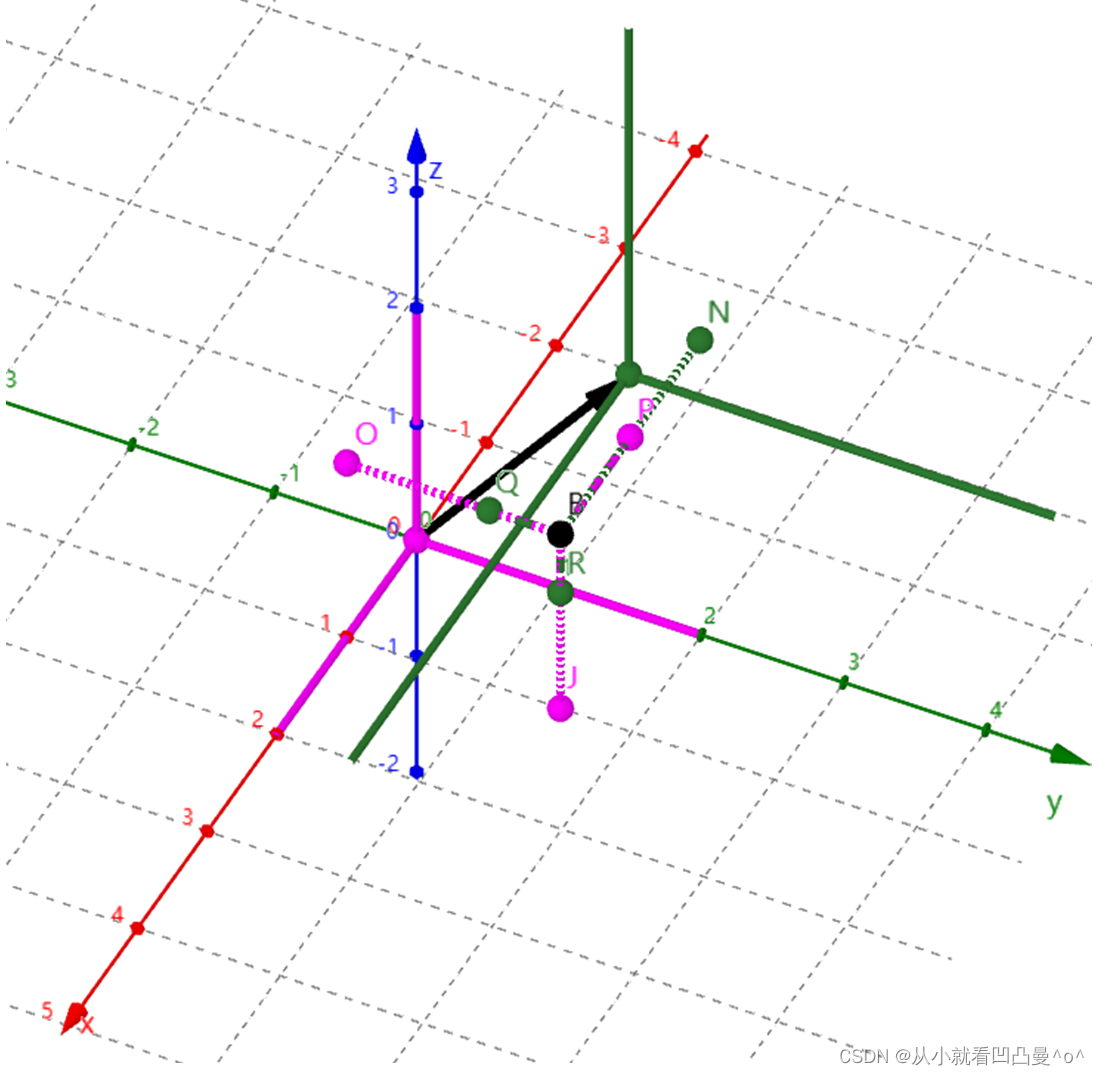
图7

假设在XOY坐标系下坐标为。

存在另一个坐标系UVW，（可以认为UVW坐标系是由XYZ坐标系沿向量平移得到的；也可以认为UVW坐标系是独立于XYZ坐标系单独存在的，并且X轴与U轴方向相同，Y轴与V轴方向相同，Z轴与W轴方向相同，UVW坐标系的原点在XYZ坐标系下的位置为 。）

点B在UVW坐标系下的坐标设为。

那么与的关系为：

   (式16)

将 式16 转化为矩阵：

其中：

被称为平移(Translation)矩阵，记为t。

3. 旋转平移矩阵

对于三维坐标系，我们可以将两个坐标系的变换过程视为先旋转、再平移的过程。

①先将一个坐标系先绕着X轴旋转α，再绕着Y轴旋转β，最后绕着轴旋转θ得到坐标系，那么令旋转矩阵R为：

②再将坐标系沿着向量方向移动，最终得到坐标系UVW

我们令某点在XYZ坐标系下的坐标为 ，在UVW坐标系下的坐标为 ，那么 与 之间的关系为：

其中：

被称为变换(Transformation)矩阵，记为T。