Receding Horizon “Next–Best–View” Planner for 3D Exploration论文笔记

最新推荐文章于 2024-10-27 15:33:53 发布

小旺蜀黍

最新推荐文章于 2024-10-27 15:33:53 发布

阅读量2.9k

点赞数 8

分类专栏：个人论文笔记文章标签： 3d 算法 ubuntu 后端

本文链接：https://blog.csdn.net/wyc648991806/article/details/122893742

版权

个人论文笔记专栏收录该内容

4 篇文章

订阅专栏

Receding Horizon “Next–Best–View” Planner for 3D Exploration

发表时间及出处： 2016 IEEE International Conference on Robotics and Automation (ICRA)

一、论文概述

二、系统概述

三、算法概述

3.1 后最佳视角（Next–Best–View）算法

3.2 信息增益（Information Gain）计算

3.3 实验结果分析

4. 算法优缺点

一、论文概述

本论文提出了一种不同于边界思想的探索方法，即后最佳视角（next-best-view）规划器，用于机器人未知环境探索，其目标点选取方法与frontier-base有所不同，所以是一种探索的新思路。该算法从作用范围来看，属于一种局部规划器，以机器人当前位置为根节点，使用RRT算法遍历空间，找到最佳目标点和最佳路径后，仅执行最佳路径的第一段，以此重复迭代，最终建立环境地图（octomap）。该算法的优缺点是：

优点：该算法注重局部规划，每次仅执行路径的第一段，有效减少了机器人回溯的次数，RRT随着探索的进行不断重置，规模小，有利于减少计算量。

缺点：该算法与frontier-base思想相比，以忽略全局信息为代价，减少计算量，可能会导致建图不完全的现象，不适合大场景、多通道的环境。此外，由于算法中使用了基于采样的RRT，无法解决此算法的通病，狭小入口不易进入。

二、系统概述

本文提出的系统结构与frontier-base大致相同，如下图所示。

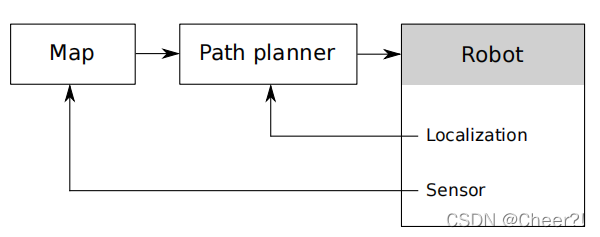
系统的核心是规划器（path planner），也就是本文主要的提出对象，它通过在地图上实现RRT寻找最佳节点，再通过执行第一条边导航之该点，同时实现找目标点和路径规划的功能，然后它的输出就是计算的路径，给到robot，通过移动自身的位置，然后通过sensor数据对地图进行更新，这就形成了一个闭环系统。

三、算法概述

3.1 后最佳视角（Next–Best–View）算法

其实大家从名称可以看出来，“next-best”意思就是只取下一个的意思。个人认为它与传统的frontier-base的思想有所不同的是，该算法在确定下一个最佳目标点后（此时已经规划好路径），只执行路径的前一小段，这个是一个创新点，等执行完这一小段之后，再次判断最佳点，这个做法可以避免规划器找到的最佳目标点不是全局最佳点（因为地图的信息是未知的！！），接下来详细说一下这个算法，伪代码如下：

该算法的一个迭代过程如下：

（1）将机器人当前的位置 $\small \xi _{0}$ 作为RRT生长的根节点，并设置好RRT的最大边数和最大节点数。

（2）RRT开始以当前位置为根进行生长（此处生长过程不再详述，请参考之前的博客），直到满足生长停止条件，RRT生长结束。结束条件如下：

（i）RRT上的节点数Nt已经达到最大节点数Nmax；

（ii）RRT上存在节点的信息增益（Information Gain） $\small g_{best}$ >0；

同时满足上述的两个条件，即可使RRT停止生长。

（3）找到 $\small g_{best}$ 最大的那个节点 $\small n_{best}$ ，并计算出由 $\small \xi _{0}$ 到 $\small n_{best}$ 的最佳路径 $\small \sigma_{best}$ （按照路径欧氏距离最短的原则，在RRT上找树枝相加即可）

（4）得到最佳路径后，删除树上所有的节点，然后（重点！！）仅执行这个最佳路径 $\small \sigma_{best}$ 的第一条边。如下图示意图。（PS：我画的时候保留了树的结构，实际算法里已经把树重置了）

上图中，绿色的线即为此次迭代过程实际执行的路径，说白了就是，找到了最佳点，但是不直接到最佳点，而是直到那个绿点就结束了，开始下一次迭代。

（5）反复迭代，直到满足探索结束的条件：

（i）RRT上所有节点的信息增益（Information Gain） $\small g_{best}$ =0；

（ii）RRT上的节点数Nt已经达到预定义的节点数Ntol；

同时满足上述两个条件，说明树已经长了很大了，已经遍及整张地图，但是信息增益为0，说明没有未知区域，那么探索结束。（其中，Ntol >> Nmax）。

3.2 信息增益（Information Gain）计算

本文的信息增益虽然是按照节点来的，但是增益是累加起来的，也就是说，当前节点的增益是由之前节点的增益累加得到的。公式如下：

上式中，Gain(nk)表示第Nk个节点的信息增益，Visible（…）表示机器人到了这个 $\small \xi _{k}$ 位置后所能观察到的未知单元的数量，即表示能探索出多大的未知区域，而后面的c（…）表示的σ这条路径的路径成本（即路径的长度），作为一个惩罚因子起作用，路径越长，信息增益越小。