概述
在上一次学习中,学习关于坐标系的那些事。这次学习继续往下,学习在坐标系中的点和矢量。了解点和矢量的区别,以及一些基本运算。
点
点的概念比较简单:点是n维空间中(游戏中指二维或者三维)的一个位置。
点没有大小,方向。它仅仅表示一个位置。
点的表示,通常使用一组数字来表示一个点P,二维和三维空间的点表示如下:
二维空间的点:
三维空间的点:
矢量
矢量 — 也被称为向量(vector)。
矢量的表示也是一组数字,这不是和点一样了么!!!!没错,虽然表示方法看上去是相似的,但是矢量的定义比起点来说要复杂了一些。
矢量指的是n维空间中一条包含了模(大小)和方向的有向线段。
与矢量对应的是:标量(只有大小没有方向)。
矢量和点的区别:
矢量是一个有向线段,包含了模和方向,它没有位置的概念,只要矢量的模和方向不变,无论放到哪里都是同一个矢量。点是一个位置,没有大小和方向。
矢量的运算
下面开始,来了解一下矢量的一些常见运算。这些运算都相对比较好理解。
1、矢量和标量的乘法/除法
矢量和标量可以进行乘除法运算。但是不能进行加减法。
这个运算很简单,直接给出公式。就是使用标量分别乘以矢量的各个分量:
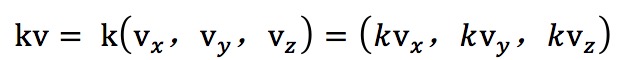
关于矢量和标量的乘除法,从几何意义上可以看做是对矢量V进行一个大小为|k|的缩放。若k<0,那么这个矢量的方向还会和原矢量相反。
2、矢量的加减法
上面我们提到了,矢量不能和标量进行加减法。但是矢量可以和矢量进行加减法运算。
ps:参加矢量加减法的两个矢量,维度必须相同。
矢量的加减法,就是将两个矢量的对应分量的进行加减法运算即可。
向量加减法的几何意义:
1、向量加法的几何意义:向量a、b相加,可以看成是将向量a的头平移连接到向量b的尾,然后将向量a的尾和向量b的头连接就构成一条新的向量。
这条新的向量就是a + b。如下图:
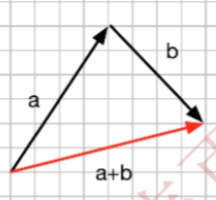
关于向量加法的运算的几何意义,就是一个三角形法则。
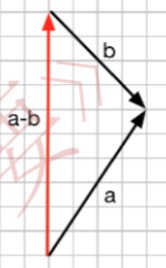
2、向量减法的几何意义:向量a、b相减,将向量b的尾平移到和向量a的尾的位置重合。然后将向量b的头和向量a的头连接就构成了一条新的向量。
这条新的向量就是a - b。如下图:
3、矢量的模
矢量是有大小和方向的。
矢量的大小就是它的模。矢量的模是一个标量,矢量的模可以理解成是矢量在空间中的长度。它用两条竖线包裹矢量表示。例如:|v|。
模的计算公式如下:
4、单位矢量
矢量是有大小和方向的。上面我们已经知道了如何计算矢量的大小(模)。现在来看下如何获取到矢量的方向。
在很多情况下,我们只关心矢量的方向而不是大小。例如:在计算光照模型的时候,我们往往需要得到法线和光源方向,这个时候我们就不用关心这些矢量有多长。
计算矢量的方向就是计算单位矢量。 单位矢量就是:模为1的矢量。单位矢量的计算过程被叫做归一化。
ps:零向量是没有单位矢量的。
单位矢量的计算就是使用矢量的各个分量除以这个矢量的模长。
单位矢量的计算公式:
ps:由上面的公式可以看出,为什么零向量不能被归一化。因为零向量的模长为0,分母为0没有意义。
5、矢量的乘法
之前我们说过,矢量可以和标量进行相乘。最后的结果是对原矢量的缩放并且可能会造成方向相反。那么矢量和矢量之间可以进行相乘么?答案是可以的。
矢量之间的乘法与矢量和标量之间的乘法有很大不同,分为两种:
- 点积 — 也叫作内积
- 叉积 — 也叫作外积
下面就来对他们分别进行介绍。
5.1、点积
点积的名称来源于它的运算符号。
对矢量a和矢量b进行点击操作。表示为:
ps:矢量之间的点号是不能够省略的。
点积的公式有两种形式:
公式一:
两个矢量的点积,就是将两个矢量的对应分量相乘后再取和。最后的到的结果是一个标量。公式如下:
点积的第一个几何意义 — 投影
假设,有一个单位矢量a和另外一个长度不限的矢量b。现在希望得到矢量b在矢量a上的投影。这时候就能够使用点积来得到投影结果。如下图: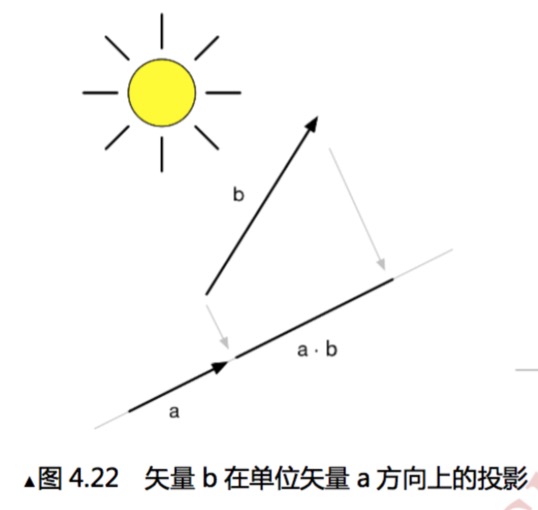
ps:投影的值可能是负数。投影值的符号与单位矢量a和矢量b的方向有关。当方向相反时(夹角大于90°),结果小于0。当方向相同时(夹角小于90°),结果大于0。当方向互相垂直时(夹角等于90°),结果等于0。疑问:如果这里的单位向量a不是单位向量也是任意长度的向量,那么结果会是什么样的?
答案是:结果是等于单位向量a和向量b的点积再乘以a的模长。
点积还有几个重要的性质:
1、点积可结合标量乘法:
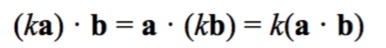
2、点积可结合矢量加法和减法:
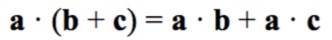
3、一个矢量和本身进行点积的结果是该矢量模的平方。
公式二:
公式二从三角代数的角度出发,这种形式可以更明确的强调出两个矢量之间的角度关系。公式如下:
疑问:这个公式到底是怎么来的?
还记得上面我们说到的向量b投影到向量a上就是它们的点积吗?看下图:
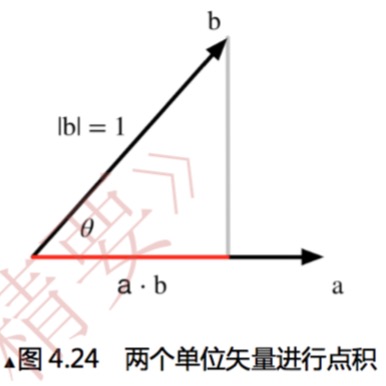
可以看到,用向量a和向量b可以构建出一个夹角。点积的结果刚好是这个夹角的邻边。假设现在矢量b是单位矢量。
根据: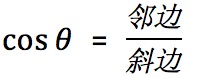
可以知道: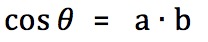
由性质1进行扩展一下,假设这时候向量a和向量b都不是单位矢量了那么就能够得到最后的公式:
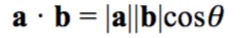
从这个可以更清楚的看出点积的结果和夹角之间的关系。这也就是投影的时候为什么会有不同符号投影值的原因。
5.2、叉积
矢量的另一种乘法运算是叉积。与点积不同的是,点积的结果是一个标量。而叉积的结果还是一个向量。
叉积的运算符号同样来自于它的运算符号。表示为: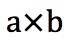
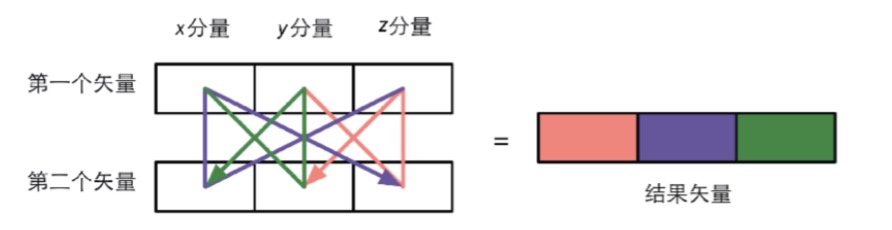
叉积的公式相比于点积来说复杂一些:
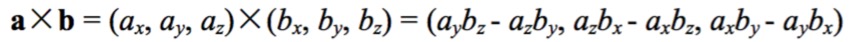
其实这个公式是有规律的,如下图:
ps:叉积既不满足交换律也不满足结合律。
但是叉积满足反交换律
叉积的几何意义:
对两个矢量进行叉积的结果是一个垂直于这两个矢量的新矢量。那么这个新矢量的模和方向应该怎么计算呢? 叉积的模长公式如下:
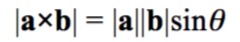
可以看到这个公式和点积的公式二非常相似。不同的是这里使用了正弦值。
作者的书中说到:这个公式和平行四边形的公式是一样的。反正我是忘记了O(∩_∩)O哈哈哈~。
那么来构建一个平行四边形。如下图:
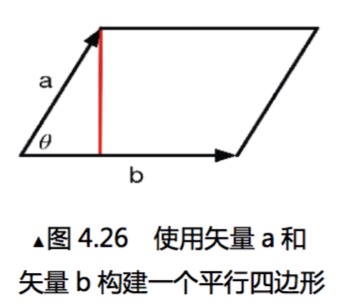
这里的高h使用矢量a的模长和夹角的正弦值来求得。最后再用这个求得的h乘以矢量b的模长就能求得到叉积的模长。
ps:若矢量a和矢量b的反向相同或者相反,那么构建出来的新矢量就是一个零矢量!!!








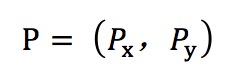
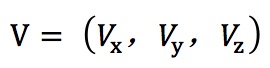
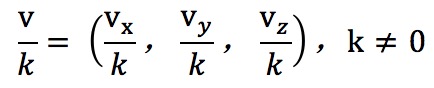
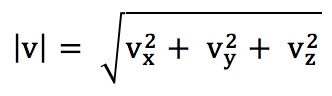

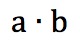
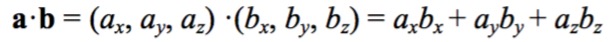
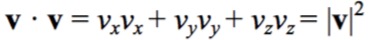
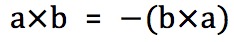














 1064
1064

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








