前言
我又消失了一段时间,这段时间研究了惯性导航有关的算法,整理了不少博客,字数比较多,图片比较多。学到了很多知识。
2023/8/5补充,惯性导航的滤波算法比较复杂,分析起来很难以理解
IMU滤波要考虑两种实际应用场所,一是分析惯导的姿态,二是分析位置(包含速度),为什么要将这两个区别开,主要是因为粗对准后就可以进行简单的姿态分析,推算位置算则需要进行精对准
分析位姿主要是使用姿态解算方法
卡尔曼滤波与互补滤波(比方说Mahony)是在惯性导航中常用的两种滤波方法,它们都用于融合陀螺仪和加速度计等传感器数据以得到更准确的姿态和位置估计。
卡尔曼滤波是一种优化的滤波方法,通过最小化估计值与实际测量值之间的误差来得到最优的状态估计。它考虑了系统的动态模型和传感器的测量误差,能够减小传感器噪声和漂移的影响,提供较为精确的估计结果。
而互补滤波是一种简单而直观的滤波方法,通过将陀螺仪和加速度计数据进行加权平均来融合,其中加速度计主要用于姿态的长期稳定性,而陀螺仪主要用于短期的姿态响应。这种加权平均的方式能够在不引入过多复杂计算的情况下提供相对准确的估计结果。
卡尔曼滤波相对于互补滤波来说,理论上更为精确和优化,尤其在动态环境下有较好的表现(其实就是算法能够自动的调整权重)。然而,卡尔曼滤波在实现上更加复杂,需要较大的计算量和存储资源。相比之下,互补滤波简单易实现,适用于资源受限的嵌入式系统或实时应用。
因此,在实际应用中,选择使用卡尔曼滤波还是互补滤波取决于具体的应用场景、计算资源以及对姿态和位置估计的要求。在某些情况下,也可以将两种方法结合起来,以充分利用各自的优势,提供更稳定和准确的导航结果。
本节介绍
这一节主要介绍关于IMU相关算法的阅读与思索,准确的说是介绍(姿态)Mahony算法和卡尔曼滤波算法。一般使用的都是四元素,如果你现在后面的公式推导中看到了旋转矩阵还有欧拉角之类的,知道他们能够相互转化就行了。
0、AHRS姿态解算
明白:没有磁强计,仅仅通过六轴IMU的滤波算法,是不能算出精确的偏航角的(航向角),感觉更多的是因为单纯的航向角试图通过角速度积分或造成很大的误差
一、Mahony算法
在叙述mahony算法之前,先说一下最经典的PID控制算法。
1.1 PID控制算法
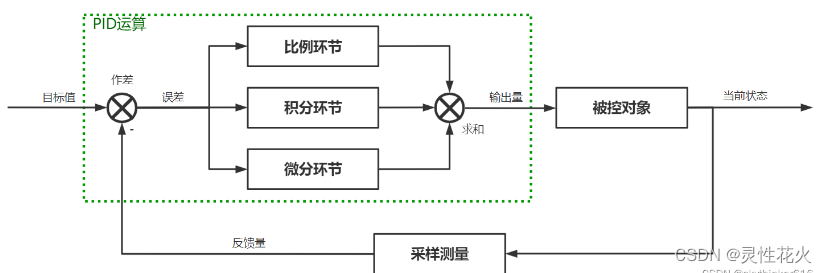
这个算法接触的很长了,但是一直没有考虑在STM32上是如何运转的。这位博客大佬PID具体原理说的很好,就不搬运了
(65条消息) PID超详细教程——PID原理+串级PID+C代码+在线仿真调参_skythinker616的博客-CSDN博客
不过还是要简单说一下PID的控制步骤:
比例P:提供反方向力产生加速度,迫使反向方向运动,但是往往这种力不会平衡,甚至有可能永远震动下去。
积分I: 主要是平衡干扰力的影响,达到预期的平衡点。
微分D:利用一阶积分实现达到预计平衡的作用,但是一般难以实现设计。
上面博主介绍的非常仔细,如果看完了可以直接考虑物理量的设计这一环节,也就是:
目标值、反馈值、输出值的考虑
我们的想法是让MPU输出有效的陀螺仪还有加速度计的数据,但是这个距离我们设计的步骤还有一些遥远。
比方说:虽然我们在上节的介绍通过IIC能够printf打印6050直接得到了6个数据,我们知道这些数据是不准的,但是在PID来滤波,怎么得到真实值?也就是说我们让这6组数据达到什么效果?PID的反馈值如何设定?
其实:PID控制的时候并不是直接控制这六个参数,而是根据这六个数据输出位姿,控制位姿。此外,目前市面上大多都是采用PID来控制小车,所以在回馈量上都是关于小车的量,纯惯导与这个没有多大的的关系,对于主流的小车PID差速控制之类的就不做过多的研究。
经过一段时间的调研和查询,发现实际做惯导的时候并不是仅仅使用PID控制的(或者说用PID控制的比较少),而是使用mahony算法,还有卡尔曼滤波算法。
1.2 模糊PID
2023/4/14补充模糊PID,在某私密算法中看到的
感谢博客(80条消息) 【智能车】模糊PID控制原理详解与代码实现_Ethan-Code的博客-CSDN博客
普通PID的参数Kp以及Ki都是要自己不断调节的。可以说换了一个环境就需要调一次。不过有一种PID的参数是可以自己变化,那就是模糊PID了(虽然他自己调过程的比一般PID要更多了)。一般这种方法用在四驱小车中,我同门和我说这种方法用在惯导设备中的效果其实并不是很好。谁知道呢?就像基于深度学习的PID(自己学Kp,Ki)。
扯远了,这里不做扩充,知道Mahony后面是使用PID其实可以换算成模糊PID实现自动调参就行。
1.3 Mahony算法
(65条消息) 电赛四轴小结——姿态解算篇【mahony互补滤波算法】_linzs.online的博客-CSDN博客
上面博客介绍的Mahony算法大意是这样的:
加速度计会给出三组数据,这三组数据在IMU模块(DMP可能会固件滤波一下)是直接使用的。但是考虑到误差,一般通过平衡时候的重力加速度[0 0 g]T通过计算求出位姿变化矩阵中的参数(但求不出航向角)。
陀螺仪的加入则是弥补了加速度计的这种不确定性。陀螺仪解决的是:角度变化与时间的比,单位:度/秒,如果说世界是理想的、只需要对3个轴的陀螺仪角速度进行积分,得到3个方向上的旋转角度,也就是姿态数据。
磁力计的加入主要是实现航向角的输出。不过做惯导一般不考虑航向角。
在理想世界,陀螺仪和加速度计都能实现输出位姿。实际上陀螺仪解算得到的姿态具有良好的高频特性,但是会随着时间漂移,而加速度计解算得到的姿态具有良好的低频特性,不会随着时间漂移,但是载体剧烈运动时,往往不能解算出真实的姿态。所以我们可以将陀螺仪的高频特性和加速度计的低频特性相融合,得到高频、低频特性都很好的算法。
这就是mahony算法的核心点——数据融合(互补滤波)
直白一点的说:融合加速度计还有陀螺仪数据进行位姿估计,也就是博客说的:
-加速度计告诉我们:“你现在的位置是Racc”
-我们回答:“谢谢,但让我确认一下”
-然后根据陀螺仪的数据和上一次的自己计算出来的准确值修正这个值并输出新的估算值。
接下来就是进一步的公式推导步骤了,建议参考贴吧:
Mahony姿态解算算法笔记(一) - 知乎 (zhihu.com)
Mahony姿态解算算法笔记(二) - 知乎 (zhihu.com)
该博客推导过程挺好理解的:
1.陀螺仪测出的角度转化为四元素,然后计算姿态矩阵
2.利用实际重力加速度只有一个分量,保持不动,会有轻微的误差,认为就是简单的姿态变化,通过上面获取的位姿将加速度转到目前的加速度(积分后就是速度),在与理论速度叉乘
3.根据(err=V1叉乘V2 -> err=|a1t||a2t|sinθ -> err =|1||1|sinθ -> err=θ )得到误差
1.4 加入磁力计
加入磁力计的目的是为了更加精准的计算航向(yaw),上面Mahony计算的航向角的方式会因为1/cos 导致接近二分之派误差会逐渐离谱(此外还会有误差累积),所用磁力计对准磁北进行求取航向角,其精度要好得多
参考博客
[知识点]基于加速度计与磁力计的姿态解算方法(加计补偿偏航) - 知乎 (zhihu.com)
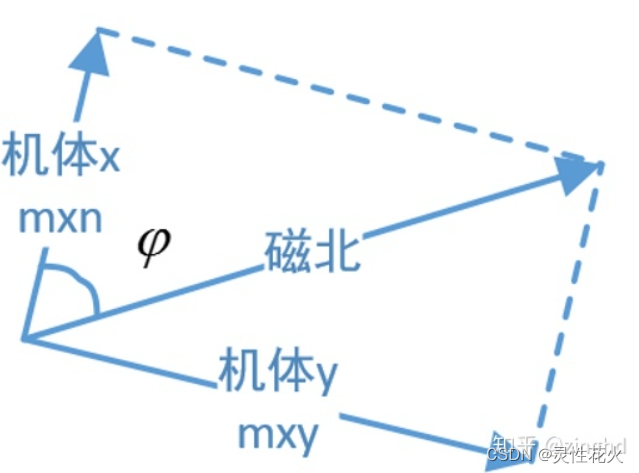
简单的说:磁北不一定与水平面完全重合,所以一般可以看成是一个斜向量(磁北),可以拆分成为与当地水平面平行(x)和与当地水平垂直的向量(y)。
所以我们保持磁力计水平的时候,三个量的方向就会与磁北的方向重合,所测出的数据就能够反应测量数值
考虑到变化情况,一般将器件指向北极,这样偏航角输出就是0。但是实际情况磁北是不能严格的绝对水平,所以我们假设有一定的变化角度(roll、pitch没有偏航角,因为固定住了)。即需要有旋转矩阵才能将b系读出的数据转到n系上也就是博客中谈到的
最后该算法还是用到了PID进行闭环控制。
代码参考Mahony姿态解算算法笔记(二) - 知乎 (zhihu.com)
代码还可以参考(初始参数不一样)AHRS互补滤波(Mahony)算法及开源代码_路痴导航员的博客-CSDN博客
// Definitions #define sampleFreq 512.0f // sample frequency in Hz #define twoKpDef (2.0f * 0.5f) // 2 * proportional gain #define twoKiDef (2.0f * 0.0f) // 2 * integral gain // Variable definitions volatile float twoKp = twoKpDef; // 2 * proportional gain (Kp) volatile float twoKi = twoKiDef; // 2 * integral gain (Ki) volatile float q0 = 1.0f, q1 = 0.0f, q2 = 0.0f, q3 = 0.0f; // quaternion of sensor frame relative to auxiliary frame volatile float integralFBx = 0.0f, integralFBy = 0.0f, integralFBz = 0.0f; // integral error terms scaled by Ki void MahonyAHRSupdate(float gx, float gy, float gz, float ax, float ay, float az, float mx, float my, float mz) { float recipNorm; float q0q0, q0q1, q0q2, q0q3, q1q1, q1q2, q1q3, q2q2, q2q3, q3q3; float hx, hy, hz, bx, bz; float halfvx, halfvy, halfvz, halfwx, halfwy, halfwz; float halfex, halfey, halfez; float qa, qb, qc; // Use IMU algorithm if magnetometer measurement invalid (avoids NaN in magnetometer normalisation) // 在磁力计数据无效时使用六轴融合算法 if((mx == 0.0f) && (my == 0.0f) && (mz == 0.0f)) { MahonyAHRSupdateIMU(gx, gy, gz, ax, ay, az); return; } // Compute feedback only if accelerometer measurement valid (avoids NaN in accelerometer normalisation) // 只在加速度计数据有效时才进行运算 if(!((ax == 0.0f) && (ay == 0.0f) && (az == 0.0f))) { // Normalise accelerometer measurement // 将加速度计得到的实际重力加速度向量v单位化 recipNorm = invSqrt(ax * ax + ay * ay + az * az); ax *= recipNorm; ay *= recipNorm; az *= recipNorm; // Normalise magnetometer measurement // 将磁力计得到的实际磁场向量m单位化 recipNorm = invSqrt(mx * mx + my * my + mz * mz); mx *= recipNorm; my *= recipNorm; mz *= recipNorm; // Auxiliary variables to avoid repeated arithmetic // 辅助变量,以避免重复运算 q0q0 = q0 * q0; q0q1 = q0 * q1; q0q2 = q0 * q2; q0q3 = q0 * q3; q1q1 = q1 * q1; q1q2 = q1 * q2; q1q3 = q1 * q3; q2q2 = q2 * q2; q2q3 = q2 * q3; q3q3 = q3 * q3; // Reference direction of Earth's magnetic field // 通过磁力计测量值与坐标转换矩阵得到大地坐标系下的理论地磁向量 hx = 2.0f * (mx * (0.5f - q2q2 - q3q3) + my * (q1q2 - q0q3) + mz * (q1q3 + q0q2)); hy = 2.0f * (mx * (q1q2 + q0q3) + my * (0.5f - q1q1 - q3q3) + mz * (q2q3 - q0q1)); bx = sqrt(hx * hx + hy * hy); bz = 2.0f * (mx * (q1q3 - q0q2) + my * (q2q3 + q0q1) + mz * (0.5f - q1q1 - q2q2)); // Estimated direction of gravity and magnetic field // 将理论重力加速度向量与理论地磁向量变换至机体坐标系 halfvx = q1q3 - q0q2; halfvy = q0q1 + q2q3; halfvz = q0q0 - 0.5f + q3q3; halfwx = bx * (0.5f - q2q2 - q3q3) + bz * (q1q3 - q0q2); halfwy = bx * (q1q2 - q0q3) + bz * (q0q1 + q2q3); halfwz = bx * (q0q2 + q1q3) + bz * (0.5f - q1q1 - q2q2); // Error is sum of cross product between estimated direction and measured direction of field vectors // 通过向量外积得到重力加速度向量和地磁向量的实际值与测量值之间误差 halfex = (ay * halfvz - az * halfvy) + (my * halfwz - mz * halfwy); halfey = (az * halfvx - ax * halfvz) + (mz * halfwx - mx * halfwz); halfez = (ax * halfvy - ay * halfvx) + (mx * halfwy - my * halfwx); // Compute and apply integral feedback if enabled // 在PI补偿器中积分项使能情况下计算并应用积分项 if(twoKi > 0.0f) { // integral error scaled by Ki // 积分过程 integralFBx += twoKi * halfex * (1.0f / sampleFreq); integralFBy += twoKi * halfey * (1.0f / sampleFreq); integralFBz += twoKi * halfez * (1.0f / sampleFreq); // apply integral feedback // 应用误差补偿中的积分项 gx += integralFBx; gy += integralFBy; gz += integralFBz; } else { // prevent integral windup // 避免为负值的Ki时积分异常饱和 integralFBx = 0.0f; integralFBy = 0.0f; integralFBz = 0.0f; } // Apply proportional feedback // 应用误差补偿中的比例项 gx += twoKp * halfex; gy += twoKp * halfey; gz += twoKp * halfez; } // Integrate rate of change of quaternion // 微分方程迭代求解 gx *= (0.5f * (1.0f / sampleFreq)); // pre-multiply common factors gy *= (0.5f * (1.0f / sampleFreq)); gz *= (0.5f * (1.0f / sampleFreq)); qa = q0; qb = q1; qc = q2; q0 += (-qb * gx - qc * gy - q3 * gz); q1 += (qa * gx + qc * gz - q3 * gy); q2 += (qa * gy - qb * gz + q3 * gx); q3 += (qa * gz + qb * gy - qc * gx); // Normalise quaternion // 单位化四元数 保证四元数在迭代过程中保持单位性质 recipNorm = invSqrt(q0 * q0 + q1 * q1 + q2 * q2 + q3 * q3); q0 *= recipNorm; q1 *= recipNorm; q2 *= recipNorm; q3 *= recipNorm; //Mahony官方程序到此结束,使用时只需在函数外进行四元数反解欧拉角即可完成全部姿态解算过程 }
1.5 互补滤波的思考
2023/4/14补充:该贴吧还介绍了一个比较重要的内容(同时也是下面需要介绍的):该贴吧谈到:
首先,对于六轴数据,计算角度有两种方法,一种是通过对角速度积分得到角度,另一种则是通过对加速度进行正交分解得到角度。但这两种方式均存在不足,通过角速度积分得到角度时,角速度的误差会在积分过程中被不断放大从而影响数据准确性。而加速度计是一种特别敏感的传感器,电机旋转产生的震动会给加速度计的数据中带来高频噪声。
不难看出,第一种方法测得的数据中存在结果偏差,而第二种方法测得的数据中存在高频噪声。因此可通过融合两种数据以获得准确姿态,这里通过加速度计补偿角速度。
2023/4/14补充
感谢博客(补充了后面的位姿递推):(80条消息) Mahony姿态解算算法详解_mahony算法_白鸟无言的博客-CSDN博客
上述Mahony算法还存在一个很大的误区点:
说透互补滤波(1) - 线性互补滤波器从原理到实现 - 知乎 (zhihu.com)
Mahony算法的核心在于:加速度计带有低频噪声,陀螺仪带有高频噪声(也可以理解为加速度信号对高频敏感,陀螺仪信号对低频敏感,不敏感效果就差了呗),所以我们把他们的噪声分别滤除,然后合并,就得到了没有噪声的原始信号。
但是实际你会发现两组数据其实在结算的时候只能使用一组:平衡情况下使用[0 0 g]T实现位姿求取,但是陀螺仪只有在发生转动的时候才能有数据,所以陀螺仪无法提供初始状态angle0。更可怕的是不平衡情况下(也就是运动情况下)只有陀螺仪一组数据能用,加速度计完全用不了。
就像贴吧说的那样:连两路输入都没有,还怎么互补滤波?所以在使用的互补滤波概念的时候是做了一个假设(参考上述博客):

之后关于低通滤波还有高通滤波这里就不细说了,贴吧还详细介绍了一、二阶低通滤波的原理,这部分估计要下次研究看到具体代码才能研究透彻了。(待续......)
二、卡尔曼滤波
2023/6/23日(3023/8/5修正)补充:卡尔曼在应用的时候需要注意:
- 从原理上来说,如果你对惯性导航的(位置、速度)误差进行建模是不行的,因为没有观测值Z,所以一般都是用组合导航的方式,常见的有GINS。纯惯导要注意最好别这样建模(倒是见到事后拿真实轨迹与推算的误差作为观测Z进行位置分析的)。(这里仍然有一定的怪怪的感觉,有想法可以评论交流一下)
- 卡尔曼应用于位姿滤波是可以的,有点像互补滤波,位姿主要使用的是陀螺仪,通过加速度计数据作为观测Z就能够修正估计量(陀螺仪数据)
- 互补滤波对于一些简单的计算精度就已经足够了,但是更好的就是卡尔曼了。
2.1 卡尔曼滤波公式推导
在上课的时候经常看到卡尔曼滤波的公式,尤其是考试的时候背的都烂了,但是在应用的时候还是不太会,趁这个时间,准备好好理解一下。下图是在课上经常看到的卡尔曼滤波五个公式:

在IMU实际应用解算的时候,会发现和上面公式多了几步或者有些出入。但大体是差不多了。
接下来就是阐述卡尔曼滤波的过程
(图片有些多,内容来源TKJ电子 » 卡尔曼滤波的实用方法及其实现方法 (tkjelectronics.dk))
让你直接看推导你是肯定接受不了的,所以要先文字叙述一下,你才能接受。由于公式编辑的麻烦,这部分我先在word中编译之后在贴图展示:


2.2 位姿推算的卡尔曼
后面推导就需要参考深度解析卡尔曼滤波在IMU中的使用 - 知乎 (zhihu.com)了,直接给出相关的代码(注意:这里仅仅是做位姿对陀螺仪Gyro进行建模,x就是位姿(角度),z就是陀螺仪(角速度)、没有使用加速度计信息Accel,加速度计也是可以使用的):
还可以参考
https://github.com/TKJElectronics/KalmanFilter/blob/master/Kalman.cpp在姿态估计中,我们希望通过使用传感器测量的角速度来估计物体的姿态(角度)。角速度通常是由陀螺仪等传感器提供的。
卡尔曼滤波器在姿态估计中的应用步骤如下:
状态向量定义:首先定义系统的状态向量,其中包括物体的姿态角度和角速度。在简单的二维情况下,状态向量可以表示为 [角度, 角速度]。
状态转移模型:建立系统的状态转移模型,描述状态如何随时间演化。在姿态估计中,我们可以使用物体的角速度来更新姿态角度。这里通常使用角速度积分来估计角度的变化。
观测模型:定义观测模型,将状态变量映射到传感器测量值。在这种情况下,观测模型将角速度映射到传感器测量的角速度。
卡尔曼增益:计算卡尔曼增益,它用于调整状态估计值和传感器测量值之间的权重。
预测步骤:通过使用状态转移模型进行预测,得到下一时刻的状态估计。
更新步骤:使用卡尔曼增益将预测值与传感器测量值进行融合,得到最终的姿态估计。
重复:重复预测和更新步骤,以实现实时姿态估计。
目前网上主流的就是这种位姿估计
2.3 位置推算下的卡尔曼
这部分不做过多的解释
参考:GitHub - i2Nav-WHU/KF-GINS: An EKF-Based GNSS/INS Integrated Navigation System
即武大KF-GINS
首先是构建离散卡尔曼滤波第一步的公式

我们是通过IMU的误差来建立状态方程(含义自己看pdf)
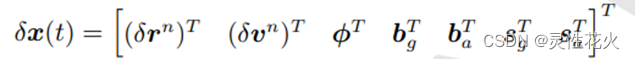
21维 3位置 3速度 3姿态 3陀螺仪零偏 3加速度计零偏 3陀螺仪+3加速度计比例因子误差
以及通过GNSS给出来的速度和位置作为观测

也就是PDF后面推导的公式:
![]()
![]()
后面就不洗细谈了,就是组合导航方向的了









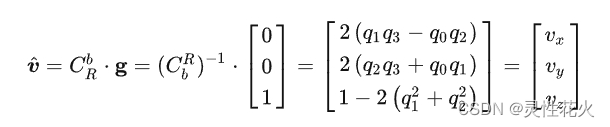





















 1501
1501

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








