Extended Kalman Filter(扩展卡尔曼滤波)是卡尔曼滤波的非线性版本。在状态转移方程确定的情况下,EKF已经成为了非线性系统状态估计的事实标准。本文将简要介绍EKF,并介绍其在无人驾驶多传感器融合上的应用。
KF与EKF
本文假定读者已熟悉KF,若不熟悉请参考卡尔曼滤波简介。
KF与EKF的区别如下:
- 预测未来:
x′=Fx+u
用
x′=f(x,u)
代替;其余
F
用
Fj 代替。 - 修正当下:将状态映射到测量的
Hx′
用
h(x′)
代替;其余
H
用
Hj 代替。
其中,非线性函数 f(x,u),h(x′) 用非线性得到了更精准的状态预测值、映射后的测量值;线性变换 Fj,Hj 通过线性变换使得变换后的 x,z 仍满足高斯分布的假设。
Fj,Hj 计算方式如下:
为什么要用EKF
KF的假设之一就是高斯分布的
x
预测后仍服从高斯分布,高斯分布的
将非线性系统线性化
既然非线性系统不行,那么很自然的解决思路就是将非线性系统线性化。
对于一维系统,采用泰勒一阶展开即可得到:
对于多维系统,仍旧采用泰勒一阶展开即可得到:
其中, Df(a) 是Jacobian矩阵。
多传感器融合
lidar与radar
本文将以汽车跟踪为例,目标是知道汽车时刻的状态 x=(px,py,vx,vy) 。已知的传感器有lidar、radar。
- lidar:笛卡尔坐标系。可检测到位置,没有速度信息。其测量值 z=(px,py) 。
- radar:极坐标系。可检测到距离,角度,速度信息,但是精度较低。其测量值 z=(ρ,ϕ,ρ˙) ,图示如下。
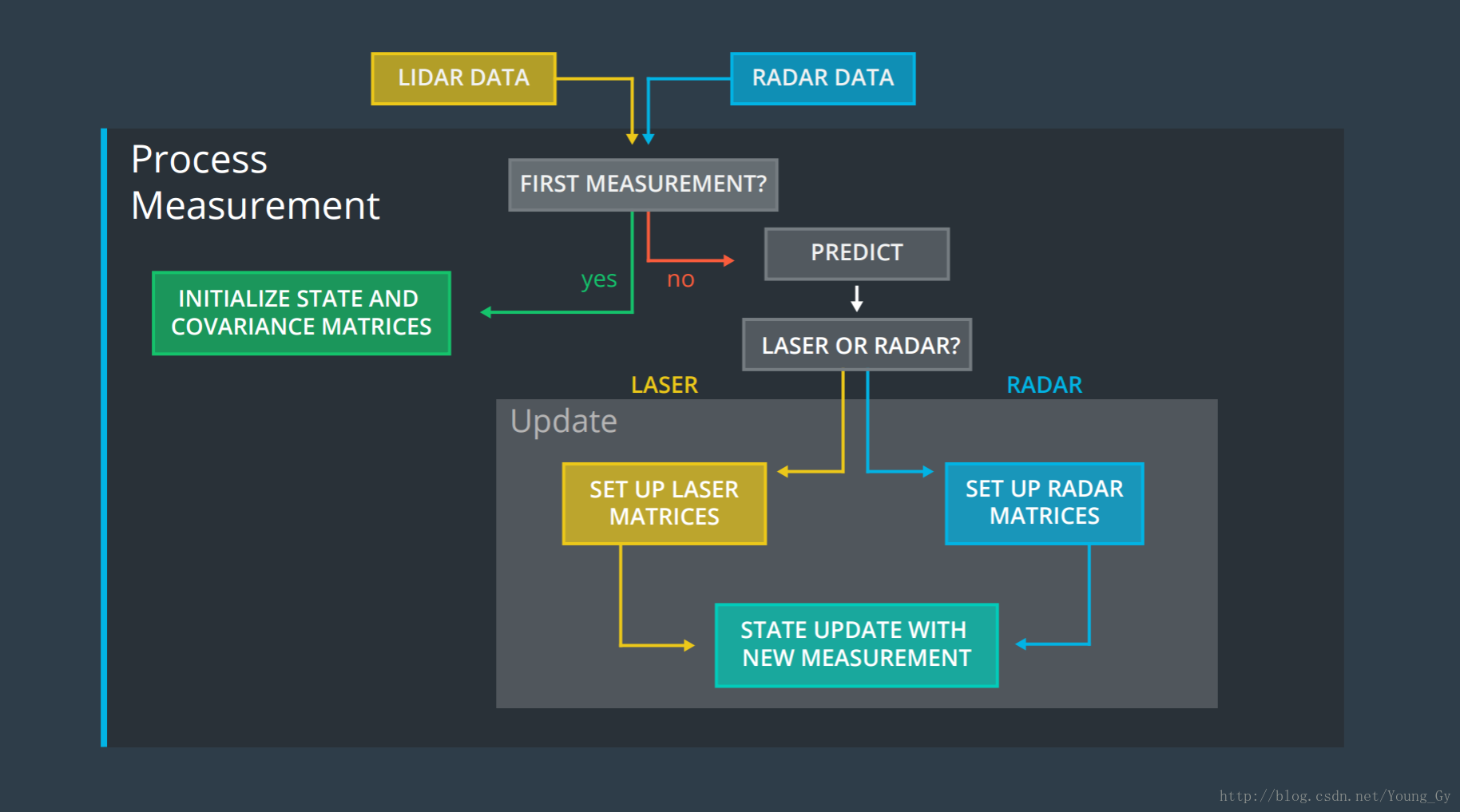
传感器融合步骤
步骤图如上所示,包括:
- 收到第一个测量值,对状态 x 进行初始化。
- 预测未来
- 修正当下
初始化
初始化,指在收到第一个测量值后,对状态
对于radar来说,
对于radar来说,
预测未来
预测主要涉及的公式是:
需要求解的有三个变量: F、P、Q 。
F 表明了系统的状态如何改变,这里仅考虑线性系统,F易得:
P
表明了系统状态的不确定性程度,用
Q
表明了
v
服从高斯分布
修正当下
lidar
lidar使用了KF。修正当下这里牵涉到的公式主要是:
需要求解的有两个变量: H、R 。
H 表示了状态空间到测量空间的映射。
R 表示了测量值的不确定度,一般由传感器的厂家提供,这里lidar参考如下:
radar
radar使用了EKF。修正当下这里牵涉到的公式主要是:
区别与上面lidar的主要有:
- 状态空间到测量空间的非线性映射 f(x)
- 非线性映射线性化后的Jacob矩阵
- radar的 Rradar
状态空间到测量空间的非线性映射 f(x) 如下
非线性映射线性化后的Jacob矩阵 Hj
R 表示了测量值的不确定度,一般由传感器的厂家提供,这里radar参考如下:
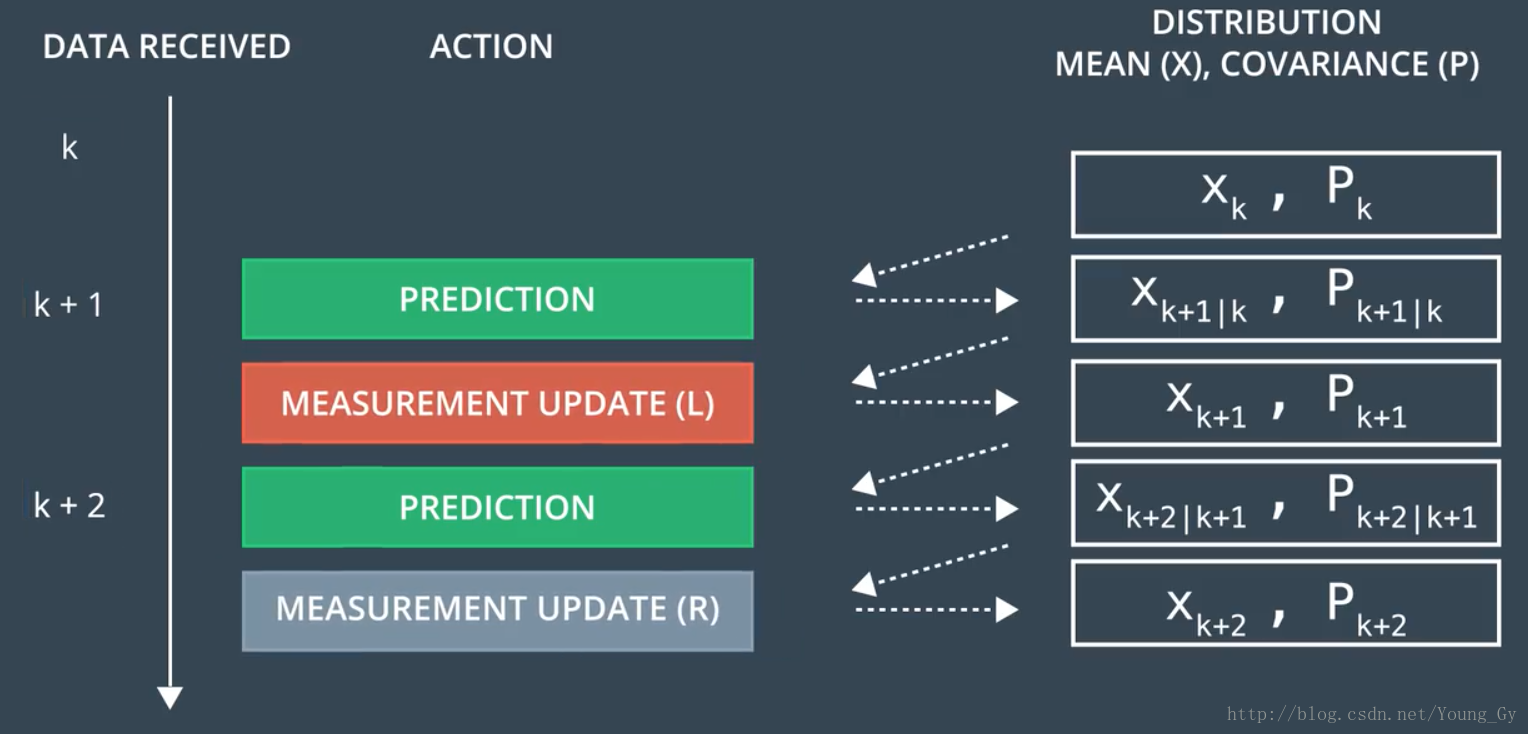
传感器融合实例
多传感器融合的示例如下,需要注意的有:
- lidar和radar的预测部分是完全相同的
- lidar和radar的参数更新部分是不同的,不同的原因是不同传感器收到的测量值是不同的
- 当收到lidar或radar的测量值,依次执行预测、更新步骤
- 当同时收到lidar和radar的测量值,依次执行预测、更新1、更新2步骤
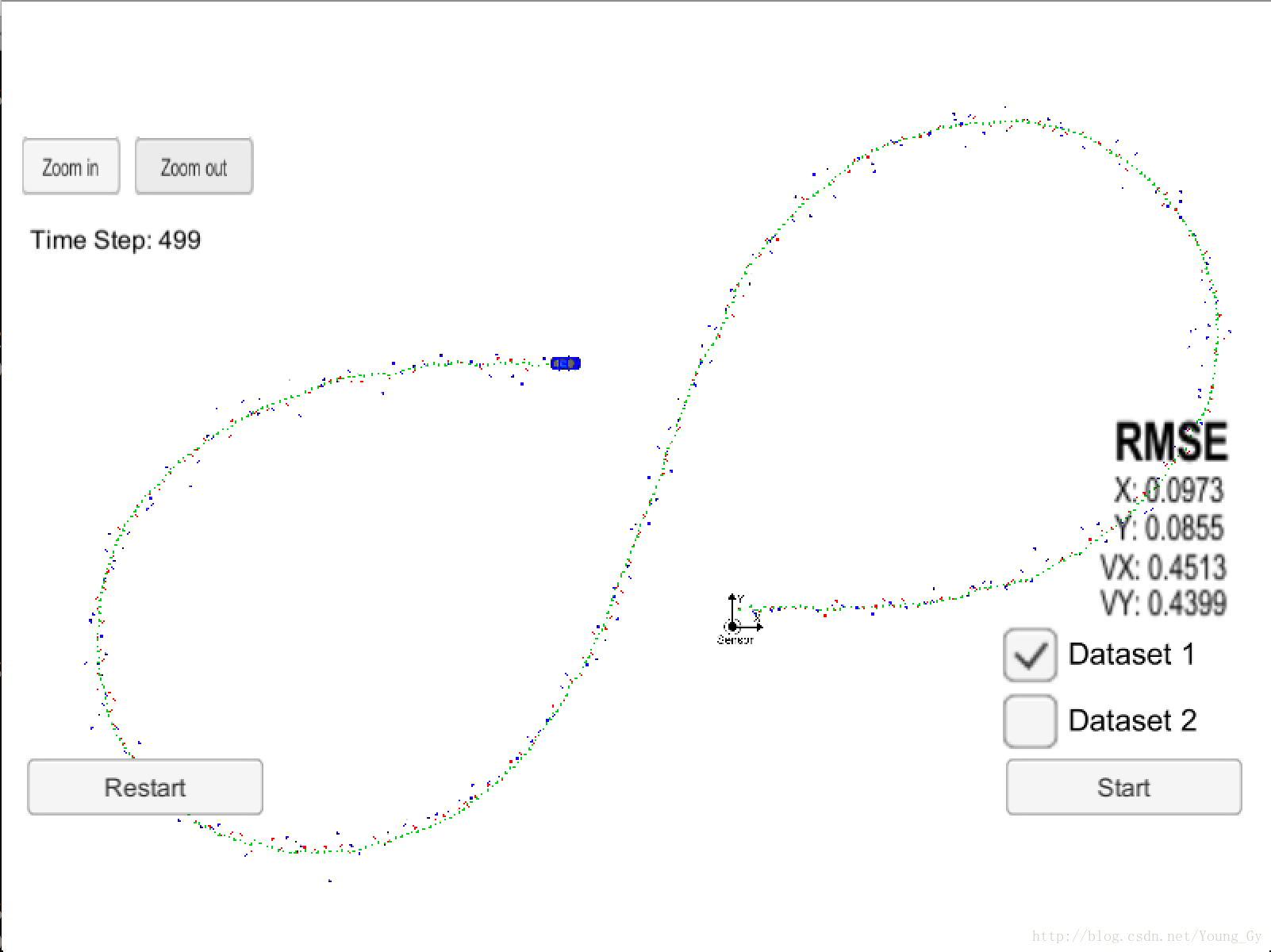
多传感器融合的效果如下图所示,红点和蓝点分别表示radar和lidar的测量位置,绿点代表了EKF经过多传感器融合后获取到的测量位置,取得了较低的RMSE。

























 1612
1612

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








