最小二乘法的概率解释

当我们面对回归问题时，为什么会采用线性回归，最小二乘法来定义成本函数，即1/2的差的平方和。

这里给出概率解释：

我们拟合的直线的函数值即预测值必然和真实值会存在误差。那么假定一个等式：

            

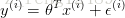
其中各个样本的误差项，是独立同分布且服从高斯分布（正态分布）。（可根据中心极限定理来看）

即就是：

                     

            

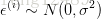
均值为0，容易理解.

所以，

            

也就是要面对 在以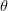为参数给定一个x时预测值y是真实值的概率服从正太分布，要求得概率最大时的？

最大似然估计：

            

            

            根据此过程，要求此函数的最大值 ，需求上式中后项函数  的最小值，

                   

            此函数又即为最小二乘估计的成本函数。

结论：上式推导即为最小二乘的概率解释。