连续傅里叶变换,拉普拉斯变换之间的关系以及理解
傅里叶转换公式:
如果要想该公式成立,需符合狄利赫里条件,即,所以这给傅里叶变换公式带来一定的局限性,它只适用于在定义域中收敛的函数,即只能分析稳定的系统!
如果我要分析一些不稳定的系统,即分析在定义域中不收敛的函数,该怎么办呢?
二.拉普拉斯变换
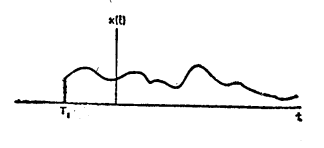
下图是一个在定义域内不收敛的右边信号,,很显然现在他不能用傅里叶变换公式去分析。
但是我能不能给他做一些函数变换,让它在定义中变得收敛,从而再用傅里叶变换去分析它呢!
答案是可以的!
因为总会有一个实指数信号乘以信号后,使其变得收敛,如下图,此时,这样我们岂不是就可以把这信号拿去给傅里叶变换公式分析了!
所以,当我们把信号带进傅里叶变换公式时,得到:
此时,使,得到:
上式即为拉普拉斯变换,换种说法,其就是一个信号与相乘后的傅里叶变换,即。
三.S平面
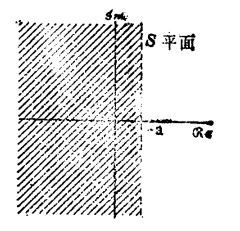
首先来介绍一下s平面:
(ps:在电子书上截图的,可能不是很清晰!)
我们知道,s平面的横坐标便是复数s的实部,纵坐标是虚部。
注意上图,我们可以把图中的阴影部分理解为由无数条一竖竖直线组成,那其中的一竖直线代表什么意思呢?
我们先在其中取一竖固定的直线,此时为一固定值,而则从到变化。
注意公式:
当为某一实数,信号为一确定信号,从而也确定了,此时s平面中与中的是相对应的,即s平面中的一竖直线对应某一种确定信号的傅里叶变换!
再来总结一下s平面:横坐标确定了某一信号,从而确定某一傅里叶变换。而纵坐标与傅里叶变换的定义域jw相对应。
四.收敛域问题
假设有一右边信号,让该信号做拉普拉斯变换,先乘以得到信号,想一下,此时当时,往右看,成增长趋势,并不是收敛函数。
因此,并不是所有的都使收敛。
所以,得出了收敛域的定义:在收敛域中,存在,使得为收敛函数。
下图为一右边信号,使等于某一实数,使得为收敛函数,如图:
此时,当时,衰减速度更快,从而可知也一定收敛。
所以可以得到拉普拉斯收敛的一个性质:
按照这个思路,我们也同理推出收敛的另一性质:
但如果是双边信号呢,我们可以把分解成一左边信号和右边信号,即
= + 。当 收敛时,也一定有 和 同时收敛,所以可知 的收敛域为 与 两者收敛域的重叠部分,如下图:所以可得到第三个收敛的性质:
五.总结
整篇文章主要讲了拉普拉斯变换过程,讲述了拉普拉斯与傅里叶变换的关系,讲述了s平面的含义以及叙述了拉普拉斯变换收敛域以及其中的三个主要性质。如果想要更详细了解拉普拉斯变换更多地性质,建议去阅读相关资料,由于时间关系,无法一一详细叙述。如有错误地方,希望可以指出,谢谢!









 我们知道
我们知道


 但如果
但如果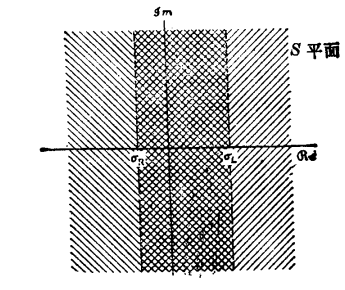














 1万+
1万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








