本文相对于摘抄的文章已经有大量的修改,如有阅读不适,请移步原文。
以下摘抄转自于维基:基于深度学习的图像识别进展百度的若干实践
从没有感知域(receptive field) 的深度神经网络,到固定感知域的卷积神经网络,再到可变感知域的递归神经网络,深度学习模型在各种图像识别问题中不断演进。
曾经爆炸式增长的参数规模逐步得到有效控制,人们将关于图像的先验知识逐渐用于深度学习,大规模并行化计算平台愈加成熟,这些使我们能够从容应对大数据条件下的图像识别问题。
CNN的二维处理递进结构天然适合图像处理,直接把图像模式识别问题从特征提取-模式识别压缩为模式识别一步完成,和传统模式识别方法框架上都已经有了本质的区别。
用于ImageRecognition的CNN:
参考链接:http://blog.csdn.net/zouxy09/article/details/8781543/
维基解释:卷积神经网络(Convolutional Neural Network)由一个或多个卷积层和顶端的全连通层(对应经典的神经网络)组成,同时也包括关联权重和池化层(pooling layer)。这一结构使得卷积神经网络能够利用输入数据的二维结构。
与其他深度学习结构相比,卷积神经网络在图像和语音识别方面能够给出更优的结果。这一模型也可以使用反向传播算法进行训练。相比较其他深度、前馈神经网络,卷积神经网络需要估计的参数更少,使之成为一种颇具吸引力的深度学习结构[2]。
卷积网络是为识别二维形状而特殊设计的一个多层感知器,这种网络结构对平移、比例缩放、倾斜或者共他形式的变形具有高度不变性。
特点:它的权值共享网络结构使之更类似于生物神经网络,降低了网络模型的复杂度,减少了权值的数量。该优点在网络的输入是多维图像时表现的更为明显,使图像可以直接作为网络的输入,避免了传统识别算法中复杂的特征提取和数据重建过程。
CNNs是受早期的延时神经网络(TDNN)的影响。延时神经网络通过在时间维度上共享权值降低学习复杂度,适用于语音和时间序列信号的处理,而CNNs在空间维度上使用权值共享降低学习复杂度。
但CNNs是第一个真正成功训练多层网络结构的学习算法。它利用空间关系减少需要学习的参数数目以提高一般前向BP算法的训练性能。CNNs作为一个深度学习架构提出是为了最小化数据的预处理要求。在CNN中,图像的一小部分(局部感受区域)作为层级结构的最低层的输入,信息再依次传输到不同的层,每层通过一个数字滤波器去 获得观测数据的最显著的特征 。这个方法能够获取对平移、缩放和旋转不变的观测数据的显著特征,因为图像的局部感受区域允许神经元或者处理单元可以访问到最基础的特征,例如定向边缘或者角点。
小盆友1视野很小,每个感受野对应一些参数,假设为w1w2w3w4,每滑动一次,另一个感受野又对应四个w,因为每个小朋友都有自己处事原则(不管看什么,参数不变),所以一个小盆友只要学习四个参数。一幅图只要4*5=20个参数 开个玩笑,如果小盆友都很善变,每次看东西方式都变,会有height_col*width_col*4*5个参数啊!计算量很大。
文章:理解参数共享
注: int height_col= (height + 2 * pad_h - kernel_h) / stride_h + 1;
int width_col = (width + 2 * pad_w - kernel_w) / stride_w + 1;
一、CNN用于特征学习?参数!
参考链接:http://www.open-open.com/lib/view/open1425626861103.html
在图像处理中,往往把图像表示为像素的向量,比如一个1000×1000的图像,可以表示为一个1000000的向量(但这种说法是极为不确切的,X维和Y维的像素意义完全不同。应该说1000*1000的图像,转化到一维欧式空间之后,映射到1000000维向量空间的基上)。在一般神经网络 中,如果隐含层神经元数目与输入层一样,即也是1000000时,那么输入层到隐含层的参数数据为1000000×1000000=10^12,这样就太多了, 基本没法训练。所以图像处理要想练成神经网络大法,必先减少参数加快速度。
(对于传统ML方法,特征是什么?特征是特征提取函数(特征hash,即图像从二维欧式空间转化为N维向量空间的hash映射)提取的N维向量,把信息从二维图像空间压缩到一维欧式空间的N维向量空间。而对于CNN,特征这个定义已经没有意义,到底前面哪些层得到的结果可以称为特征,后面哪些层属于分类器,已经不好定论。而对于整个CNN过程,一般不会出现欧式维度降低的现象,几乎都是二维图像在不停的Pooling和Conv,知道最后收敛到1*1,即可以认为是二维点,也可以认为是一维点,这就是模式识别的最终结果,那个0和1)
当然,图像的输入尺度一般不会达到1000分辨率,而达到较好的训练效果,却实在需要更多层的网络,这样仍会产生更多的参数。此外,对CNN也有识别图像旋转和尺度不变性的要求。
卷积神经网络有两种神器可以降低参数数目,第一种神器叫做局部感知野,第二种为权值共享,此外还有图像下采样。
1.局部感受野 Local Receptive Area / Fiileds
一般感知信息的联系为局部到全局,而图像的空间联系也是局部像素 联系较为紧密,而距离较远的像素相关性较弱。因而,每个神经元其实没有必要对全局图像进行感知,只需要对局部进行感知,然后在更高层将局部的信息综合起 来就得到全局信息。
局部神经元和局部神经元链接,网络部分连通的思想,也是受启发于生物学里面的视觉系统结构。视觉皮层的神经元就是局部接受信息的(即这些神经元只响应某些特定区 域的刺激),也就是所谓的局部感受野。
(一般意义上,全连接的除了某个局部,其他部分参数已经为0,那么这个不为0的局部,也就成为了局部感受野 )
)
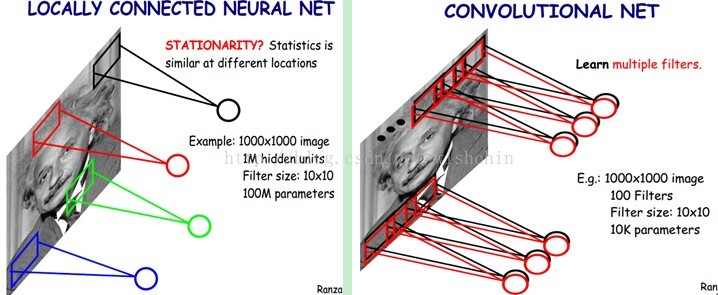
如下图所示:左图为全连接,右图为局部连接。

多层网络实现局部关联
在上右图中,假如每个神经元只和10×10个像素值相连,那么权值数据为1000000×100个参数,减少为原来的千分之一。而那10×10个像素值对应的10×10个参数,其实就相当于卷积操作,因此为卷积神经网络。
其对应结构为
卷积层:卷积神经网络中每层卷积层由若干卷积单元组成,每个卷积单元的参数都是通过反向传播算法优化得到的。卷积运算的目的是提取输入的不同特征,第一层卷积层可能只能提取一些低级的特征如边缘、线条和角等层级,更多层的网络能从低级特征中迭代提取更复杂的特征(这也是深度的要求)。
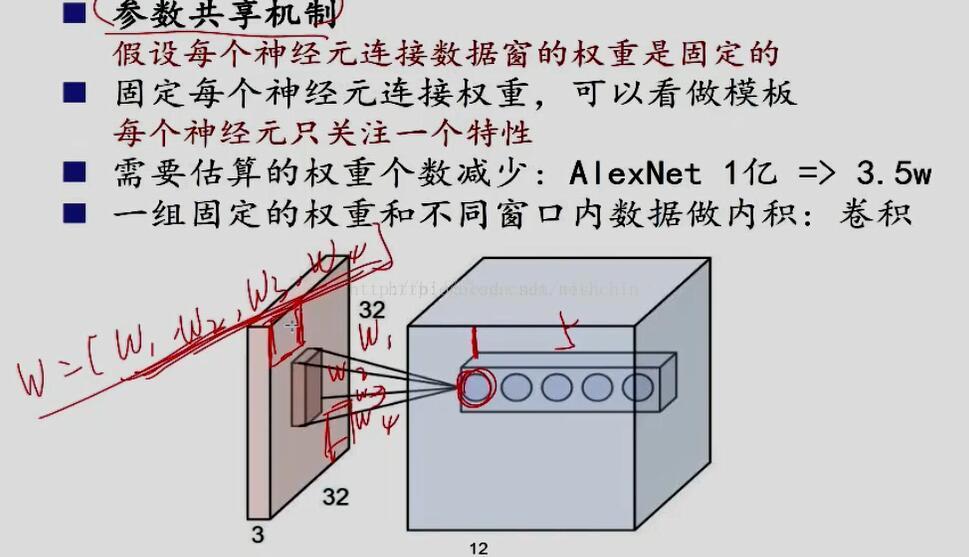
2.参数共享shared Weights—那个滑动的卷积核
但其实这样的话参数仍然过多,那么就启动第二级参数降低方法,即权值共享。实现方法呢?即是使用共享卷积核。那一层只学习一个卷积核,或者在某个局部共享卷积核,这就成了下面图中,那个滑动的核........其实核没有滑动,只是参数是一样的,看起来就像是滑动卷积过程。
怎么理解权值共享呢?网络中每个神经元都链接10*10的图像区域,我们可以这100个参数(也就是卷积操作)看成是提取特征的方式,该方式与位置无关。
CNN在在上面的局部连接中,一共1000000个神经元,每个神经元都链接10*10 的图像区域,即对应100个参数。但对于这1000000个神经元,若每个神经元的这100个参数都是相等的,即是每个神经元用同一个卷积核去卷积图像局部,那么参数数目就变为100了。
不管隐层的神经元个数有多少,两层间的连接只有100个参数,这就是CNNs的主要卖点。直接对应了特征选择中的稀疏编码,降低特征空间。
这其中隐含原理则是:图像的一部分的统计特性与其他部分是一样的。这也意味着我们在这一部分学习的特征也能用在另一部分上,所以对于这个图像上的所有位置,我们都能使用同样的学习特征,则表现为权值是共享的。
图2.1 权值共享
更直观一些,当从一个大尺寸图像中随机选取一小块,比如说 8×8 作为样本,并且从这个小块样本中学习到了一些特征,这时我们可以把从这个 8×8 样本中学习到的特征作为探测器,应用到这个图像的任意地方中去。特别是,我们可以用从 8×8 样本中所学习到的特征跟原本的大尺寸图像作卷积,从而对这个大尺寸图像上的任一位置获得一个不同特征的激活值。
悲剧的地方:这个共享卷积核其实只是学习了一个特征,那怎么能行呢?没关系!CNN是多层的神经网络,Deep的意义就是实现复合函数比单联通函数更少遍历而更多选择的功能,净多多次复合可以得到多种可能的效果,意思就是用多层多个卷积核实现单层多个卷积核的功能 。
。
如下图所示,展示了一个3*3的卷积核在5*5的图像上做卷积的过程。每个卷积都是一种特征提取方式,就像一个筛子,将图像中符合条件(激活值越大越符合条件)的部分筛选出来。
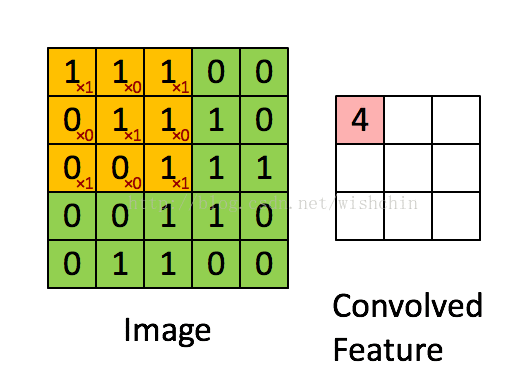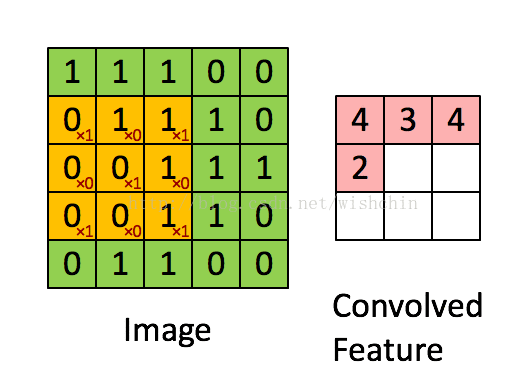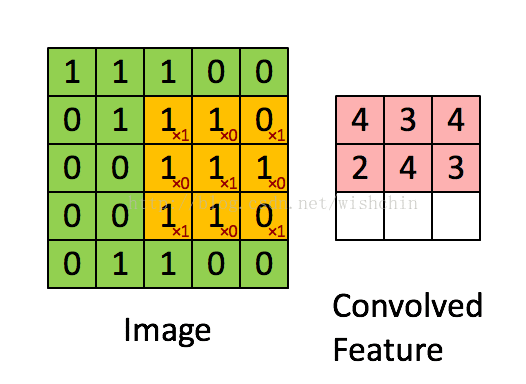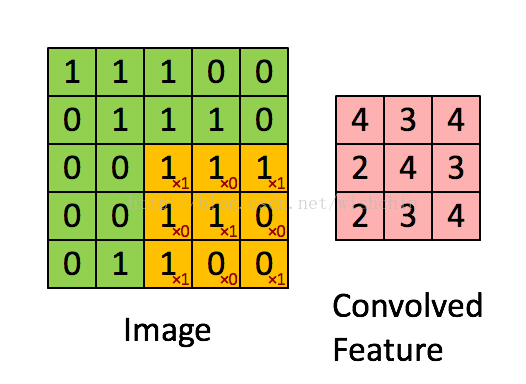
图2.2 权值共享/特征共享
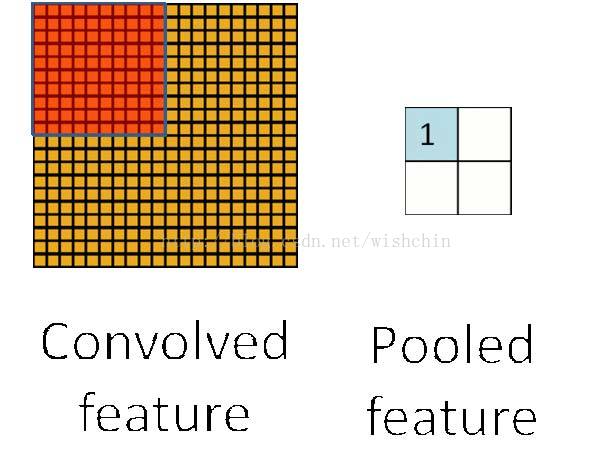
3. 空间降采样
在通过卷积获得了特征 (features) 之后,下一步我们希望利用这些特征去做分类。理论上讲,人们可以用所有提取得到的特征去训练分类器,例如 softmax 分类器,但这样做面临计算量的挑战。例如:对于一个 96X96 像素的图像,假设我们已经学习得到了400个定义在8X8输入上的特征,每一个特征和图像卷积都会得到一个 (96 − 8 + 1) × (96 − 8 + 1) = 7921 维的卷积特征,由于有 400 个特征,所以每个样例 (example) 都会得到一个 892 × 400 = 3,168,400 维的卷积特征向量。学习一个拥有超过 3 百万特征输入的分类器十分不便,需要训练相当多的参数,并且容易出现过拟合 (over-fitting)。
为了解决这个问题,首先回忆一下,我们之所以决定使用卷积后的特征是因为图像具有一种“静态性”的属性,这也就意味着在一个图像区域有用的特征极 有可能在另一个区域同样适用。因此,为了描述大的图像,一个很自然的想法就是对不同位置的特征进行聚合统计,例如,人们可以计算图像一个区域上的某个特定 特征的平均值 (或最大值)。这些概要统计特征不仅具有低得多的维度 (相比使用所有提取得到的特征),参数减少,同时还会改善结果(不容易过拟合)。这种聚合的操作就叫做池化 (pooling),有时也称为平均池化或者最大池化 (取决于计算池化的方法)。
线性整流层:使用ReLU函数或者tanh函数
池化层:
图3.1 特征池化层(空间降采样)
4. 终止层:终止层用于防止过拟合。
随机丢失:使用随机性,用以爬出局部最优区域.
Dropout "layer":
Since a fully connected layer occupies most of the parameters, it is prone tooverfitting. The dropout method[19] is introduced to prevent overfitting. Dropout also significantly improves the speed of training. This makes model combination practical, even for deep neural nets. Dropout is performed randomly. In the input layer, the probability of dropping a neuron is between 0.5 and 1, while in the hidden layers, a probability of 0.5 is used. The neurons that are dropped out, will not contribute to the forward pass and back propagation. This is equivalent to decreasing the number of neurons. This will create neural networks with different architectures, but all of those networks will share the same weights.
The biggest contribution of the dropout method is that, although it effectively generates 2^n neural nets, with different architectures (n=number of "droppable" neurons), and as such, allows for model combination, at test time, only a single network needs to be tested. This is accomplished by performing the test with the un-thinned network, while multiplying the output weights of each neuron with the probability of that neuron being retained (i.e. not dropped out).
损失层:
Loss layer:损失函数的确定是重点......一般多类识别默认使用了SoftMax函数,而损失函数又怎么选择呢?
It can use different loss functions for different tasks. Softmax loss is used for predicting a single class of K mutually exclusive classes. Sigmoid cross-entropy loss is used for predicting K independent probability values in [0,1]. Euclidean loss is used for regressing to real-valued labels [-inf,inf]
二、CNN普遍应用形式
基于其三个特点:
• Local connectivity: 局部特征的响应
• Parameter sharing: 减小参数个数——对局部特征的平移不变性
• pooling/subsampling hidden units: 减小参数的个数——对局部特征的旋转不变性产生影响
三、CNN的不断改进:
• 输入 数据: data distortion, generating additional examples, trasfer learning, big data...
• 隐层节点输入: Dopconnect, Maxout...
• 隐层 节点: sigmoid, tanh, linear, ReLU(这个很重要)...
• 隐层节点输出: Dropout...
• 卷 积: receptive field size, overlap or not...
• 池 化: mean-pooling均值, max-pooling最大, Stochastic pooling随机, 3D pooling三维收敛, linear or not线性或非线性...
• 网络 结构: layer’s connect way, #hidden units, #layers(deep learning)...
• 优化 方法: pre-training预训练, fine-tunning微调, learning rate学习率, moment, mini-batch设定批大小, sgd随机梯度下降, hessin free...
• 规则项、大脑皮层、理论研究...
这里面每一个方法都值得好好考虑,并深入研究........
四、微调(fine-tuning)
类似于始祖DNN论文里面所使用的使用大量的非监督学习数据来逐层训练调整网络结构,是极为费力的事情。一般工业级别CNN的使用方式是拿来一个在相似领域训练的超类网络,应用于自身数据集时进行微调,也能达到较好的效果。一般使用相同结构的使用ImageNet预训练过的CNN,其前面几层相当于已经训练好的特征提取网络,应用于相应的场景,只需要在后几层进行结构修改,并对前几层微调即可。
可用包
- Caffe: Caffe 包含了CNN使用最广泛的库。它由伯克利视觉和学习中心(BVLC)研发,拥有比一般实现更好的结构和更快的速度,分离的设定和执行。同时支持CPU和GPU计算,底层由C++实现,并封装了Python和MATLAB的接口。
- Torch7 (www.torch.ch)
- OverFeat
- Cuda-convnet
- MatConvnet
- Theano: 用Python实现的神经网络包[3]
五、CNN示例--从Lenet到AlexNet
此段请移步原文:卷积神经网络进化史:从Lenet到AlexNet
5.0:本系列博客是对刘昕博士的《CNN的近期进展与实用技巧》的一个扩充性资料。
主要讨论CNN的发展,并且引用刘昕博士的思路,对CNN的发展作一个更加详细的介绍,将按下图的CNN发展史进行描述:

上图所示是刘昕博士总结的CNN结构演化的历史,起点是神经认知机模型,此时已经出现了卷积结构,经典的LeNet诞生于1998年。然而之后CNN的锋芒开始被SVM等手工设计的特征盖过。随着ReLU和dropout的提出,以及GPU和大数据带来的历史机遇,CNN在2012年迎来了历史突破–AlexNet.
CNN的演化路径可以总结为以下几个方向:
- 从LeNet到AlexNet
- 进化之路一:网络结构加深
- 进化之路二:加强卷积功能
- 进化之路三:从分类到检测
- 进化之路四:新增功能模块
本系列博客将对CNN发展的四条路径中最具代表性的CNN模型结构进行讲解。
一切的开始(LeNet)
下图是广为流传LeNet的网络结构,麻雀虽小,但五脏俱全,卷积层、pooling层、全连接层,这些都是现代CNN网络的基本组件。

- 输入尺寸:32*32
- 卷积层:3个
- 降采样层:2个
- 全连接层:1个
- 输出:10个类别(数字0-9的概率)
因为LeNet可以说是CNN的开端,所以这里简单介绍一下各个组件的用途与意义。
Input (32*32)
输入图像Size为32*32。这要比mnist数据库中最大的字母(28*28)还大。这样做的目的是希望潜在的明显特征,如笔画断续、角点能够出现在最高层特征监测子感受野的中心。
C1, C3, C5 (卷积层)
卷积核在二维平面上平移,并且卷积核的每个元素与被卷积图像对应位置相乘,再求和。通过卷积核的不断移动,我们就有了一个新的图像,这个图像完全由卷积核在各个位置时的乘积求和的结果组成。
二维卷积在图像中的效果就是: 对图像的每个像素的邻域(邻域大小就是核的大小)加权求和得到该像素点的输出值。
具体做法如下:

卷积运算一个重要的特点就是: 通过卷积运算,可以使原信号特征增强,并且降低噪音。但同时也降低了精度。
不同的卷积核能够提取到图像中的不同特征,这里有在线demo,下面是不同卷积核得到的不同的feature map,

以C1层进行说明:C1层是一个卷积层,有6个卷积核(提取6种局部特征),核大小为5*5,能够输出6个特征图Feature Map,大小为28*28。C1有156个可训练参数(每个滤波器5*5=25个unit参数和一个bias参数,一共6个滤波器,共(5*5+1)6=156个参数),共156(28*28)=122,304个连接。
S2, S4 (pooling层)
S2, S4是下采样层,是为了降低网络训练参数及模型的过拟合程度。池化/采样的方式通常有以下两种:
- Max-Pooling: 选择Pooling窗口中的最大值作为采样值;
- Mean-Pooling: 将Pooling窗口中的所有值相加取平均,以平均值作为采样值;
S2层是6个14*14的feature map,map中的每一个单元于上一层的 2*2 领域相连接,所以,S2层是C1层的1/4。
F6 (全连接层)
F6是全连接层,类似MLP中的一个layer,共有84个神经元(为什么选这个数字?跟输出层有关),这84个神经元与C5层进行全连接,所以需要训练的参数是:(120+1)*84=10164.
如同经典神经网络,F6层计算输入向量和权重向量之间的点积,再加上一个偏置。然后将其传递给sigmoid函数产生单元i的一个状态。
Output (输出层)
输出层由欧式径向基函数(Euclidean Radial Basis Function)单元组成,每类一个单元,每个有84个输入。
换句话说,每个输出RBF单元计算输入向量和参数向量之间的欧式距离。输入离参数向量越远,RBF输出的越大。用概率术语来说,RBF输出可以被理解为F6层配置空间的高斯分布的负log-likelihood。给定一个输式,损失函数应能使得F6的配置与RBF参数向量(即模式的期望分类)足够接近。

LeNet5网络:http://yann.lecun.com/exdb/lenet/index.html
利用LeNet5网络,可以很快的搭建一个手写数字识别分类器。不妨试一下
王者回归(AlexNet)
AlexNet 可以说是具有历史意义的一个网络结构,可以说在AlexNet之前,深度学习已经沉寂了很久。历史的转折在2012年到来,AlexNet 在当年的ImageNet图像分类竞赛中,top-5错误率比上一年的冠军下降了十个百分点,而且远远超过当年的第二名。
AlexNet 之所以能够成功,深度学习之所以能够重回历史舞台,原因在于:
- 非线性激活函数:ReLU
- 防止过拟合的方法:Dropout,Data augmentation
- 大数据训练:百万级ImageNet图像数据
- 其他:GPU实现,LRN归一化层的使用
下面简单介绍一下AlexNet的一些细节:
Data augmentation
有一种观点认为神经网络是靠数据喂出来的,若增加训练数据,则能够提升算法的准确率,因为这样可以避免过拟合,而避免了过拟合你就可以增大你的网络结构了。当训练数据有限的时候,可以通过一些变换来从已有的训练数据集中生成一些新的数据,来扩大训练数据的size。
其中,最简单、通用的图像数据变形的方式:
- 从原始图像(256,256)中,随机的crop出一些图像(224,224)。【平移变换,crop】
- 水平翻转图像。【反射变换,flip】
- 给图像增加一些随机的光照。【光照、彩色变换,color jittering】

AlexNet 训练的时候,在data augmentation上处理的很好:
- 随机crop。训练时候,对于256*256的图片进行随机crop到224*224,然后允许水平翻转,那么相当与将样本倍增到((256-224)^2)*2=2048。
- 测试时候,对左上、右上、左下、右下、中间做了5次crop,然后翻转,共10个crop,之后对结果求平均。作者说,不做随机crop,大网络基本都过拟合(under substantial overfitting)。
- 对RGB空间做PCA,然后对主成分做一个(0, 0.1)的高斯扰动。结果让错误率又下降了1%。
ReLU 激活函数
Sigmoid 是常用的非线性的激活函数,它能够把输入的连续实值“压缩”到0和1之间。特别的,如果是非常大的负数,那么输出就是0;如果是非常大的正数,输出就是1.
但是它有一些致命的 缺点:
- Sigmoids saturate and kill gradients. sigmoid 有一个非常致命的缺点,当输入非常大或者非常小的时候,会有饱和现象,这些神经元的梯度是接近于0的。如果你的初始值很大的话,梯度在反向传播的时候因为需要乘上一个sigmoid 的导数,所以会使得梯度越来越小,这会导致网络变的很难学习。
- Sigmoid 的 output 不是0均值. 这是不可取的,因为这会导致后一层的神经元将得到上一层输出的非0均值的信号作为输入。
产生的一个结果就是:如果数据进入神经元的时候是正的(e.g. x>0 elementwise in f=wTx+b ),那么 w 计算出的梯度也会始终都是正的。
当然了,如果你是按batch去训练,那么那个batch可能得到不同的信号,所以这个问题还是可以缓解一下的。因此,非0均值这个问题虽然会产生一些不好的影响,不过跟上面提到的 kill gradients 问题相比还是要好很多的。
ReLU 的数学表达式如下:
很显然,从图左可以看出,输入信号 <0 时,输出都是0, >0 的情况下,输出等于输入。 w 是二维的情况下,使用ReLU之后的效果如下:

Alex用ReLU代替了Sigmoid,发现使用 ReLU 得到的SGD的收敛速度会比 sigmoid/tanh 快很多。
主要是因为它是linear,而且 non-saturating(因为ReLU的导数始终是1),相比于 sigmoid/tanh,ReLU 只需要一个阈值就可以得到激活值,而不用去算一大堆复杂的运算。
关于激活函数更多内容,请移步我的另一篇文章:激活函数-面面观
Dropout
结合预先训练好的许多不同模型,来进行预测是一种非常成功的减少测试误差的方式(Ensemble)。但因为每个模型的训练都需要花了好几天时间,因此这种做法对于大型神经网络来说太过昂贵。
然而,AlexNet 提出了一个非常有效的模型组合版本,它在训练中只需要花费两倍于单模型的时间。这种技术叫做Dropout,它做的就是以0.5的概率,将每个隐层神经元的输出设置为零。以这种方式“dropped out”的神经元既不参与前向传播,也不参与反向传播。
所以每次输入一个样本,就相当于该神经网络就尝试了一个新的结构,但是所有这些结构之间共享权重。因为神经元不能依赖于其他特定神经元而存在,所以这种技术降低了神经元复杂的互适应关系。
正因如此,网络需要被迫学习更为鲁棒的特征,这些特征在结合其他神经元的一些不同随机子集时有用。在测试时,我们将所有神经元的输出都仅仅只乘以0.5,对于获取指数级dropout网络产生的预测分布的几何平均值,这是一个合理的近似方法。
多GPU训练
单个GTX 580 GPU只有3GB内存,这限制了在其上训练的网络的最大规模。因此他们将网络分布在两个GPU上。 目前的GPU特别适合跨GPU并行化,因为它们能够直接从另一个GPU的内存中读出和写入,不需要通过主机内存。
他们采用的并行方案是:在每个GPU中放置一半核(或神经元),还有一个额外的技巧:GPU间的通讯只在某些层进行。

例如,第3层的核需要从第2层中所有核映射输入。然而,第4层的核只需要从第3层中位于同一GPU的那些核映射输入。
Local Responce Normalization
一句话概括:本质上,这个层也是为了防止激活函数的饱和的。
个人理解原理是通过正则化让激活函数的输入靠近“碗”的中间(避免饱和),从而获得比较大的导数值。所以从功能上说,跟ReLU是重复的。不过作者说,从试验结果看,LRN操作可以提高网络的泛化能力,将错误率降低了大约1个百分点。
AlexNet 优势在于:网络增大(5个卷积层+3个全连接层+1个softmax层),同时解决过拟合(dropout,data augmentation,LRN),并且利用多GPU加速运算。
六、深度图像之图像分类模型之Alexnet详细解读
CNN在图像处理与模式识别被证明有效性之后,Caffe横空出世,给Google这个绿茶婊一个重击。在imagenet上的图像分类challenge上Alex提出的alexnet网络结构模型赢得了2012届的冠军。要研究CNN类型DL网络模型在图像分类上的应用,就逃不开研究alexnet,这是CNN在图像分类上的经典模型(DL火起来之后)。
在DL开源实现caffe的model样例中,它也给出了alexnet的复现,具体网络配置文件如下https://github.com/BVLC/caffe/blob/master/models/bvlc_reference_caffenet/train_val.prototxt:
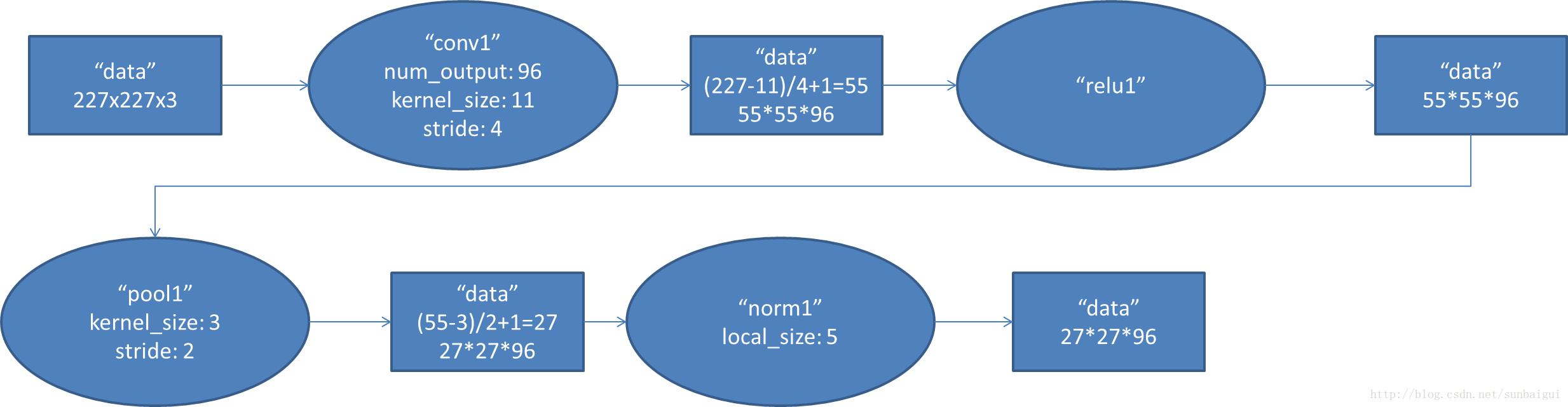
1. conv1阶段DFD(data flow diagram):
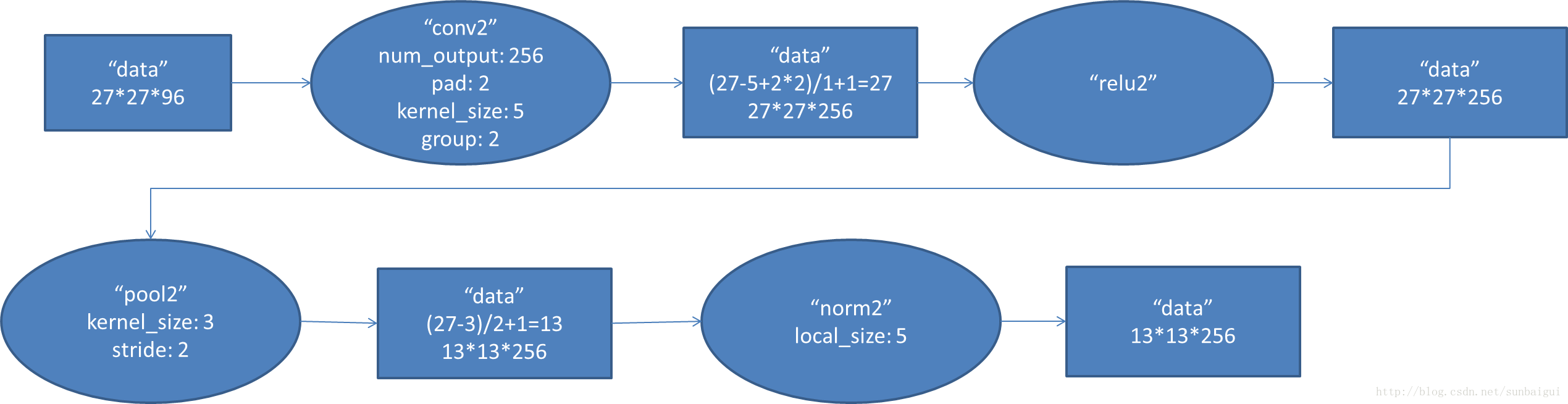
2. conv2阶段DFD(data flow diagram):
3. conv3阶段DFD(data flow diagram):
4. conv4阶段DFD(data flow diagram):
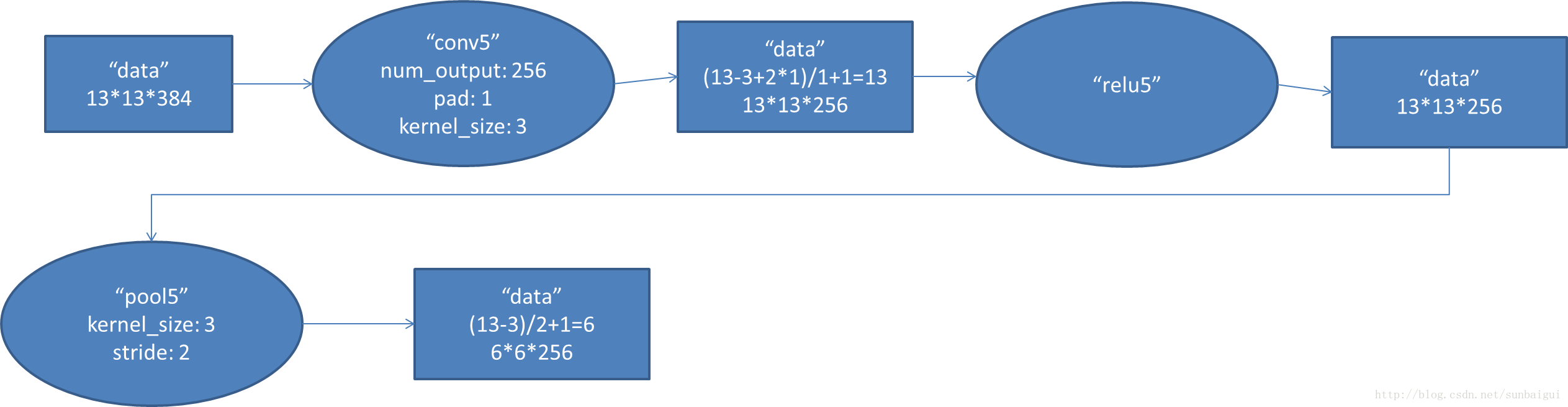
5. conv5阶段DFD(data flow diagram):
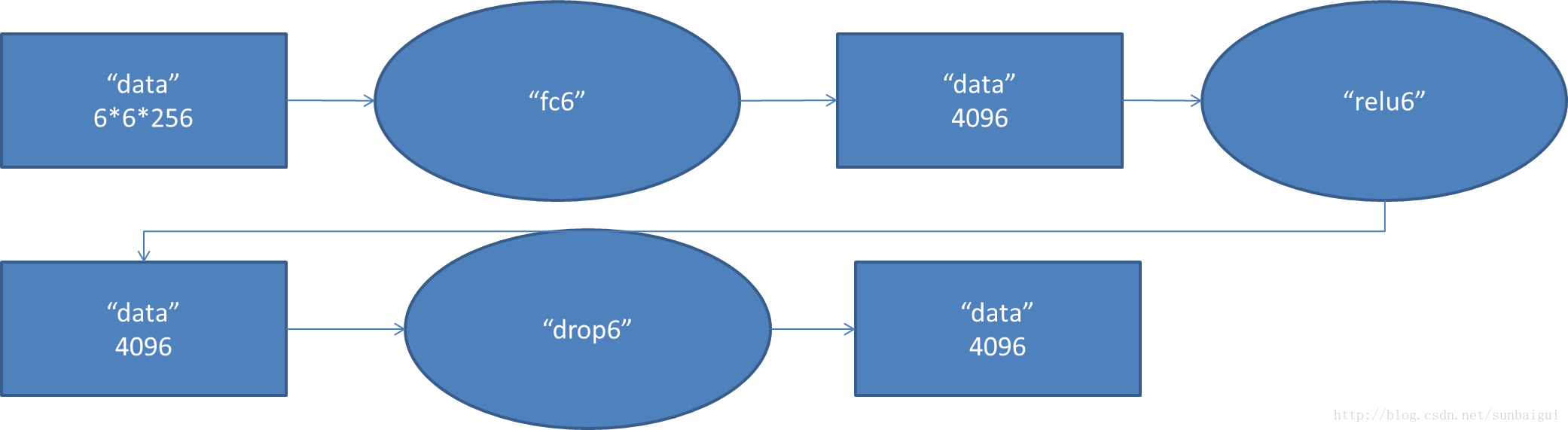
6. fc6阶段DFD(data flow diagram):
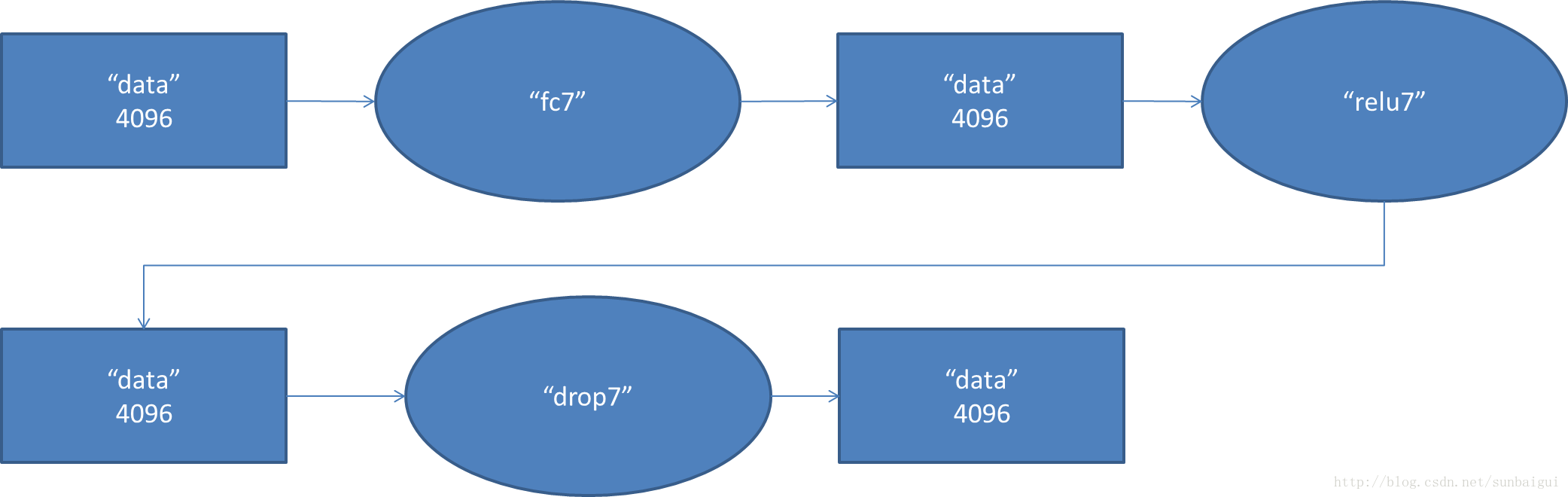
7. fc7阶段DFD(data flow diagram):
8. fc8阶段DFD(data flow diagram):
各种layer的operation更多解释可以参考:http://caffe.berkeleyvision.org/tutorial/layers.html
从计算该模型的数据流过程中,该模型参数大概5kw+。
caffe的输出中也有包含这块的内容日志,详情如下:
I0721 10:38:15.326920 4692 net.cpp:125] Top shape: 256 3 227 227 (39574272)
I0721 10:38:15.326971 4692 net.cpp:125] Top shape: 256 1 1 1 (256)
I0721 10:38:15.326982 4692 net.cpp:156] data does not need backward computation.
I0721 10:38:15.327003 4692 net.cpp:74] Creating Layer conv1
I0721 10:38:15.327011 4692 net.cpp:84] conv1 <- data
I0721 10:38:15.327033 4692 net.cpp:110] conv1 -> conv1
I0721 10:38:16.721956 4692 net.cpp:125] Top shape: 256 96 55 55 (74342400)
I0721 10:38:16.722030 4692 net.cpp:151] conv1 needs backward computation.
I0721 10:38:16.722059 4692 net.cpp:74] Creating Layer relu1
I0721 10:38:16.722070 4692 net.cpp:84] relu1 <- conv1
I0721 10:38:16.722082 4692 net.cpp:98] relu1 -> conv1 (in-place)
I0721 10:38:16.722096 4692 net.cpp:125] Top shape: 256 96 55 55 (74342400)
I0721 10:38:16.722105 4692 net.cpp:151] relu1 needs backward computation.
I0721 10:38:16.722116 4692 net.cpp:74] Creating Layer pool1
I0721 10:38:16.722125 4692 net.cpp:84] pool1 <- conv1
I0721 10:38:16.722133 4692 net.cpp:110] pool1 -> pool1
I0721 10:38:16.722167 4692 net.cpp:125] Top shape: 256 96 27 27 (17915904)
I0721 10:38:16.722187 4692 net.cpp:151] pool1 needs backward computation.
I0721 10:38:16.722205 4692 net.cpp:74] Creating Layer norm1
I0721 10:38:16.722221 4692 net.cpp:84] norm1 <- pool1
I0721 10:38:16.722234 4692 net.cpp:110] norm1 -> norm1
I0721 10:38:16.722251 4692 net.cpp:125] Top shape: 256 96 27 27 (17915904)
I0721 10:38:16.722260 4692 net.cpp:151] norm1 needs backward computation.
I0721 10:38:16.722272 4692 net.cpp:74] Creating Layer conv2
I0721 10:38:16.722280 4692 net.cpp:84] conv2 <- norm1
I0721 10:38:16.722290 4692 net.cpp:110] conv2 -> conv2
I0721 10:38:16.725225 4692 net.cpp:125] Top shape: 256 256 27 27 (47775744)
I0721 10:38:16.725242 4692 net.cpp:151] conv2 needs backward computation.
I0721 10:38:16.725253 4692 net.cpp:74] Creating Layer relu2
I0721 10:38:16.725261 4692 net.cpp:84] relu2 <- conv2
I0721 10:38:16.725270 4692 net.cpp:98] relu2 -> conv2 (in-place)
I0721 10:38:16.725280 4692 net.cpp:125] Top shape: 256 256 27 27 (47775744)
I0721 10:38:16.725288 4692 net.cpp:151] relu2 needs backward computation.
I0721 10:38:16.725298 4692 net.cpp:74] Creating Layer pool2
I0721 10:38:16.725307 4692 net.cpp:84] pool2 <- conv2
I0721 10:38:16.725317 4692 net.cpp:110] pool2 -> pool2
I0721 10:38:16.725329 4692 net.cpp:125] Top shape: 256 256 13 13 (11075584)
I0721 10:38:16.725338 4692 net.cpp:151] pool2 needs backward computation.
I0721 10:38:16.725358 4692 net.cpp:74] Creating Layer norm2
I0721 10:38:16.725368 4692 net.cpp:84] norm2 <- pool2
I0721 10:38:16.725378 4692 net.cpp:110] norm2 -> norm2
I0721 10:38:16.725389 4692 net.cpp:125] Top shape: 256 256 13 13 (11075584)
I0721 10:38:16.725399 4692 net.cpp:151] norm2 needs backward computation.
I0721 10:38:16.725409 4692 net.cpp:74] Creating Layer conv3
I0721 10:38:16.725419 4692 net.cpp:84] conv3 <- norm2
I0721 10:38:16.725427 4692 net.cpp:110] conv3 -> conv3
I0721 10:38:16.735193 4692 net.cpp:125] Top shape: 256 384 13 13 (16613376)
I0721 10:38:16.735213 4692 net.cpp:151] conv3 needs backward computation.
I0721 10:38:16.735224 4692 net.cpp:74] Creating Layer relu3
I0721 10:38:16.735234 4692 net.cpp:84] relu3 <- conv3
I0721 10:38:16.735242 4692 net.cpp:98] relu3 -> conv3 (in-place)
I0721 10:38:16.735250 4692 net.cpp:125] Top shape: 256 384 13 13 (16613376)
I0721 10:38:16.735258 4692 net.cpp:151] relu3 needs backward computation.
I0721 10:38:16.735302 4692 net.cpp:74] Creating Layer conv4
I0721 10:38:16.735312 4692 net.cpp:84] conv4 <- conv3
I0721 10:38:16.735321 4692 net.cpp:110] conv4 -> conv4
I0721 10:38:16.743952 4692 net.cpp:125] Top shape: 256 384 13 13 (16613376)
I0721 10:38:16.743988 4692 net.cpp:151] conv4 needs backward computation.
I0721 10:38:16.744000 4692 net.cpp:74] Creating Layer relu4
I0721 10:38:16.744010 4692 net.cpp:84] relu4 <- conv4
I0721 10:38:16.744020 4692 net.cpp:98] relu4 -> conv4 (in-place)
I0721 10:38:16.744030 4692 net.cpp:125] Top shape: 256 384 13 13 (16613376)
I0721 10:38:16.744038 4692 net.cpp:151] relu4 needs backward computation.
I0721 10:38:16.744050 4692 net.cpp:74] Creating Layer conv5
I0721 10:38:16.744057 4692 net.cpp:84] conv5 <- conv4
I0721 10:38:16.744067 4692 net.cpp:110] conv5 -> conv5
I0721 10:38:16.748935 4692 net.cpp:125] Top shape: 256 256 13 13 (11075584)
I0721 10:38:16.748955 4692 net.cpp:151] conv5 needs backward computation.
I0721 10:38:16.748965 4692 net.cpp:74] Creating Layer relu5
I0721 10:38:16.748975 4692 net.cpp:84] relu5 <- conv5
I0721 10:38:16.748983 4692 net.cpp:98] relu5 -> conv5 (in-place)
I0721 10:38:16.748998 4692 net.cpp:125] Top shape: 256 256 13 13 (11075584)
I0721 10:38:16.749011 4692 net.cpp:151] relu5 needs backward computation.
I0721 10:38:16.749022 4692 net.cpp:74] Creating Layer pool5
I0721 10:38:16.749030 4692 net.cpp:84] pool5 <- conv5
I0721 10:38:16.749039 4692 net.cpp:110] pool5 -> pool5
I0721 10:38:16.749050 4692 net.cpp:125] Top shape: 256 256 6 6 (2359296)
I0721 10:38:16.749058 4692 net.cpp:151] pool5 needs backward computation.
I0721 10:38:16.749074 4692 net.cpp:74] Creating Layer fc6
I0721 10:38:16.749083 4692 net.cpp:84] fc6 <- pool5
I0721 10:38:16.749091 4692 net.cpp:110] fc6 -> fc6
I0721 10:38:17.160079 4692 net.cpp:125] Top shape: 256 4096 1 1 (1048576)
I0721 10:38:17.160148 4692 net.cpp:151] fc6 needs backward computation.
I0721 10:38:17.160166 4692 net.cpp:74] Creating Layer relu6
I0721 10:38:17.160177 4692 net.cpp:84] relu6 <- fc6
I0721 10:38:17.160190 4692 net.cpp:98] relu6 -> fc6 (in-place)
I0721 10:38:17.160202 4692 net.cpp:125] Top shape: 256 4096 1 1 (1048576)
I0721 10:38:17.160212 4692 net.cpp:151] relu6 needs backward computation.
I0721 10:38:17.160222 4692 net.cpp:74] Creating Layer drop6
I0721 10:38:17.160230 4692 net.cpp:84] drop6 <- fc6
I0721 10:38:17.160238 4692 net.cpp:98] drop6 -> fc6 (in-place)
I0721 10:38:17.160258 4692 net.cpp:125] Top shape: 256 4096 1 1 (1048576)
I0721 10:38:17.160265 4692 net.cpp:151] drop6 needs backward computation.
I0721 10:38:17.160277 4692 net.cpp:74] Creating Layer fc7
I0721 10:38:17.160286 4692 net.cpp:84] fc7 <- fc6
I0721 10:38:17.160295 4692 net.cpp:110] fc7 -> fc7
I0721 10:38:17.342094 4692 net.cpp:125] Top shape: 256 4096 1 1 (1048576)
I0721 10:38:17.342157 4692 net.cpp:151] fc7 needs backward computation.
I0721 10:38:17.342175 4692 net.cpp:74] Creating Layer relu7
I0721 10:38:17.342185 4692 net.cpp:84] relu7 <- fc7
I0721 10:38:17.342198 4692 net.cpp:98] relu7 -> fc7 (in-place)
I0721 10:38:17.342208 4692 net.cpp:125] Top shape: 256 4096 1 1 (1048576)
I0721 10:38:17.342217 4692 net.cpp:151] relu7 needs backward computation.
I0721 10:38:17.342228 4692 net.cpp:74] Creating Layer drop7
I0721 10:38:17.342236 4692 net.cpp:84] drop7 <- fc7
I0721 10:38:17.342245 4692 net.cpp:98] drop7 -> fc7 (in-place)
I0721 10:38:17.342254 4692 net.cpp:125] Top shape: 256 4096 1 1 (1048576)
I0721 10:38:17.342262 4692 net.cpp:151] drop7 needs backward computation.
I0721 10:38:17.342274 4692 net.cpp:74] Creating Layer fc8
I0721 10:38:17.342283 4692 net.cpp:84] fc8 <- fc7
I0721 10:38:17.342291 4692 net.cpp:110] fc8 -> fc8
I0721 10:38:17.343199 4692 net.cpp:125] Top shape: 256 22 1 1 (5632)
I0721 10:38:17.343214 4692 net.cpp:151] fc8 needs backward computation.
I0721 10:38:17.343231 4692 net.cpp:74] Creating Layer loss
I0721 10:38:17.343240 4692 net.cpp:84] loss <- fc8
I0721 10:38:17.343250 4692 net.cpp:84] loss <- label
I0721 10:38:17.343264 4692 net.cpp:151] loss needs backward computation.
I0721 10:38:17.343305 4692 net.cpp:173] Collecting Learning Rate and Weight Decay.
I0721 10:38:17.343327 4692 net.cpp:166] Network initialization done.
I0721 10:38:17.343335 4692 net.cpp:167] Memory required for Data 1073760256 参考:http://en.wikipedia.org/wiki/Convolutional_neural_network#Dropout_.22layer.22。............





 本文探讨了卷积神经网络(CNN)在图像识别领域的应用与发展历程,从LeNet到AlexNet,介绍了CNN如何通过局部连接、参数共享及池化等机制减少参数数量,以及在大数据和GPU加速的支持下如何解决过拟合问题。文章还详细解析了AlexNet的网络结构及其技术创新。
本文探讨了卷积神经网络(CNN)在图像识别领域的应用与发展历程,从LeNet到AlexNet,介绍了CNN如何通过局部连接、参数共享及池化等机制减少参数数量,以及在大数据和GPU加速的支持下如何解决过拟合问题。文章还详细解析了AlexNet的网络结构及其技术创新。




















 6479
6479

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








