目录
摘要
在本周中,我进行了关于PINN的文献阅读,文献中使用PINN来对SVE和ADE进行了预测,展现了PINN的预测准确及可行性。Fluent案例部分,本周进行的是阶梯管的流动分析,分析水在不同尺寸的圆管中的流动情况,计算求解器设置为层流,网格划分时对每个尺寸的圆管进行尺寸调整命令来划分网格。此外,对Fluent的湍流模型进行了学习研究。
Abstract
During the week, I read the literature on PINN, which used PIN to predict SVE and ADE, showing the accuracy and feasibility of PINN's predictions. In the Fluent case section, this week I did a flow analysis of stepped pipes, analyzing the flow of water in different sizes of round pipes, the calculation solver was set to laminar flow, and the size adjustment command was performed on each size of round pipe during meshing to mesh. In addition, I mainly learned about the turbulence model of Fluent .
文献阅读:1-D coupled surface flow and transport equations revisited via the physics-informed neural network approach
现有问题
1.在现实中,污染源往往是随机分布的,污染物的排放浓度也不均匀,给防治工作带来了困难。
2.溶质输运的过程是由流体的流动特性和溶质的性质决定的,因此必须采用由流体动力和浓度两个相互依赖的变量组成的模型来研究流体。
求解方程介绍
1.SVE方程
在本研究中,我们将运动波动方程(全动态SVE的简化)称为SVE。SVE是根据质量和动量平衡方程推导出来的。通常,在现实场景中,SVE中的加速项可以忽略不计,这将SVE简化为抛物方程。在这种简化的SVE形式中,忽略了侧向入流、风切变和涡动损失。一维通道的简化SVE可以表示为为:

其中Q为流(L3. T-1); x为空间维度(L); Ac为截面积(L2);t是时间维度(t)。
为了评价PINN在求解单个de Saint-Venant方程中的性能,解决了以下问题。考虑初始流量Q(x,t) = 2.5L3T-1在t = 0和x = 0时,x∈(0,1),我们通过使用正弦近似Q(x,t) = Q0 sin(πt)来调节流量来模拟大坝运行的效果,其中Q0表示过量流量。我们强制时域t∈(0,1),空间域x∈(0,1)。
Ac的计算方程如下:流量Q可利用曼宁公式进行计算,再通过截面积A-c来计算水力半径后得出SVE的数值解,详细推导可见文献中的附录A。

2.ADE方程
ADE的数学表达式为:

式中,C表示溶质在水体中的浓度(ML-3), t表示时间(t), x表示长度(L), D表示扩散系数(L2 t-1),v表示流速(LT-1),k表示一阶衰减率(t-1)。ADE的解析解详情见文献中的附录B。
ADE的准确性对于估算地表水中的污染物浓度分布至关重要。de Saint-Venant方程(SVE)描述了明渠和其他具有自由水面的浅水中的非定常流运动。它通常用于模拟地表径流中的流量。流场为求解浓度场提供了必要的参数,是精确求解ADE的关键组成部分。溶质运移过程是由流体的流动特性和溶质的性质决定的,因此研究流体动力学和污染物动力学必须采用由两个相互依赖的变量(水动力和浓度变量)组成的模型。在目前的工作中,水动力模型基于浅水方程,而溶质输运使用平流扩散方程。将SVE与ADE相结合,可以实现溶质输运的数值模拟和预测。
但求解SVE和ADE的耦合方程(SVE-ADE)仍面临一些挑战,例如适应变化和不连续的参数以及处理不同的边界条件。
SVE和ADE耦合方程面临的问题
- 由于传统数值解在空间和时间上的微分固有的离散化近似,不可避免地与不连续和数值误差联系在一起。虽然通过减小网格大小可以减少数值误差,但这会导致计算成本的增加。
- 不规则区域网格离散化的不当实施可能导致不准确的模拟结果,并阻碍污染控制方案。
- 数值方法在某些条件下可能表现出振荡或数值色散,在求解逆问题时,它们对噪声数据的适应性较差。
已经提出了各种方法来提高标准多项式有限元方法的稳定性,例如流线迎风Petrov-Galerkin (SUPG) , Galerkin最小二乘法,以及不寻常的稳定有限元法(USFEM) 其他方法,包括模型约简技术、差分进化算法和配置方法,已被用于解决地下水相关问题的逆问题,而Trefftz方法和径向基函数(RBF)方法已被用于解决不适定逆问题。
然而,这些方法需要大量的计算量,不能保证全局最优解。他们还必须依靠数值方法来迭代求解偏微分方程(PDEs)。
本研究旨在评估不同条件下PINN在求解SVE、ADE和耦合形式方面的性能,并寻求解决以下问题:
- 如何构建求解地表水不同初始条件和边界条件下ADE、SVE及耦合方程的PINN模型,准确模拟污染物运移问题?
- 如何训练神经网络来优化模型参数和结构,从而更加全面、系统地改进解?
- PINN模型是否适合求解带噪声数据的逆问题,如何提高其精度?
为了评价PINN在求解单个de Saint-Venant方程中的性能,解决了以下问题。考虑初始流量Q(x,t) = 2.5L3T-1在t = 0和x = 0时,x∈(0,1),我们通过使用正弦近似Q(x,t) = Q0 sin(πt)来调节流量来模拟大坝运行的效果,其中Q0表示过量流量。Ac的计算详见附录a。我们强制时域t∈(0,1),空间域x∈(0,1)。
由于上述条件下SVE的解析解目前无法获得,因此采用数值方法获得参考解。
研究方式
文献中通过评估了PINN在求解表面流动和溶质输运方程(ADE和SVE)中的适用性。包括三个不同的测试场景:
- 使用PINN来解决SVE(记为场景1或SC1);
- 使用PINN求解平流扩散方程(记为Scenario 2或SC2);
- PINN用于求解SVE和ADE的耦合系统(记为场景3或SC3)。
下图说明了利用PINN求解耦合方程的过程。值得注意的是,该神经网络能够同时提供流场和浓度场的结果。以下步骤列举了实现PINN解决方案的具体过程细节:

定义SVE的PINN近似残差为:

定义ADE的PINN近似残差为:

将ADE中的扩散系数(D)设为0 L2 T-1,并且耦合SVE-ADE的PINN近似残差为:

其中d(x, t)、g(x, t)和h(x, t)分别表示SVE、ADE和SVEADE的pin值。Q(x, t)和C(x, t)是DNN的输出。D (x, t), g(x, t), h(x, t)可以通过最小化均方误差作为损失函数来学习:


式中:{xi 0, Qi 0, Ci 0}为初始数据,i = 1,…,N0, N0为初始训练数据个数。{xi b, t i b, Qi b, Ci b}Nb i=1对应训练数据的边界点,其中i=1,…,Nb, Nb为边界上的训练数据个数。{xi d, ti d}Nd i=1, {xi g, ti g}Ng i=1, {ti h, xi h}Nh i=1表示d(x, t), g(x, t), h(x, t)的搭配点,其中i=1,…,Nd (Ng, Nh), Nd, Ng, Nh是搭配点的个数。
MSESC10、MSESC20和MSESC30表示初始数据的损失,而MSESC1b、MSESC2b和MSESC3b表示边界条件的损失。此外,MSEd、MSEg和MSEh在一组有限的并置点上执行SVE、ADE和SVE-ADE强加的结构。
为了评估PINN解的准确性,使用相对L2误差比较了PINN与解析解(如果适用)或数值解之间的误差,其计算公式为:

其中,向量c和向量c分别表示在均匀网格上计算的解析解或数值解和在时空域中的PINN解。
在初始条件和边界条件的基础上,在神经网络中加入物理方程作为附加约束,使训练结果满足基本物理定律,并利用自动微分(AD)和L-BFGS-B优化器分别对物理信息进行正则化和梯度优化。
不同场景下PINN的参数设置如下表所示:

在SC1中,初始条件和边界条件的数据大小设置为2000,PDE的并置点为8000。网络由10层组成,每层50个神经元,输出层1个神经元。
在SC2中,初始条件和边界条件的数据量减少到200,PDE的并置点为10,000。网络架构包括8层,每层20个神经元,输出层1个神经元。
在SC3中,所有设置与SC1相同。对于求解SVE和ADE的耦合系统,由于DNN同时逼近了放电和浓度,所以输出层的神经元数设置为2。
在优化过程中使用0.001的学习率,对于两步训练方案,使用Adam执行2000次迭代,然后使用L-BFGS-B进行优化直到收敛。这些参数设置适用于上述三种情况。
文献案例
案例一:PINN预测ADE方程的准确性
本次选用其中的瞬时释放案例进行介绍:
下图(a)显示了PINN模型预测的瞬时释放情景(Case 1)的时空解。可以观察到,随着距离上游边界的增加,浓度降低。图2(b)显示了解析解和PINN预测解之间的对数差异,其中最大对数差异小于10-2。我们发现,在河流的上游边界处,PINN溶液的差异最大,这里的浓度梯度最大。对PINN预测解的进一步评价如图2(c)-(e)所示,图2(c)-(e)显示了不同位置(即x = 0.2, 0.4和0.6 l)的解析解与PINN预测解的比较。结果表明,PINN解与解析解几乎完全吻合,相对L2误差为3.6 ×10-3,表明神经网络模型在求解瞬时释放场景的1-D ADE方面表现良好。
溶质瞬间释放到流中的平流扩散方程的解:(a)使用物理信息神经网络(PINN)方法预测的浓度C(x, t);(b)解析解与PINN预测解之间的对数差,其中CPINN为PINN解出的浓度,Cana为解析解;(c) - (e)三个位置的PINN预测解与解析解的比较,用(a)中的白色实线垂直线表示。蓝色实线代表解析解,红色虚线代表PINN预测解

案例2:PINN预测SVE方程和SVE-ADE耦合方程
本案例是将PINN应用于耦合SVE- ade所获得的结果,因为它的性能与独立SVE的解决方案相当。但为了全面理解,通过PINN获得的单机SVE解决方案已包含在附录中。使用PINN方法求解SVE的相对L2误差为7.3 × 10-3,也可以模拟流场。
用PINN方法求解流场Q(x, t)和浓度场C(x, t)以及初始条件和边界条件训练数据位置的结果分别如图6(a)和6(b)所示。图6(c)和图6(d)给出了求解不同时刻(t = 0.2、0.4、0.6和0.8 t) Q(x, t)和c (x, t)的数值方法和PINN方法的比较,结果表明,PINN方法可以准确地捕捉激波行为,而数值解由于数值离散,在最大流量和浓度附近产生了一个平坦的解。我们的研究结果表明,PINN方法在求解SVE-ADE耦合方程方面可能优于数值方法。此外,Q(x, t)和C(x, t)的相对L2误差分别为1.00 × 10-3和1.36 × 10-3,进一步证实了PINN方法的可靠性。
同时迭代求解耦合地表水方程SVE-ADE。采用迭代耦合(IC)算法,每次迭代都使用一个方程的解来更新另一个方程,反之亦然,直到获得同时满足两个方程的收敛解。虽然这个过程在计算上很昂贵,并且可能需要多次迭代才能收敛,特别是对于高度非线性问题,但PINN方法绕过了这一要求。
如下图所示的结果表明,PINN方法可以减轻数值扩散和振荡。该方法通过求解流场和浓度场,精确地模拟了激波的形状:

耦合方程的解:(a) - (b)利用物理信息神经网络(PINN)预测流量Q(x, t)和浓度C(x, t),以及初始条件和边界条件的训练数据;(c) - (d)不同时间快照下流量Q(x, t)和浓度c (x, t)的PINN预测解与数值解的比较。虚线表示数值解,实线表示预测解。
误差分析
PINN在不同初始和边界条件(Nu)和配置点(Nf)下的预测误差可见下表:

具有不同层数和神经元的PINN的预测误差可见下表:

在表中可以看出,当使用PINN求解ADE时,每种情况下相对L2误差的浮动范围都很小。这些结果表明,随机种子的设置对模型结果的影响很小。虽然种子选择会影响机器学习模型的结果,但PINN算法的基础物理约束最小化了随机权重初始化对最终输出的影响,确保了结果的鲁棒性和可重复性。
结论
研究结果表明,由于神经网络能够很好地拟合函数并容纳pde的物理信息,PINN是求解地表水方程的一种很有前途的方法。PINN方法在求解SVE和耦合SVE- ade方程时准确地捕捉了激波的形状。我们进一步研究了初始和边界条件(Nu)、并置点(Nf)、网络层和神经元的数量对PINN解的准确性的影响。所以PINN方法的准确性与Nu、Nf、网络层和神经元的数量呈正相关。
此外,PINN对噪声数据有很高的容忍度。适当增加Nu的个数可以提高PINN算法对含噪声数据逆问题的仿真精度。这些结果说明了PINN方法在解决多物理场问题方面的潜力。这项工作有助于证明PINN在模拟地表水污染物迁移中的适用性,可以为该领域的未来研究提供参考。
在更复杂或更现实的条件下,如复杂的几何和边界条件、非线性和异质性、噪声和不确定性、计算资源等,PINN的应用也面临着一些可预见的挑战。在现阶段,使用PINN开发一般类型的PDE求解器仍处于起步阶段,PINN的功能仍不能完全取代传统方法。在不同的初始条件或边界条件下,以及在不同的流动条件下,PINN求解SVE-ADE的传递能力还有待探索。虽然这些挑战肯定不是微不足道的,但我们相信,PINN方法有潜力解决这些问题。神经网络固有的灵活性和能力可以用来处理复杂的几何形状、非线性和异构性,并且可以应用各种技术使PINN对噪声和不确定性具有鲁棒性。
Fluent案例:阶梯管的流动分析
本周的案例为:分析水在不同尺寸的圆管中的流动情况,计算求解器设置为层流,网格划分时对每个尺寸的圆管进行尺寸调整命令来划分网格。
几何建模部分
本次建模如下图所示,从小到大的圆管管壁长度为40,50,70,100mm,管道半径从小到大为:20,30,40,50mm。通过绕x轴旋转生成模型:

网格划分部分:
先通过自动划分,进行几何质量判断,若网格划分不出错,则建模封闭性足够,以下为四面体网格划分结果:

而后对每个圆柱体进行尺寸调整,采用分区数量命令,分为100个单位网格。都采用硬性划分,网格划分结果如下图所示:

再对四个面进行面网格划分命令,分区数量采用55,划分如下:

总网格数量见下图:

对入口、出口、流体区域进行命名,将管道由大到小命名为S1、S2、S3、S4,后转入求解器设置。
求解器设置
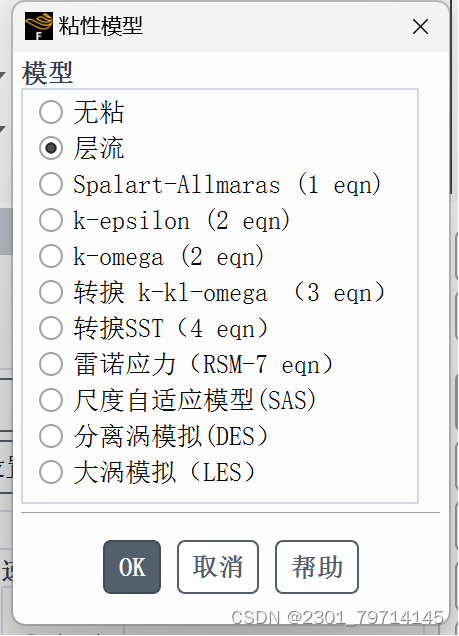
求解模式设置为层流,流体材料为水,固体材料设置为钢铁:
水的材料条件如下:

钢铁的材料条件如下:

更改流体材料为水后,设置初始条件,进口速度设置为0.001m/s,其余保持默认:

采用SIMPLE方法求解,梯度采用二阶高斯区域条件来进行求解:

设置残差为0.000001:

对求解做初始化,计算区域为所有区域:
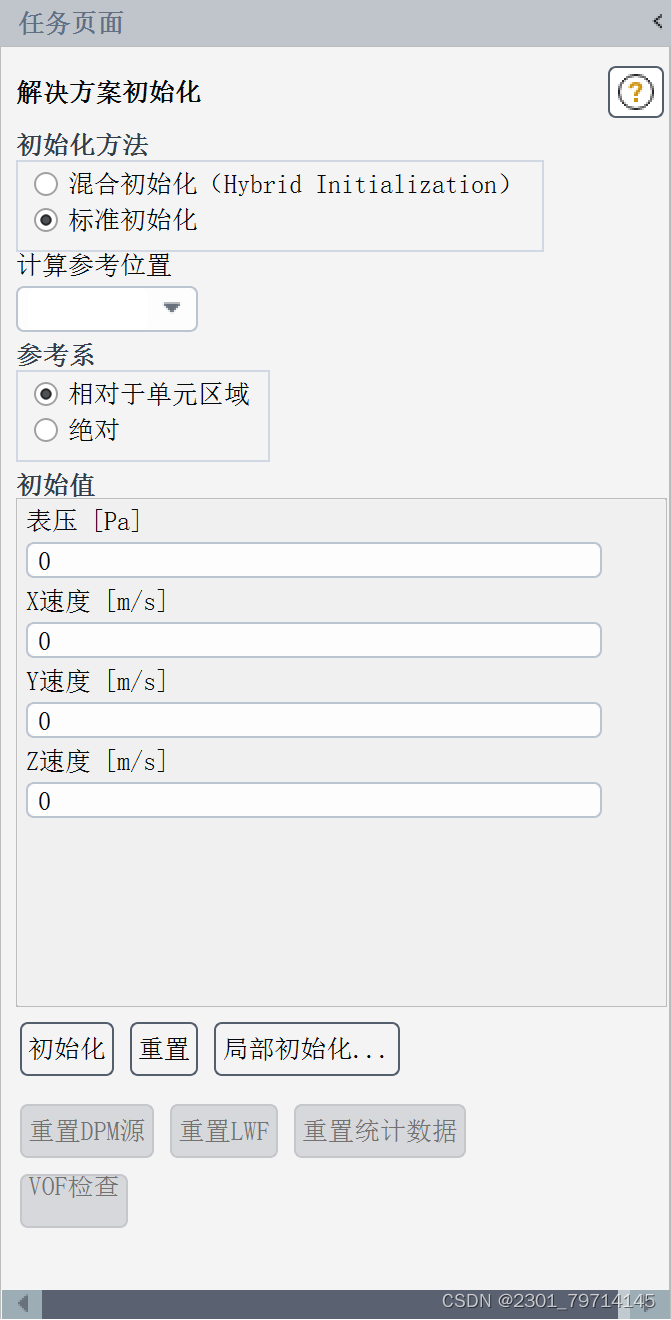
迭代次数设置为1000次,结果如下:

各流通面压力云图:

各流通面速度云图:

速度流线图:

湍流模型学习:
雷诺模型部分:











大涡模型部分:

总结
在本周通过查阅文献和资料,了解到PINN在预测方面的领先性和准确性,对其基本原理和函数写法有了基本的理解。在关于湍流模型的学习中,通过学习推导各方程,学会了其大致的框架和使用情况。在下次的学习将会对PINN的深度学习部分进行补充学习,已便更好了解其原理和逼近形式。




















 994
994











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








