PX4固定翼控制器详解(三)——TECS高度、速度控制器

在前两期的文章中，我们详细介绍了姿态控制器。通过回顾之前关于导航、制导与控制的文章，我们可以看到无人机的整体控制框架中，姿态控制器的作用是将期望姿态指令转化为作动器的输出。接下来的挑战是如何根据期望的位置指令，为姿态控制器生成相应的期望姿态指令。

本期先从高度控制器讲起，着重介绍PX4中高度、速度控制的TECS控制器。

简易高度控制器

设计高度控制器时，如果你参考相关书籍，大部分给出的控制框图类似是这样的。
（该图出自《飞行控制系统（第二版）》第245页，图5-49典型的高度稳定和控制系统原理图。）

图1 典型高度稳定和控制系统原理图

如果第一次看会感觉非常莫名奇妙，为什么套了这么多环？最后输出的控制量是${\delta }_e$升降舵偏？
根据控制框图，不难写出输入舵回路的期望舵偏控制率为：
$$\Delta {\delta }_{\mathrm{e}}=K_z^{\theta }\Delta \theta +K_z^{\dot{\theta }}\Delta \dot{\theta }+K_z^h(\Delta h-\Delta h_{\mathrm{g}})+K_z^{\dot{h}}\Delta \dot{h}$$
其本质是基于控制俯仰角，来实现高度的变化控制。除此之外，还引入了高度差的一节微分$\Delta \dot{h}$，用以改善高度控制的阻尼特性。

基于我们前期已经设计好了姿态控制器，能否根据高度差算一个期望的俯仰角，将期望俯仰角${\theta }_{sp}$作为姿态控制器的输入呢？显然是可行的，具体控制框图如下图2所示：

图2 基于姿态控制器的高度控制

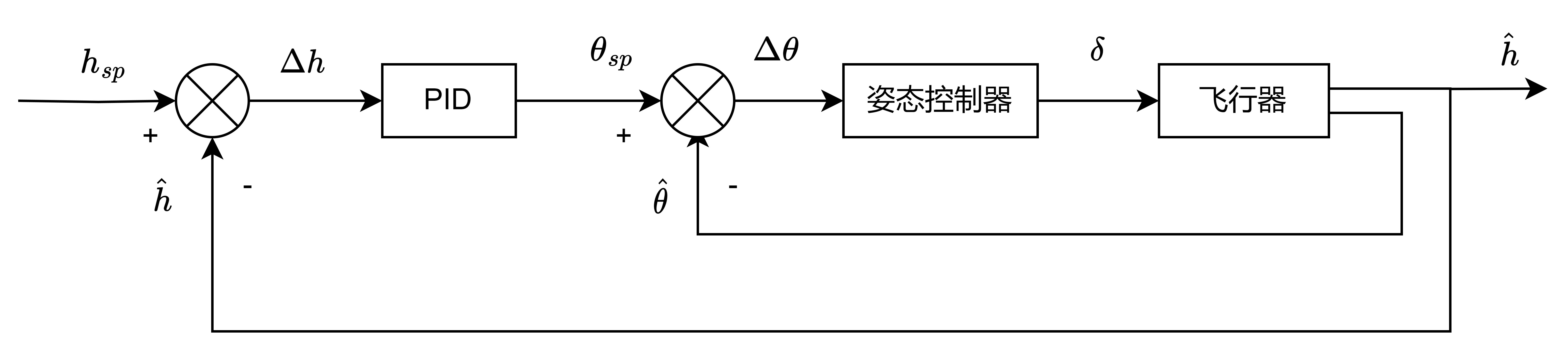
可以看出此控制方法充分利用到了我们前期已经设计好的姿态控制器。我们所需要做的就是根据高度差，计算一个期望的俯仰角${\theta }_{sp}$，交由姿态控制器输出最终舵偏角${\delta }_e$。

实际上该方法，与图1给出的高度控制方法并无本质区别，均引入了高度误差作为控制量。高度误差做PID控制和高度误差乘以$K_h+K_{\dot{h}}s$做反馈控制，这两种设计思路本质是类似的。再看图1中的两层内环的反馈控制，说白了也是和姿态控制器的双回路PID控制器类似。

但如果你直接看图1给出的高度控制器，大部分人可能无法直接看懂。

我们现在知道了高度控制方法，如果同时需要控制飞行速度，这时候应该怎么办呢？

高度控制回路和速度控制回路两者是相互耦合的：

• 当尝试拉升降舵爬升高度时，飞行速度会下降；
• 当推油门加速时，高度会升高；收油门减速时，高度会下降。

从解耦控制思路出发，如果熟悉状态空间，有很多方法可以解决这个问题，但前提是需要有比较精确完整的动力学模型。而针对大部分小型固定翼无人机而言，要想完整获取动力学模块，使用CFD或风动实验对整个代价是较高的。这里我们不考虑根据完整的被控对象模型去做解耦控制，采用一种基于能量法的高度-速度控制——总能量控制系统（TECS——Total Energy Control System）。

TECS 总能量控制系统

总能量原理

总能量控制系统最早(TECS)是在1979年到1985年期间Boeing公司为NASA工作时提出的。该系统基本思想是通过计算飞行过程的总能量（动能+势能），使用油门和升降舵来分配总能量，来实现速度和高度的解耦控制。

飞机在垂直平面内飞行，其质点运动方程可以写为：
$$\{\begin{array}{l}dx/dt=V_T\cos \gamma +V_w\\ dh/dt=V_T\sin \gamma \\ d{V}_T/dt=(T-D)/m-g\sin \gamma \end{array}$$
式中，$x$为飞行距离，$V_T$为空速，$m$为飞机质量，$T$为推力，$D$为阻力，$h$为高度，$\gamma$为垂直平面内纵向俯仰航迹倾角，$V_w$为风速。

飞机的总能量 E T E_T ET​</