技不如人, 甘拜下风. —刀斯林
🏰代码及环境配置：请参考0.2 环境配置和代码运行 | 动手学运动规划!
1.1, 1.2节我们介绍了车辆运动学, 讲解了通过定义状态变量, 控制变量, 状态转移的方式, 来简化车辆的运动. 在运动规划算法中, 直接构造车辆运动学模型, 或者说基于最优控制的轨迹规划. 虽然相对真实和精确, 但是也有它的缺点:
- 模型的约束一般都是非线性约束, 在优化问题中, 要么将其线性化(丧失精度), 要么构造非线性约束(计算量大)
- 模型的状态变量, 控制变量一般较多, 相应的需要更多的计算量
因此我们也常用各种形式的曲线来表达车辆轨迹, 与车辆运动模型直接约束控制变量不同的是, 可以通过约束曲线变量来间接的实现相应约束. 比如在车辆运动模型中, 我们通过约束前轮偏角 δ \delta δ的范围来约束车辆的最小转弯半价. 而在曲线中, 直接约束曲线的曲率 k k k就能达到类似的效果.
本章将会对运动规划算法中常见的曲线形式进行介绍. 首先, 我们从最基础的基于5次多项式的参数方程开始.
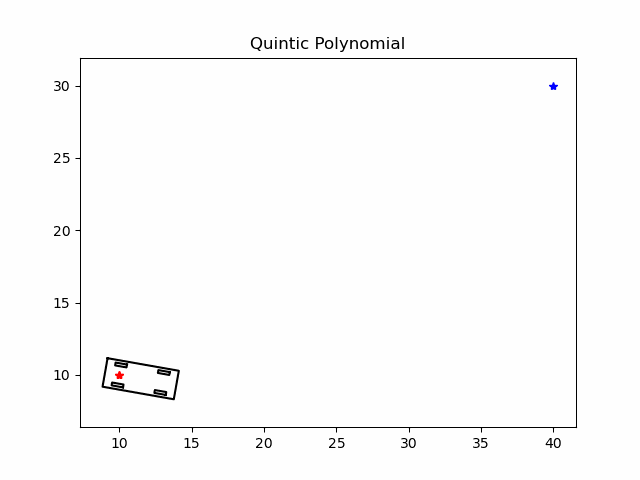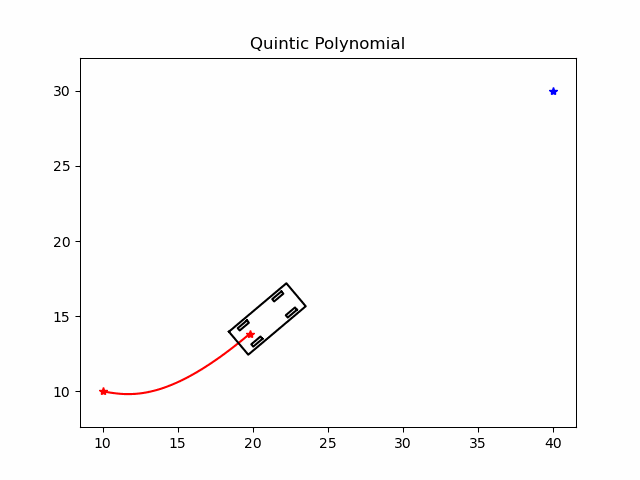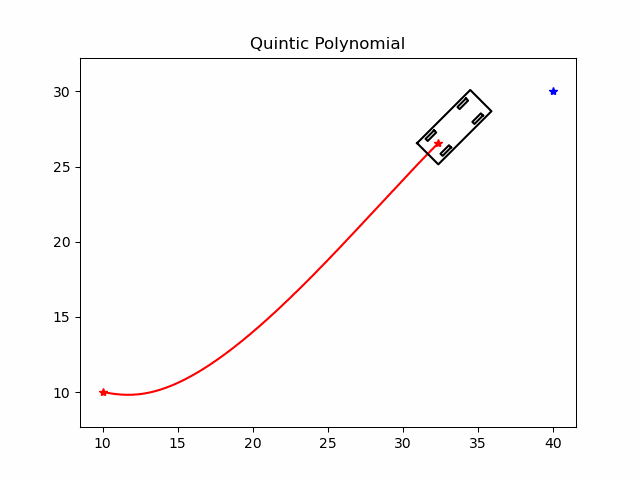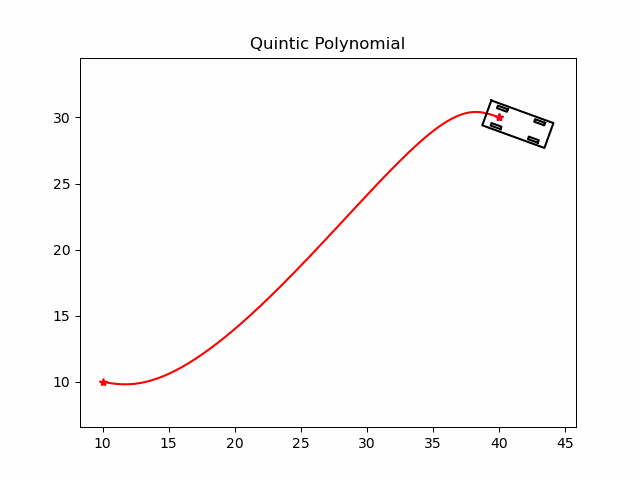
2.1.1 基于5次多项式的参数方程定义
假设车辆是一个质点, x和y是质点的坐标, t是时间. x和y分别用关于t的5次多项式参数方程表达:
x ( t ) = a 0 + a 1 t + a 2 t 2 + a 3 t 3 + a 4 t 4 + a 5 t 5 y ( t ) = b 0 + b 1 t + b 2 t 2 + b 3 t 3 + b 4 t 4 + b 5 t 5 \begin{align*} x(t) &=a_0+a_1 t+a_2 t^2+a_3 t^3+a_4 t^4+a_5 t^5 \\ y(t) &=b_0+b_1 t+b_2 t^2+b_3 t^3+b_4 t^4+b_5 t^5 \end{align*} x(t)y(t)=a0+a1t+a2t2+a3t3+a4t4+a5t5=b0+b1t+b2t2+b3t3+b4t4+b5t5
a 0 , a 1 . a 2 , a 3 , a 4 , a 5 a_0, a_1. a_2, a_3, a_4, a_5 a0,a
最低0.47元/天 解锁文章
扫一扫
870
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
