卡尔曼滤波器推导如下:
由
k
−
1
k-1
k−1到
k
k
k时刻,系统状态方程
x
k
=
A
x
k
−
1
+
B
u
k
+
C
w
k
x_k=Ax_{k-1}+Bu_k+Cw_k
xk=Axk−1+Buk+Cwk
系统观测方程
y
k
=
H
x
k
+
v
k
y_k=Hx_k+v_k
yk=Hxk+vk
其中,
x
k
x_k
xk为真实值;
A
A
A为状态转移矩阵;
u
k
u_k
uk为系统输入;
B
B
B为输入增益矩阵;
y
k
y_k
yk为测量值;
H
H
H为观测矩阵;
w
k
∼
N
(
0
,
Q
)
w_k \sim N \left( 0,Q \right)
wk∼N(0,Q)为过程高斯噪声,
Q
Q
Q为其协方差阵;
C
C
C为过程噪声增益矩阵;
v
k
∼
N
(
0
,
R
)
v_k\sim N\left( 0,R \right)
vk∼N(0,R)为测量高斯噪声,
R
R
R为其协方差阵;
w
k
w_k
wk和
v
k
v_k
vk不相关。
卡尔曼滤波器(预测+修正):
x
^
k
′
=
A
x
^
k
−
1
+
B
u
k
x
^
k
=
x
^
k
′
+
K
k
(
y
k
−
H
x
^
k
′
)
\hat{x}_k'=A\hat{x}_{k-1}+Bu_k \\ \hat{x}_k=\hat{x}_k'+K_k\left( y_k-H\hat{x}_k' \right)
x^k′=Ax^k−1+Bukx^k=x^k′+Kk(yk−Hx^k′)
其中,
x
^
k
\hat{x}_k
x^k为卡尔曼估计值(后验);
x
^
k
′
\hat{x}_k'
x^k′为预测值(先验);
K
k
K_k
Kk为卡尔曼增益。
希望设计出 K k K_k Kk使得卡尔曼估计值接 x ^ k \hat{x}_k x^k近于系统输出的真实值 x k x_k xk 。
从协方差矩阵(对称矩阵)开始,真实值与预测值之间的误差为
e
k
′
=
x
k
−
x
^
k
′
e_k'=x_k-\hat{x}_k'
ek′=xk−x^k′
预测误差协方差矩阵为
P
k
′
=
E
[
e
k
′
e
k
′
T
]
=
E
[
(
x
k
−
x
^
k
′
)
(
x
k
−
x
^
k
′
)
T
]
P_k'=E\left[ e_k'e_k'^T \right] =E\left[ \left( x_k-\hat{x}_k' \right) \left( x_k-\hat{x}_k' \right) ^T \right]
Pk′=E[ek′ek′T]=E[(xk−x^k′)(xk−x^k′)T]
真实值与估计值之间的误差为
e
k
=
x
k
−
x
^
k
=
x
k
−
(
x
^
k
′
+
K
k
(
H
x
k
+
v
k
−
H
x
^
k
′
)
)
=
(
I
−
K
k
H
)
(
x
k
−
x
^
k
′
)
−
K
k
v
k
\begin{aligned} e_k&=x_k-\hat{x}_k=x_k-\left( \hat{x}_k'+K_k\left( Hx_k+v_k-H\hat{x}_k' \right) \right) \\ &=\left( I-K_kH \right) \left( x_k-\hat{x}_k' \right) -K_kv_k \end{aligned}
ek=xk−x^k=xk−(x^k′+Kk(Hxk+vk−Hx^k′))=(I−KkH)(xk−x^k′)−Kkvk
卡尔曼估计误差协方差矩阵为
P
k
=
E
[
e
k
e
k
T
]
=
E
[
[
(
I
−
K
k
H
)
(
x
k
−
x
^
k
′
)
−
K
k
v
k
]
[
(
I
−
K
k
H
)
(
x
k
−
x
^
k
′
)
−
K
k
v
k
]
T
]
=
(
I
−
K
k
H
)
E
[
(
x
k
−
x
^
k
′
)
(
x
k
−
x
^
k
′
)
T
]
(
I
−
K
k
H
)
T
+
K
k
E
[
v
k
v
k
T
]
K
T
=
(
I
−
K
k
H
)
P
k
′
(
I
−
K
k
H
)
T
+
K
k
R
K
k
T
\begin{aligned} P_k&=E\left[ e_ke_k^T \right] \\ &=E\left[ \left[ \left( I-K_kH \right) \left( x_k-\hat{x}_k' \right) -K_kv_k \right] \left[ \left( I-K_kH \right) \left( x_k-\hat{x}_k' \right) -K_kv_k \right] ^T \right] \\ &=\left( I-K_kH \right) E\left[ \left( x_k-\hat{x}_k' \right) \left( x_k-\hat{x}_k' \right) ^T \right] \left( I-K_kH \right) ^T+K_kE\left[ v_kv_k^T \right] K^T \\ &=\left( I-K_kH \right) P_k'\left( I-K_kH \right) ^T+K_kRK_k^T \end{aligned}
Pk=E[ekekT]=E[[(I−KkH)(xk−x^k′)−Kkvk][(I−KkH)(xk−x^k′)−Kkvk]T]=(I−KkH)E[(xk−x^k′)(xk−x^k′)T](I−KkH)T+KkE[vkvkT]KT=(I−KkH)Pk′(I−KkH)T+KkRKkT
卡尔曼滤波本质是最小均方差估计,而均方差是
P
k
P_k
Pk的迹,将上式展开并求迹,有
t
r
(
P
k
)
=
t
r
(
P
k
′
)
−
2
t
r
(
K
k
H
P
k
′
)
+
t
r
(
K
k
(
H
P
k
′
H
T
+
R
)
K
k
T
)
tr\left( P_k \right) =tr\left( P_k' \right) -2tr\left( K_kHP_k' \right) +tr\left( K_k\left( HP_k'H^T+R \right) K_k^T \right)
tr(Pk)=tr(Pk′)−2tr(KkHPk′)+tr(Kk(HPk′HT+R)KkT)
最优估计的
K
k
K_k
Kk使均方差最小,所以上式对
K
k
K_k
Kk求导,有
∂
t
r
(
P
k
)
∂
K
k
=
−
∂
t
r
(
2
K
k
H
P
k
′
)
∂
K
k
+
∂
t
r
(
K
k
(
H
P
k
′
H
T
+
R
)
K
k
T
)
∂
K
k
=
−
2
(
H
P
k
′
)
T
+
2
K
k
(
H
P
k
′
H
T
+
R
)
\begin{aligned} \frac{\partial tr\left( P_k \right)}{\partial K_k}&=-\frac{\partial tr\left( 2K_kHP_k' \right)}{\partial K_k}+\frac{\partial tr\left( K_k\left( HP_k'H^T+R \right) K_k^T \right)}{\partial K_k} \\ &=-2\left( HP_k' \right) ^T+2K_k\left( HP_k'H^T+R \right) \end{aligned}
∂Kk∂tr(Pk)=−∂Kk∂tr(2KkHPk′)+∂Kk∂tr(Kk(HPk′HT+R)KkT)=−2(HPk′)T+2Kk(HPk′HT+R)
令上式等于
0
0
0,得到
K
k
=
P
k
′
H
T
(
H
P
k
′
H
T
+
R
)
−
1
K_k=P_k'H^T\left( HP_k'H^T+R \right) ^{-1}
Kk=Pk′HT(HPk′HT+R)−1
其中
P
k
′
=
E
[
(
x
k
−
x
^
k
′
)
(
x
k
−
x
^
k
′
)
T
]
=
E
[
(
A
x
k
−
1
+
B
u
k
+
C
w
k
−
A
x
^
k
−
1
−
B
u
k
)
(
A
x
k
−
1
+
B
u
k
+
C
w
k
−
A
x
^
k
−
1
−
B
u
k
)
T
]
=
E
[
(
A
(
x
k
−
1
−
x
^
k
−
1
)
+
C
w
k
)
(
A
(
x
k
−
1
−
x
^
k
−
1
)
+
C
w
k
)
T
]
=
E
[
(
A
e
k
−
1
)
(
A
e
k
−
1
)
T
]
+
E
[
C
w
k
(
C
w
k
)
T
]
=
A
P
k
−
1
A
T
+
C
Q
C
T
\begin{aligned} P_k'&=E\left[ \left( x_k-\hat{x}_k' \right) \left( x_k-\hat{x}_k' \right) ^T \right] \\ &=E\left[ \left( Ax_{k-1}+Bu_k+Cw_k-A\hat{x}_{k-1}-Bu_k \right) \left( Ax_{k-1}+Bu_k+Cw_k-A\hat{x}_{k-1}-Bu_k \right) ^T \right] \\ &=E\left[ \left( A\left( x_{k-1}-\hat{x}_{k-1} \right) +Cw_k \right) \left( A\left( x_{k-1}-\hat{x}_{k-1} \right) +Cw_k \right) ^T \right] \\ &=E\left[ \left( Ae_{k-1} \right) \left( Ae_{k-1} \right) ^T \right] +E\left[ Cw_k\left( Cw_k \right) ^T \right] \\ &=AP_{k-1}A^T+CQC^T \end{aligned}
Pk′=E[(xk−x^k′)(xk−x^k′)T]=E[(Axk−1+Buk+Cwk−Ax^k−1−Buk)(Axk−1+Buk+Cwk−Ax^k−1−Buk)T]=E[(A(xk−1−x^k−1)+Cwk)(A(xk−1−x^k−1)+Cwk)T]=E[(Aek−1)(Aek−1)T]+E[Cwk(Cwk)T]=APk−1AT+CQCT
此时
P
k
=
P
k
′
−
K
k
H
P
k
′
−
P
k
′
H
T
K
k
T
+
K
k
(
H
P
k
′
H
T
+
R
)
K
k
T
=
P
k
′
−
K
k
H
P
k
′
−
P
k
′
H
T
K
k
T
+
P
k
′
H
T
(
H
P
k
′
H
T
+
R
)
−
1
(
H
P
k
′
H
T
+
R
)
K
k
T
=
P
k
′
−
K
k
H
P
k
′
=
(
I
−
K
k
H
)
P
k
′
\begin{aligned} P_k&=P_k'-K_kHP_k'-P_k'H^TK_k^T+K_k\left( HP_k'H^T+R \right) K_k^T \\ &=P_k'-K_kHP_k'-P_k'H^TK_k^T+P_k'H^T\left( HP_k'H^T+R \right) ^{-1}\left( HP_k'H^T+R \right) K_k^T \\ &=P_k'-K_kHP_k' \\ &=\left( I-K_kH \right) P_k' \end{aligned}
Pk=Pk′−KkHPk′−Pk′HTKkT+Kk(HPk′HT+R)KkT=Pk′−KkHPk′−Pk′HTKkT+Pk′HT(HPk′HT+R)−1(HPk′HT+R)KkT=Pk′−KkHPk′=(I−KkH)Pk′
总结如下:
模型:
x
k
=
A
x
k
−
1
+
B
u
k
+
C
w
k
x_k=Ax_{k-1}+Bu_k+Cw_k
xk=Axk−1+Buk+Cwk
y k = H x k + v k y_k=Hx_k+v_k yk=Hxk+vk
初始化:
x
^
0
\hat{x}_0
x^0
P 0 = E ( e 0 e 0 T ) = E [ ( x 0 − x ^ 0 ) ( x 0 − x ^ 0 ) T ] P_0=E\left( e_0e_0^T \right) =E\left[ \left( x_0-\hat{x}_0 \right) \left( x_0-\hat{x}_0 \right) ^T \right] P0=E(e0e0T)=E[(x0−x^0)(x0−x^0)T]
增益:
K
k
=
P
k
′
H
T
(
H
P
k
′
H
T
+
R
)
−
1
K_k=P_k'H^T\left( HP_k'H^T+R \right) ^{-1}
Kk=Pk′HT(HPk′HT+R)−1
更新:
x
^
k
=
x
^
k
′
+
K
k
(
y
k
−
H
x
^
k
′
)
\hat{x}_k=\hat{x}_k'+K_k\left( y_k-H\hat{x}_k' \right)
x^k=x^k′+Kk(yk−Hx^k′)
P k = ( I − K k H ) P k ′ P_k=\left( I-K_kH \right) P_k' Pk=(I−KkH)Pk′
预测:
x
^
k
′
=
A
x
^
k
−
1
+
B
u
k
\hat{x}_k'=A\hat{x}_{k-1}+Bu_k
x^k′=Ax^k−1+Buk
P k ′ = A P k − 1 A T + C Q C T P_k'=AP_{k-1}A^T+CQC^T Pk′=APk−1AT+CQCT
因为
P
k
P_k
Pk对角线元素是误差的方差,并且误差都服从正态分布,由数理统计的知识可知,当模拟时间
足够长,每个状态的估计误差数据各自约有99.74%会落入对应的
[
−
3
σ
,
3
σ
]
[-3\sigma,3\sigma]
[−3σ,3σ]区间,换句话说,每个状态的真值约有
99.74
%
99.74\%
99.74%出现在区间
[
x
^
k
−
3
σ
,
x
^
k
+
3
σ
]
[\hat{x}_k-3\sigma,\hat{x}_k+3\sigma]
[x^k−3σ,x^k+3σ]内。
当
B
=
O
B=O
B=O时,最优估计
x
(
k
+
1
)
x(k+1)
x(k+1)和观测矢量
y
(
1
)
,
y
(
2
)
,
⋯
,
y
(
k
+
1
)
y(1),y(2),\cdots,y(k+1)
y(1),y(2),⋯,y(k+1)之间的递归关系如下:
x
(
k
+
1
)
=
A
x
(
k
)
+
K
(
k
+
1
)
[
y
(
k
+
1
)
−
H
A
x
(
k
)
]
=
K
(
k
+
1
)
y
(
k
+
1
)
+
[
I
−
K
(
k
+
1
)
H
]
A
x
(
k
)
=
K
(
k
+
1
)
y
(
k
+
1
)
+
[
I
−
K
(
k
+
1
)
H
]
A
[
K
(
k
)
y
(
k
)
+
[
I
−
K
(
k
)
H
]
A
x
(
k
−
1
)
]
=
K
(
k
+
1
)
y
(
k
+
1
)
+
[
I
−
K
(
k
+
1
)
H
]
A
K
(
k
)
y
(
k
)
+
[
I
−
K
(
k
+
1
)
H
]
A
[
I
−
K
(
k
)
H
]
A
x
(
k
−
1
)
=
K
(
k
+
1
)
y
(
k
+
1
)
+
∑
j
=
0
k
−
1
{
[
∏
i
=
k
k
−
j
[
[
I
−
K
(
i
+
1
)
H
]
A
]
]
K
(
k
−
j
)
y
(
k
−
j
)
}
+
[
∏
i
=
k
0
[
[
I
−
K
(
i
+
1
)
H
]
A
]
]
x
(
0
)
\begin{aligned} x\left( k+1 \right) &=Ax\left( k \right) +K\left( k+1 \right) \left[ y\left( k+1 \right) -HAx\left( k \right) \right] \\ &=K\left( k+1 \right) y\left( k+1 \right) +\left[ I-K\left( k+1 \right) H \right] Ax\left( k \right) \\ &=K\left( k+1 \right) y\left( k+1 \right) + \left[ I-K\left( k+1 \right) H \right] A\left[ K\left( k \right) y\left( k \right) +\left[ I-K\left( k \right) H \right] Ax\left( k-1 \right) \right] \\ &=K\left( k+1 \right) y\left( k+1 \right) + \left[ I-K\left( k+1 \right) H \right] AK\left( k \right) y\left( k \right) + \left[ I-K\left( k+1 \right) H \right] A\left[ I-K\left( k \right) H \right] Ax\left( k-1 \right) \\ &=K\left( k+1 \right) y\left( k+1 \right) + \sum_{j=0}^{k-1}{\left\{ \left[ \prod_{i=k}^{k-j}{\left[ \left[ I-K\left( i+1 \right) H \right] A \right]} \right] K\left( k-j \right) y\left( k-j \right) \right\} +} \left[ \prod_{i=k}^0{\left[ \left[ I-K\left( i+1 \right) H \right] A \right]} \right] x\left( 0 \right) \end{aligned}
x(k+1)=Ax(k)+K(k+1)[y(k+1)−HAx(k)]=K(k+1)y(k+1)+[I−K(k+1)H]Ax(k)=K(k+1)y(k+1)+[I−K(k+1)H]A[K(k)y(k)+[I−K(k)H]Ax(k−1)]=K(k+1)y(k+1)+[I−K(k+1)H]AK(k)y(k)+[I−K(k+1)H]A[I−K(k)H]Ax(k−1)=K(k+1)y(k+1)+j=0∑k−1{[i=k∏k−j[[I−K(i+1)H]A]]K(k−j)y(k−j)}+[i=k∏0[[I−K(i+1)H]A]]x(0)
仿真:
{
x
1
(
k
+
1
)
=
x
1
(
k
)
+
x
2
(
k
)
+
w
(
k
)
x
2
(
k
+
1
)
=
x
2
(
k
)
+
w
(
k
)
y
1
(
k
+
1
)
=
x
1
(
k
+
1
)
+
v
1
(
k
+
1
)
y
2
(
k
+
1
)
=
x
2
(
k
+
1
)
+
v
2
(
k
+
1
)
k
=
0
,
1
,
⋯
⟺
{
A
=
[
1
1
0
1
]
B
=
O
C
=
[
1
1
]
H
=
[
1
0
0
1
]
E
[
w
2
]
=
1
,
E
[
v
v
T
]
=
[
1
0
0
2
]
,
E
[
w
v
T
]
=
[
0
0
0
0
]
\begin{cases} x_{1}(k+1)=x_{1}(k)+x_{2}(k)+w(k) \\ x_{2}(k+1)=x_{2}(k)+w(k)\\ y_{1}(k+1)=x_{1}(k+1)+v_{1}(k+1) \\ y_{2}(k+1)=x_{2}(k+1)+v_{2}(k+1) \\ k=0,1,\cdots \end{cases} \Longleftrightarrow \begin{cases} A=\begin{bmatrix} 1 & 1 \\ 0 & 1 \end{bmatrix} \\ B=O \\ C=\begin{bmatrix} 1 \\ 1 \end{bmatrix} \\ H=\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \end{cases}\\ E[w^{2}]=1, E[vv^{T}]=\begin{bmatrix} 1 & 0 \\ 0 & 2 \end{bmatrix}, E[wv^{T}]=\begin{bmatrix} 0 & 0 \\ 0 & 0 \end{bmatrix}
⎩
⎨
⎧x1(k+1)=x1(k)+x2(k)+w(k)x2(k+1)=x2(k)+w(k)y1(k+1)=x1(k+1)+v1(k+1)y2(k+1)=x2(k+1)+v2(k+1)k=0,1,⋯⟺⎩
⎨
⎧A=[1011]B=OC=[11]H=[1001]E[w2]=1,E[vvT]=[1002],E[wvT]=[0000]
clear;clc;close all;
N=11;% 采样点数
n=2;% 本系统2维
%% 状态和测量值初始化
X=zeros(n,N);%各时刻真实值,初始值为0
X_kf=zeros(n,N);% 估计值(Kalman滤波处理的状态)
Y=zeros(2,N); %测量值
K=zeros(n,2,N);
I=eye(n);
%% 噪声
Q=1;%W(k)的方差
R1=1;%V1(k)的方差
R2=2;%V2(k)的方差
R=[R1 0;0 R2];
rng(4);%确定随机种子,防止每次W和V不同
W=sqrt(Q)*randn(1,N);
V1=sqrt(R1)*randn(1,N);
V2=sqrt(R2)*randn(1,N);
V=[V1;V2];
%% 赋初值
X(:,1)=[0;0];%系统初值
P(:,:,1)=I;%初始值的协方差
sigma_x1_fang(1)=P(1,1,1);
sigma_x2_fang(1)=P(2,2,1);
X_kf(:,1)=[0.5;0.2];%滤波器的初始估计状态,不知道,任意
%% 系统矩阵
A=[1 1;0 1];
B=[0;0];
u_k=0;
C=[1;1];
H=[1 0;0 1];
%% 模拟测量过程,并滤波
for k=2:N
X(:,k)=A*X(:,k-1)+B*u_k+C*W(k-1);
Y(:,k)=H*X(:,k)+V(:,k);
X_pre=A*X_kf(:,k-1)+B*u_k;
P_pre=A*P(:,:,k-1)*A'+C*Q*C';
K(:,:,k)=P_pre*H'/(H*P_pre*H'+R);
P(:,:,k)=(I-K(:,:,k)*H)*P_pre;
X_kf(:,k)=X_pre+K(:,:,k)*(Y(:,k)-H*X_pre);
sigma_x1_fang(k)=P(1,1,k);
sigma_x2_fang(k)=P(2,2,k);
end
%% 误差计算
Err_Kalman_x1=X(1,:)-X_kf(1,:);
Err_Kalman_x2=X(2,:)-X_kf(2,:);
%% 绘图
t=0:N-1;
figure('Name','Kalman滤波仿真')
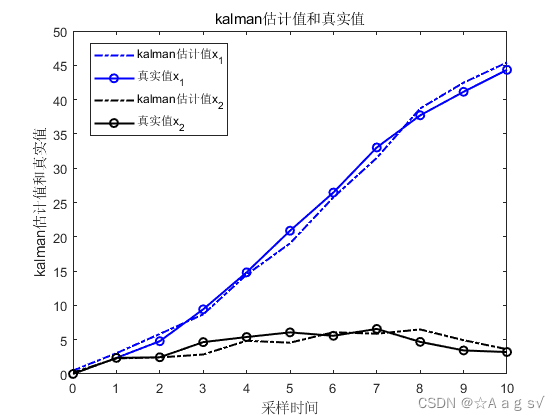
plot(t,X_kf(1,:),'-.b','LineWidth',1.5);hold on
plot(t,X(1,:),'-ob','LineWidth',1.5);hold on
plot(t,X_kf(2,:),'-.k','LineWidth',1.5);hold on
plot(t,X(2,:),'-ok','LineWidth',1.5);
legend('kalman估计值x_1','真实值x_1','kalman估计值x_2','真实值x_2');
xlabel('采样时间');
ylabel('kalman估计值和真实值');
title('kalman估计值和真实值');
figure('Name','误差分析')
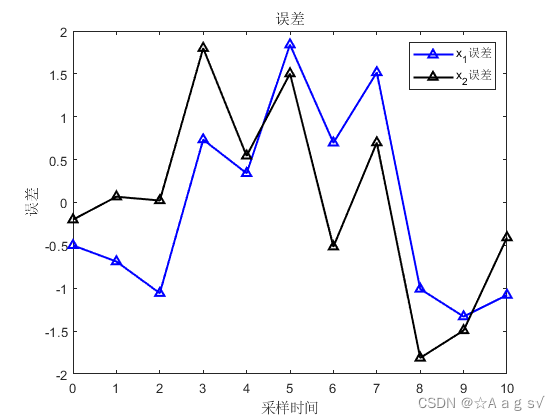
plot(t,Err_Kalman_x1,'-^b','LineWidth',1.5);
hold on
plot(t,Err_Kalman_x2,'-^k','LineWidth',1.5);
legend('x_1误差','x_2误差');
xlabel('采样时间');
ylabel('误差');
title('误差');
figure('Name','误差方差分析')
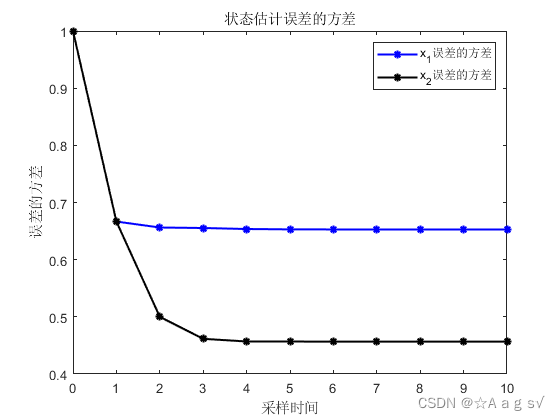
plot(t,sigma_x1_fang,'-*b','LineWidth',1.5);
hold on
plot(t,sigma_x2_fang,'-*k','LineWidth',1.5);
legend('x_1误差的方差','x_2误差的方差');
xlabel('采样时间');
ylabel('误差的方差');
title('状态估计误差的方差');
figure('Name','误差图')
sigma_x1=sigma_x1_fang.^0.5;
sigma_x2=sigma_x2_fang.^0.5;
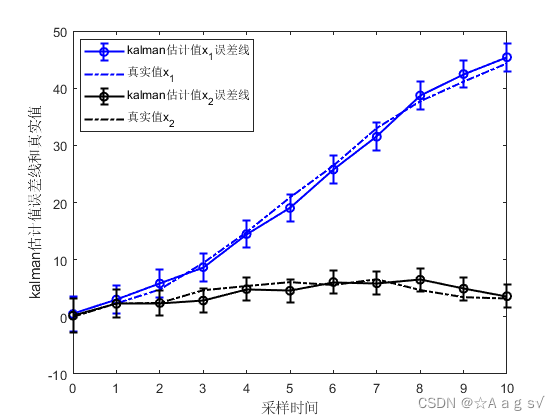
errorbar(t, X_kf(1,:),3.*sigma_x1,'-ob','LineWidth',1.5);hold on
plot(t,X(1,:),'-.b','LineWidth',1.5);hold on
errorbar(t, X_kf(2,:),3.*sigma_x2,'-ok','LineWidth',1.5);hold on
plot(t,X(2,:),'-.k','LineWidth',1.5);hold on
legend('kalman估计值x_1误差线','真实值x_1','kalman估计值x_2误差线','真实值x_2');
xlabel('采样时间');
ylabel('kalman估计值误差线和真实值');
仿真结果:
补充: 通过定义 F k = I − K k H F_k=I-K_kH Fk=I−KkH ,上面的推导可以还得出如下公式。
P k = P k ′ − K k H P k ′ − P k ′ H T K k T + K k ( H P k ′ H T + R ) K k T ⇔ F k P k ′ F k T + K k R K k T = P k ′ − K k H P k ′ − P k ′ H T K k T + P k ′ H T ( H P k ′ H T + R ) − 1 ( H P k ′ H T + R ) K k T = P k ′ − K k H P k ′ ⇔ P k ′ − P k ′ H T ( H P k ′ H T + R ) − 1 H P k ′ ⇔ ( ( P k ′ ) − 1 + H T R − 1 H ) − 1 = ( I − K k H ) P k ′ ⇔ F k P k ′ \begin{aligned} P_k&=P_k'-K_kHP_k'-P_k'H^TK_k^T+K_k\left( HP_k'H^T+R \right) K_k^T \Leftrightarrow F_kP_k'F_k^T+K_kRK_k^T \\ &=P_k'-K_kHP_k'-P_k'H^TK_k^T+P_k'H^T\left( HP_k'H^T+R \right) ^{-1}\left( HP_k'H^T+R \right) K_k^T \\ &=P_k'-K_kHP_k' \Leftrightarrow P_k' -P_k'H^T\left( HP_k'H^T+R \right) ^{-1}HP_k' \Leftrightarrow ((P_k')^{-1}+H^TR^{-1}H) ^{-1}\\ &=\left( I-K_kH \right) P_k' \Leftrightarrow F_kP_k' \end{aligned} Pk=Pk′−KkHPk′−Pk′HTKkT+Kk(HPk′HT+R)KkT⇔FkPk′FkT+KkRKkT=Pk′−KkHPk′−Pk′HTKkT+Pk′HT(HPk′HT+R)−1(HPk′HT+R)KkT=Pk′−KkHPk′⇔Pk′−Pk′HT(HPk′HT+R)−1HPk′⇔((Pk′)−1+HTR−1H)−1=(I−KkH)Pk′⇔FkPk′
K k K_k Kk的另一种形式如下,详细推导见信息滤波推导
K k = P k ′ H T ( H P k ′ H T + R ) − 1 = P k H T R − 1 \begin{aligned} K_k&=P_k'H^T\left( HP_k'H^T+R \right) ^{-1} \\ &=P_kH^TR^{-1} \end{aligned} Kk=Pk′HT(HPk′HT+R)−1=PkHTR−1
所以卡尔曼滤波还有另一种格式的递推公式
{
P
k
=
(
(
P
k
′
)
−
1
+
H
T
R
−
1
H
)
−
1
K
k
=
P
k
H
T
R
−
1
x
^
k
=
x
^
k
′
+
K
k
(
y
k
−
H
x
^
k
′
)
x
^
k
′
=
A
x
^
k
−
1
+
B
u
k
P
k
′
=
A
P
k
−
1
A
T
+
C
Q
C
T
\left\{\begin{aligned} P_k&=((P_k')^{-1}+H^TR^{-1}H)^{-1} \\ K_k&=P_kH^TR^{-1} \\ \hat{x}_k&=\hat{x}_k'+K_k\left( y_k-H\hat{x}_k' \right) \\ \hat{x}_k'&=A\hat{x}_{k-1}+Bu_k \\ P_k'&=AP_{k-1}A^T+CQC^T \end{aligned}\right.
⎩
⎨
⎧PkKkx^kx^k′Pk′=((Pk′)−1+HTR−1H)−1=PkHTR−1=x^k′+Kk(yk−Hx^k′)=Ax^k−1+Buk=APk−1AT+CQCT
另外通过定义 S = H T R − 1 H , z k = H T R − 1 y k S=H^TR^{-1}H,z_k=H^TR^{-1}y_k S=HTR−1H,zk=HTR−1yk ,还可以得到一种信息滤波器,如下。
{ S = H T R − 1 H z k = H T R − 1 y k P k = ( ( P k ′ ) − 1 + S ) − 1 x ^ k = x ^ k ′ + P k ( z k − S x ^ k ′ ) x ^ k ′ = A x ^ k − 1 + B u k P k ′ = A P k − 1 A T + C Q C T \left\{\begin{aligned} S&=H^TR^{-1}H\\ z_k&=H^TR^{-1}y_k \\ P_k&=((P_k')^{-1}+S)^{-1} \\ \hat{x}_k&=\hat{x}_k'+P_k\left( z_k-S\hat{x}_k' \right) \\ \hat{x}_k'&=A\hat{x}_{k-1}+Bu_k \\ P_k'&=AP_{k-1}A^T+CQC^T \end{aligned}\right. ⎩ ⎨ ⎧ SzkPkx^kx^k′Pk′=HTR−1H=HTR−1yk=((Pk′)−1+S)−1=x^k′+Pk(zk−Sx^k′)=Ax^k−1+Buk=APk−1AT+CQCT
下一篇:信息滤波推导






















 1390
1390











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








