原文出处:http://blog.csdn.net/renshengrumenglibing/article/details/8619827
机器人定位的目的是为了知道“自己在什么地方”,目前,机器人定位的方法可以分为非自主定位与自
主定位两大类。所谓非自主定位是在定位的过程中机器人需要借助机器人本身以外的装置如:全球定位
系统(GPS)、全局视觉系统等进行定位;自主定位是机器人仅依靠机器人本身携带的传感器进行定位。
由于在室内环境中,不能使用GPS,而安装其它的辅助定位系统比较麻烦。因此机器人一般采用自主
定位的方法。
按照初始位姿是否已知,可把机器人自主定位分为初始位姿已知的位姿跟踪(Pose tracking)和初始位
姿未知的全局定位(Global localization)。
位姿跟踪是在已知机器人的初始位姿的条件下,在机器人的运动过程中通过将观测到的特征与地图中
的特征进行匹配,求取它们之间的差别,进而更新机器人的位姿的机器人定位方法。位姿跟踪通常采用扩
展卡尔曼滤波器(Extended Kalman Filter,EKF)来实现。该方法采用高斯分布来近似地表示机器人位姿
的后验概率分布,其计算过程主要包括三步:首先是根据机器人的运模型预测机器人的位姿,然后将观测
信息与地图进行匹配,最后根据预测后的机器人位姿以及匹配的特征计算机器人应该观测到的信息,并利
用应该观测到的信息与实际观测到的信息之间的差距来更新机器人的位姿。
全局定位是在机器人的初始位姿不确定的条件下,利用局部的、不完全的观测信息估计机器人的当前
位姿。能否解决最典型而又最富挑战性的“绑架恢复”问题在一定程度上反应了机器人全局定位方法的鲁棒
性与可靠性。
一、移动机器人 SLAM 技术
可靠的定位性能是自主移动系统的关键要素。传统的定位方法是基于里程计估计的,存在不可避免的
定位误差。自从移动机器人诞生以来,对定位问题的研究就和地图创建问题密切关联,已知环境地图的定
位问题和已知定位的地图创建问题已经被广泛研究,提出了多种有效的解决途径。当地图和机器人的位置
都事先未知时,问题就变得更加复杂,出现了许多独有的新特征。在这种情况下,要求机器人在一个完全
未知的环境中从一个未知的位置出发,在递增地建立环境的导航地图同时,利用已建立的地图来同步刷新
自身的位置。该问题被称作同步定位和构图,简称 SLAM。在 SLAM 问题中,机器人位置和地图两者的估
算是高度相关的,任何一方都无法独立获取,这样形成了一种相辅相生、不断迭代的过程,因此有些学者
将其比作“鸡与蛋”问题。
近年来,移动机器人 SLAM 技术获得显著进步,被认为是解决环境未知和传感器信息不确定条件下的
移动机器人自主导航的最有效的技术之一。SLAM 基本思想是利用已创建地图修正基于运动模型的机器人
位姿估计误差;同时根据可靠的机器人位姿,创建出精度更高的地图。
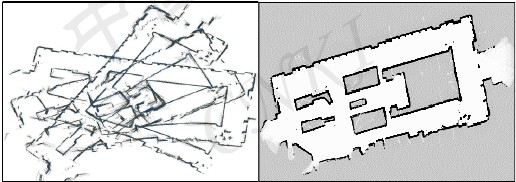
关于传感器的不确定,以最常见的里程计为例,其典型的误差积累如图 所示,其中,左图是独立
利用里程计定位、独立利用激光传感器感知环境所创建的地图,由于没有进行里程计误差补偿,几次创
建的地图差异很大,与实际环境也不符;右图是采用 SLAM 创建的地图,基于 SLAM 可以利用已创建的
地图修正里程计的误差,这样机器人的位姿误差就不会随着机器人的运动距离的增大而无限制增长,因
此可以创建精度更高的地图,也同时解决了未知环境中的机器人定位问题。
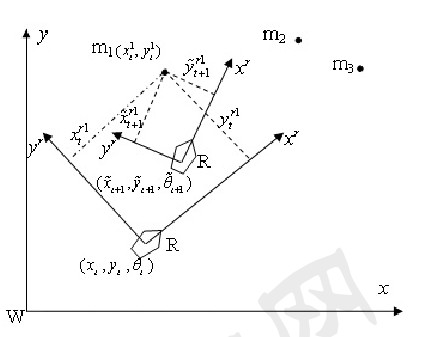
SLAM中,系统的状态由机器人的位姿和地图信息(特征的位置信息)组成。假设机器人在t时刻观测到
特征m1,如图2所示。根据观测信息只能获得特征m1在机器人坐标系R中的坐标。机器人需要估计机器
人自己本身在世界坐标系W中的位姿,然后通过坐标变换才能计算特征的世界坐标。可见在
地图创建的过
程中,必须计算机器人的位姿,也就是进行机器人的定位。然而,根据里程计获得的机器人位置信息很不
准确,显然错误的位置信息将会导致地图的不准确。
//SLAM示意图
在初始时刻,激光雷达创建的地图中并没有任何的特征。当机器人观测到某特征m时,可以根据
机器人的位姿,以及特征在机器人坐标系下的位姿,计算出特征在世界坐标系下的位姿,此时将特征
加入到地图中(更新地图);当机器人位姿改变,再次观测到特征m,可以根据特征在世界坐标系下
的位姿和特征在机器人坐标系下的位姿,解算出当前机器人的位姿(机器人定位)。
当机器人继续运动时,它将观测到更多的特征,根据同样的方法。机器人会把它们加入到地图中,
并且根据观测到的信息更新机器人的位姿以及它们的世界坐标。简单的说,SLAM利用观测到的特征计
算它们的世界坐标以实现地图创建,同时更新机器人的位姿以实现机器人的定位。
SLAM方法有很多种,主要包括基于扩展卡尔曼滤波的SLAM技术,基于传统粒子滤波的SLAM技术,
快速SLAM技术,基于扫描匹配的SLAM技术等等。
1.1基于扫描匹配的 SLAM 技术
基于扫描匹配的 SLAM是基于最近邻扫描匹配来估计两次扫描间机器人的平移和旋转的算法。扫描
匹配算法主要源自迭代最近点(Iterative Closest Point, ICP)算法及其改进算法。该算法通过迭代细调由
机器人里程计给出的初始位姿,限定了搜索空间。然而,该算法假定机器人的初始位姿和机器人的真实
位姿之间的偏差足够小,以便于达到全局最优匹配。
1.2 范例 :
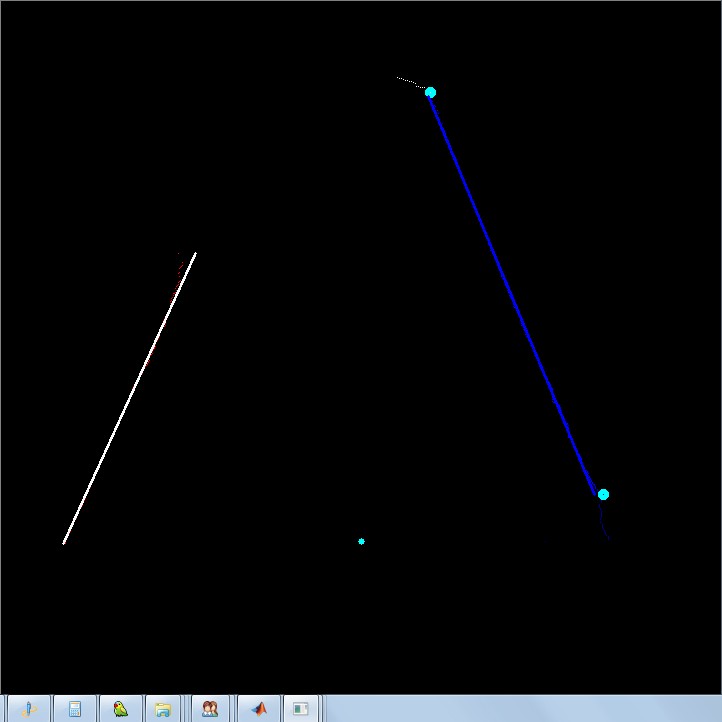
已知两条直线在激光雷达坐标系下和全局坐标系下的直线方程,求激光雷达在全局坐标下
的位置(x,y)和姿态theta
实际上已知两条直线求解是多解的,当theta是真实解,那么theta+pi同样是方程组的解,此时
可以引入新的约束,激光雷达实际上看到的两条直线,只能是直线交叉点一侧的部分,那么求解之
后可以进行验证,进而排除一个解,此时解唯一。
假设直线L1 全局下的坐标方程分别为y = a1*x + b,在雷达坐标系的方程y = a2*x+b2;
倾斜角分别为thetaW和thetaR,那么由转角alpha+ thetaR = thetaW => alpha = thetaW - thetaR;
[Xw] [cos(alpha)-sin(alpha)]XrTx
= *+
[Yw] [sin(alpha) cos(alpha)]YrTy
由两条直线解出格子坐标系下的交点,代入上式可以解出Tx Ty,上式中都是矩阵计算,由于没有word那么
强大,各位只能勉强看了。
此时实际上解释存在两个的,解出之后需要进行验证,记下线段的端点,看知否在交点的同一侧,如果在同
一侧,那么结果就是对的,否则就要再转180度。
直线的拟合参照上一篇笔记,http://blog.csdn.net/renshengrumenglibing/article/details/8604245
为了提高进度,我们可以对数据进行一次中值滤波,抑制噪声同时尽量保留数据的边沿。
//中值滤波 只能对初始的连续数据滤波
//滤波基本不丢弃数据,两端会各自扔掉几个数据
void OpenRadar::MedFilter(vector<int>& RadarRho, vector<double>& RadarTheta){
vector<int>rho;
vector<double>theta;
int halfWindowSize = 2;
int *neighbor = new int[2*halfWindowSize+1];
int temp;
for (int i = halfWindowSize; i< (int)RadarRho.size() - halfWindowSize;i++)
{
for (int j = -halfWindowSize;j <= halfWindowSize;j++)
{
neighbor[j + halfWindowSize] = RadarRho.at(i + j);
}
//排序
for (int m = 0; m < 2*halfWindowSize +1;m++)
{
for (int n = m + 1;n < 2*halfWindowSize + 1;n++)
{
if (neighbor[m]> neighbor[n])
{
temp = neighbor[m];
neighbor[m] = neighbor[n];
neighbor[n] = temp;
}
}
}
rho.push_back(neighbor[halfWindowSize]);
theta.push_back(RadarTheta.at(i));
}
RadarRho.clear();
RadarTheta.clear();
for (int i = 0; i < (int)(rho.size());i++)
{
RadarRho.push_back(rho.at(i));
RadarTheta.push_back(theta.at(i));
}
}//已知四条直线如何计算变换参数
void Coordinate::CalCoorTransPara(CoorTransPara &transPara,
LinePara W1,
LinePara W2,
LinePara R1,
LinePara R2)
{
double theta = ( W1.Rho - R1.Rho + W2.Rho - R2.Rho )/2;
//double theta = ( W1.Rho - R1.Rho);
//求解出Xw Yw Xr Yr
double Xw = (double)(W1.b - W2.b)/(W2.a - W1.a);
double Yw = W1.a*Xw + W1.b;
double Xr = (double)(R1.b - R2.b)/(R2.a - R1.a);
double Yr = R1.a*Xr + R1.b;
int Tx = (int)(Xw - cos(theta)*Xr + sin(theta)*Yr);
int Ty = (int)(Yw - sin(theta)*Xr - cos(theta)*Yr);
//交点判定,场地上的几条直线都是有角点的
iPoint crossPoint;//交点
iPoint vectorW1,vectorR1;//向量
//iPoint vectorR2,vectorW2;
if (W1.startPoint.x == W2.startPoint.x && W1.startPoint.y == W2.startPoint.y)
{
crossPoint = ipoint(W1.startPoint.x,W1.startPoint.y);
vectorW1 = ipoint(W1.endPoint.x - W1.startPoint.x, W1.endPoint.y - W1.startPoint.y);
//vectorW2 = ipoint(W2.endPoint.x - W2.startPoint.x, W2.endPoint.y - W2.startPoint.y);
}else if (W1.endPoint.x == W2.startPoint.x && W1.endPoint.y == W2.startPoint.y)
{
crossPoint = ipoint(W1.endPoint.x,W1.endPoint.y);
vectorW1 = ipoint(W1.startPoint.x - W1.endPoint.x, W1.startPoint.y - W1.endPoint.y);
//vectorW2 = ipoint(W2.endPoint.x - W2.startPoint.x, W2.endPoint.y - W2.startPoint.y);
}else if (W1.startPoint.x == W2.endPoint.x && W1.startPoint.y == W2.endPoint.y)
{
crossPoint = ipoint(W1.startPoint.x,W1.startPoint.y);
vectorW1 = ipoint(W1.endPoint.x - W1.startPoint.x, W1.endPoint.y - W1.startPoint.y);
//vectorW2 = ipoint(W2.startPoint.x - W2.endPoint.x, W2.startPoint.y - W2.endPoint.y);
}else if (W1.endPoint.x == W2.endPoint.x && W1.endPoint.y == W2.endPoint.y)
{
crossPoint = ipoint(W1.endPoint.x,W1.endPoint.y);
vectorW1 = ipoint(W1.startPoint.x - W1.endPoint.x, W1.startPoint.y - W1.endPoint.y);
//vectorW2 = ipoint(W2.startPoint.x - W2.endPoint.x, W2.startPoint.y - W2.endPoint.y);
}
//将激光雷达下的两个点旋转到W系下
transPara.theta = theta;
transPara.Tx = Tx;
transPara.Ty = Ty;
iPoint R1ToW;
//iPoint R2ToW;
TransformCoord(transPara,R1.startPoint,R1ToW);
//TransformCoord(transPara,R2.startPoint,R2ToW);
vectorR1.x = R1ToW.x - crossPoint.x;
vectorR1.y = R1ToW.y - crossPoint.y;
//判断是否在同一侧?
if (vectorW1.x * vectorR1.x + vectorW1.y*vectorR1.y < 0)
{
//旋转角度差了180度,需要调转180度
transPara.theta = theta + PI;
transPara.Tx = (int)(Xw - cos(transPara.theta)*Xr + sin(transPara.theta)*Yr);
transPara.Ty = (int)(Yw - sin(transPara.theta)*Xr - cos(transPara.theta)*Yr);
}else{
}
//数据测试
/* TransformCoord(transPara,R1.startPoint,R1ToW);
cout<<"R1ToW.x "<<R1ToW.x<<" R1ToW.y "<<R1ToW.y<<endl;
TransformCoord(transPara,R1.endPoint,R1ToW);
cout<<"R1ToW.x "<<R1ToW.x<<" R1ToW.y "<<R1ToW.y<<endl;
TransformCoord(transPara,R2.startPoint,R2ToW);
cout<<"R2ToW.x "<<R2ToW.x<<" R2ToW.y "<<R2ToW.y<<endl;
TransformCoord(transPara,R2.endPoint,R2ToW);
cout<<"R2ToW.x "<<R2ToW.x<<" R2ToW.y "<<R2ToW.y<<endl;*/
//进行一次验证,看看交点进行坐标变换之后是否接近匹配的点
/* iPoint R = ipoint(Xr,Yr);
iPoint R2W;
TransformCoord(transPara,R,R2W);
cout<<"R2W.x "<<R2W.x<<" R2W.y "<<R2W.y<<endl;*/
}//完整的Coordinate.h
#pragma once
#include "WeightedFit.h"
#include <iostream>
using namespace std;
//场地中的关键点
static iPoint FieldPointA = ipoint(9192,0);
static iPoint FieldPointB = ipoint(0,9192);
static iPoint FieldPointC = ipoint(-9192,0);
static iPoint FieldPointD = ipoint(0,-9192);
//场地中的直线变量
static LinePara FieldLine1 = linePara(-1.0,9192.3881554,FieldPointA,FieldPointB);
static LinePara FieldLine2 = linePara(1.0,9192.3881554,FieldPointB,FieldPointC);
static LinePara FieldLine3 = linePara(-1.0,-9192.3881554,FieldPointC,FieldPointD);
static LinePara FieldLine4 = linePara(1.0,-9192.3881554,FieldPointD,FieldPointA);
static LinePara FieldLine5 = linePara(100000.0,0.0,FieldPointB,FieldPointD);
//场地中的圆
static CirclePara FieldCircle1 = circlePara(-3000,1301,400,350);
static CirclePara FieldCircle2 = circlePara(-1951,880,400,350);
static CirclePara FieldCircle3 = circlePara(-651,815,400,350);
static CirclePara FieldCircle4 = circlePara(-495,2416,400,350);
static CirclePara FieldCircle5 = circlePara(-3347,-997,400,350);
static CirclePara FieldCircle6 = circlePara(-2400,-2848,400,350);
static CirclePara FieldCircle7 = circlePara(-1499,-2499,400,350);
static CirclePara FieldCircle8 = circlePara(3000,1301,400,350);
static CirclePara FieldCircle9 = circlePara(1951,880,400,350);
static CirclePara FieldCircle10 = circlePara(651,815,400,350);
static CirclePara FieldCircle11= circlePara(495,2416,400,350);
static CirclePara FieldCircle12 = circlePara(3347,-997,400,350);
static CirclePara FieldCircle13 = circlePara(2400,-2848,400,350);
static CirclePara FieldCircle14 = circlePara(1499,-2499,400,350);
//坐标系类,进行坐标系相关的计算
typedef struct{
int Tx;
int Ty;
double theta;//旋转角
}CoorTransPara; //坐标变换参数
class Coordinate
{
public:
Coordinate(void);
~Coordinate(void);
//已知四条直线如何计算变换参数
void CalCoorTransPara(CoorTransPara &transPara,
LinePara W1,
LinePara W2,
LinePara R1,
LinePara R2);
void CoortransTest();
void CalRadarCoord();
CoorTransPara RadarCoordTransPara;//全局坐标系和雷达坐标系之间的转换参数
void printRadarCoordtransPara(CoorTransPara coordtrans);
void TransformCoord(CoorTransPara transPara,iPoint R,iPoint& W);
};
#include "Coordinate.h"
Coordinate::Coordinate(void)
{
}
Coordinate::~Coordinate(void)
{
}
//已知四条直线如何计算变换参数
void Coordinate::CalCoorTransPara(CoorTransPara &transPara,
LinePara W1,
LinePara W2,
LinePara R1,
LinePara R2)
{
double theta = ( W1.Rho - R1.Rho + W2.Rho - R2.Rho )/2;
//double theta = ( W1.Rho - R1.Rho);
//求解出Xw Yw Xr Yr
double Xw = (double)(W1.b - W2.b)/(W2.a - W1.a);
double Yw = W1.a*Xw + W1.b;
double Xr = (double)(R1.b - R2.b)/(R2.a - R1.a);
double Yr = R1.a*Xr + R1.b;
int Tx = (int)(Xw - cos(theta)*Xr + sin(theta)*Yr);
int Ty = (int)(Yw - sin(theta)*Xr - cos(theta)*Yr);
//交点判定,场地上的几条直线都是有角点的
iPoint crossPoint;//交点
iPoint vectorW1,vectorR1;//向量
//iPoint vectorR2,vectorW2;
if (W1.startPoint.x == W2.startPoint.x && W1.startPoint.y == W2.startPoint.y)
{
crossPoint = ipoint(W1.startPoint.x,W1.startPoint.y);
vectorW1 = ipoint(W1.endPoint.x - W1.startPoint.x, W1.endPoint.y - W1.startPoint.y);
//vectorW2 = ipoint(W2.endPoint.x - W2.startPoint.x, W2.endPoint.y - W2.startPoint.y);
}else if (W1.endPoint.x == W2.startPoint.x && W1.endPoint.y == W2.startPoint.y)
{
crossPoint = ipoint(W1.endPoint.x,W1.endPoint.y);
vectorW1 = ipoint(W1.startPoint.x - W1.endPoint.x, W1.startPoint.y - W1.endPoint.y);
//vectorW2 = ipoint(W2.endPoint.x - W2.startPoint.x, W2.endPoint.y - W2.startPoint.y);
}else if (W1.startPoint.x == W2.endPoint.x && W1.startPoint.y == W2.endPoint.y)
{
crossPoint = ipoint(W1.startPoint.x,W1.startPoint.y);
vectorW1 = ipoint(W1.endPoint.x - W1.startPoint.x, W1.endPoint.y - W1.startPoint.y);
//vectorW2 = ipoint(W2.startPoint.x - W2.endPoint.x, W2.startPoint.y - W2.endPoint.y);
}else if (W1.endPoint.x == W2.endPoint.x && W1.endPoint.y == W2.endPoint.y)
{
crossPoint = ipoint(W1.endPoint.x,W1.endPoint.y);
vectorW1 = ipoint(W1.startPoint.x - W1.endPoint.x, W1.startPoint.y - W1.endPoint.y);
//vectorW2 = ipoint(W2.startPoint.x - W2.endPoint.x, W2.startPoint.y - W2.endPoint.y);
}
//将激光雷达下的两个点旋转到W系下
transPara.theta = theta;
transPara.Tx = Tx;
transPara.Ty = Ty;
iPoint R1ToW;
//iPoint R2ToW;
TransformCoord(transPara,R1.startPoint,R1ToW);
//TransformCoord(transPara,R2.startPoint,R2ToW);
vectorR1.x = R1ToW.x - crossPoint.x;
vectorR1.y = R1ToW.y - crossPoint.y;
//判断是否在同一侧?
if (vectorW1.x * vectorR1.x + vectorW1.y*vectorR1.y < 0)
{
//旋转角度差了180度,需要调转180度
transPara.theta = theta + PI;
transPara.Tx = (int)(Xw - cos(transPara.theta)*Xr + sin(transPara.theta)*Yr);
transPara.Ty = (int)(Yw - sin(transPara.theta)*Xr - cos(transPara.theta)*Yr);
}else{
}
//数据测试
/* TransformCoord(transPara,R1.startPoint,R1ToW);
cout<<"R1ToW.x "<<R1ToW.x<<" R1ToW.y "<<R1ToW.y<<endl;
TransformCoord(transPara,R1.endPoint,R1ToW);
cout<<"R1ToW.x "<<R1ToW.x<<" R1ToW.y "<<R1ToW.y<<endl;
TransformCoord(transPara,R2.startPoint,R2ToW);
cout<<"R2ToW.x "<<R2ToW.x<<" R2ToW.y "<<R2ToW.y<<endl;
TransformCoord(transPara,R2.endPoint,R2ToW);
cout<<"R2ToW.x "<<R2ToW.x<<" R2ToW.y "<<R2ToW.y<<endl;*/
//进行一次验证,看看交点进行坐标变换之后是否接近匹配的点
/* iPoint R = ipoint(Xr,Yr);
iPoint R2W;
TransformCoord(transPara,R,R2W);
cout<<"R2W.x "<<R2W.x<<" R2W.y "<<R2W.y<<endl;*/
}
void Coordinate::CoortransTest(){
Coordinate coord;
CoorTransPara coordtrans;
coord.CalCoorTransPara(coordtrans,FieldLine1,FieldLine5,FieldLine2,FieldLine5);
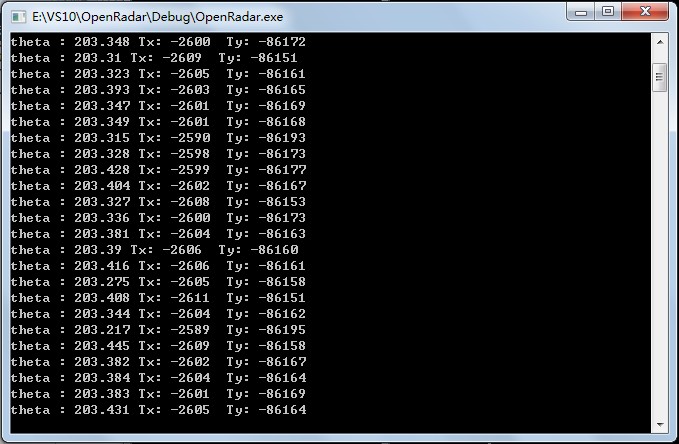
cout<<"theta : "<<coordtrans.theta*180/PI<<" Tx: "<<coordtrans.Tx<<" Ty: "<<coordtrans.Ty<<endl;
}
void Coordinate::printRadarCoordtransPara(CoorTransPara coordtrans){
cout<<"theta : "<<coordtrans.theta*180/PI<<" Tx: "<<coordtrans.Tx<<" Ty: "<<coordtrans.Ty<<endl;
}
void Coordinate::TransformCoord(CoorTransPara transPara,iPoint R,iPoint& W){
W.x = (int)(R.x*cos(transPara.theta) - R.y*sin(transPara.theta) );
W.y = (int)(R.x*sin(transPara.theta) + R.y*cos(transPara.theta) );
W.x = W.x + transPara.Tx ;
W.y = W.y + transPara.Ty ;
}























 4077
4077

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








