作者 | 小龙爱学习 编辑 | 汽车人
原文链接:https://zhuanlan.zhihu.com/p/648271918
点击下方卡片,关注“自动驾驶之心”公众号
ADAS巨卷干货,即可获取
点击进入→自动驾驶之心【轨迹预测】技术交流群
后台回复【轨迹预测综述】获取行人、车辆轨迹预测等相关最新论文!
本文只做学术分享,如有侵权,联系删文
今天先热热身,进行一波基础知识回顾——学习一下曲线插值算法中的五次多项式曲线插值方法。
其实在深度学习轨迹预测领域,通常不会直接使用传统的曲线插值算法。一般深度学习模型可以通过学习大量轨迹数据来预测未来的轨迹,而不需要显式地进行曲线插值。深度学习模型能够从数据中学习到轨迹的非线性特征和规律,并生成符合这些规律的连续轨迹。
然而,曲线插值算法仍在以下情况下可能会被轨迹预测领域用到(但其实更多的被用于路径规划领域):
轨迹预测通常会和高精地图信息相结合,在高精地图车道线等相关的数据处理中,往往会大量运用到曲线插值算法;
在一些特定场景下,可以将曲线插值算法与深度学习模型结合使用。例如,当训练数据较少或存在缺失值时,可以使用曲线插值算法填充缺失的轨迹数据,以增加训练数据的数量或完整性。这样可以提高深度学习模型的性能和鲁棒性。
因此作为一个领域相关基础知识,在自动驾驶轨迹预测算法系列文章中,我们首先来回顾一下常用的曲线插值算法,本文主要介绍五次多项式曲线插值。
声明
本文主要是针对大佬CODspielen的下面这篇文章的学习笔记,笔者主要针对其中的关键点进行摘要、记录,并将原作中的Windows版本程序移植到Linux系统中,将可视化库从Windows系统中的easyX改为Linux系统中的Pangolin,同时根据自己的理解添加了若干注释。原文链接如下:
CODspielen:【决策规划算法】曲线插值算法:五次多项式(C++)
https://zhuanlan.zhihu.com/p/546222927
解决的问题
车辆在某些特定约束下(安全避障、快速、路线短、体感等),需要进行路径的曲线拟合,我们通过路径曲线拟合来学习五次多项式插值算法的实际应用。
该问题下,通常已知当前自车的状态(位置、航向角、速度、加速度等)以及目标位置的自车期望状态,这些状态通常可以作为待拟合路径曲线的约束条件,常用的曲线有多项式曲线,双圆弧段曲线,正统函数曲线,贝塞尔曲线,B样条曲线等。
解决路径曲线拟合的核心思想:
选定待拟合的曲线类型;
根据自车状态(位置、航向角、速度、加速度等)以及车辆期望达到的状态,将这些状态量作为边界条件代入曲线方程进行求解,求出曲线相关系数;
利用曲线系数,根据时间间隔对曲线进行采样,得到的采样点即为拟合后的路径点。
本文中的代码最终效果如下(只关注轨迹曲线插值,忽略了车辆控制和航向角规划等细节):

关键点笔记
五次多项式是指横向/纵向位置关于时间 t 的五次多项式,而不是横向位置y关于纵向位置x的五次多项式:

假设起点、终点的位置、速度(一阶导)、加速度(二阶导)均已知,有已下方程:

以上共12个方程,其中12个未知数(a0 - a5, b0 - b5),可以通过线性方程组求出唯一解, 即:
X = A * T,Y = B * T
求解A、B,即为曲线系数,后续根据时间 t 采样,即可得到曲线上的路径点,具体请参考代码。
注意:五次多项式插值速度曲线并没有匀速段,因此这种规划方式不适用于笛卡尔空间的要求匀速的场合的规划。
代码
以下为C++程序代码,在Linux系统下利用CMake编译,共三个文件:interpolation.h、interpolation.cpp、CMakeLists.txt,代码本人也上传到了Github仓库:
github.com/xiaolong361/interpolation/tree/main/quintic_polynomial
,可以参考其中的Readme直接编译。
代码中注释比较详细,因此其中的实现细节本文不再赘述了。需要额外注意的一点是,本文代码采用的坐标系和参考文章不同,本文采用右手系,如下图所示:

其中,红色表示x轴,正右方为正;绿色表示y轴,正前方为正;蓝色表示z轴,正上方为正。
interpolation.h:
#pragma once
#include <iostream>
#include <cmath>
#include <ctime>
#include <vector>
#include <pangolin/pangolin.h>
using namespace std;
constexpr auto N = 10; //矩阵的最大行(列)数
constexpr auto Swidth = 600;
constexpr auto Sheight = 1200;
constexpr auto deltaTIME = 50000; // us
enum DriveStatus {
state1 = 0,
state2 = 1,
ahead = 2,
turning = 3,
exiting = 4
};
class Point {
public:
double x;
double y;
};
//车辆基类
class CarBase {
public:
virtual void showCar(Point p) = 0;//绘制车辆,纯虚函数
public:
double length;//长度
double width;//宽度
Point p0;//起始位置
Point p1;//终点位置
};
//车辆
class Car :public CarBase {
public:
Car(double Rw);
void showCar(Point p);//绘制车辆
};
//障碍车辆
class CarObs :public CarBase {
public:
CarObs(double Rw);
void showCar(Point p);//绘制障碍车辆
};
//道路
class Road {
public:
Road();
~Road();
void showRoad(Point p);//绘制道路
public:
double RWidth = 100.0; // 路宽
double dot_distance = 8.0; // 虚线点的间隔
// 道路上的控制车辆
CarBase *car = new Car(RWidth);//多态:父类指针指向子类对象
// 道路上的障碍车辆
CarBase *carObs = new CarObs(RWidth);//多态:父类指针指向子类对象
};
//矩阵
class Mat {
public:
#if 0
Mat();//存在有参构造时,要手写默认构造,才能创建不带参对象
Mat(int mm, int nn);//手动创建矩阵时用
void createMat();//手动创建矩阵
#endif
void createMatT(double t0, double t1);//创建矩阵T
void createVector(double tmp1, double tmp2, double tmp3, double tmp4, double tmp5, double tmp6);//创建向量
void PrintMat();//打印矩阵
void augMat(Mat a, Mat b);//求矩阵 a 和向量 b 的增广矩阵
bool solve(Mat a, Mat b); //求线性方程组的解(ax=b ,求 x),a 为方阵 ,b 为列向量
public:
int m;
int n; //行数和列数
double mat[N][N] = { 0 }; //矩阵元素初始化
};
//多项式求解曲线
class Polynomial {
public:
Polynomial();
void SetPangolinParams(pangolin::OpenGlRenderState *camera, pangolin::View *view);
void process(); //整个过程
void CarGoStraight(); //直行
void showAheadTrack(); //绘制直行规划线轨迹
void calMat(); //计算矩阵
void showTurningTrack(int trackIndex); //绘制多项式规划线轨迹
void CarChangeLane(); //车辆换道移动
void ShowResult(); //显示速度与加速度关于时间的曲线
public:
Road road;
double t0 = 0.0;
double t1 = 3.0;
double x0 = road.car->p0.x;
double y0 = road.car->p0.y;
double x1 = road.car->p1.x;
double y1 = road.car->p1.y;
double vx0 = 0.0;
double vy0 = 120.0; // t0时y方向速度为120
double vx1 = 0.0;
double vy1 = 120.0; // t1时y方向速度为120
double ax0 = 0.0;
double ay0 = 0.0;
double ax1 = 0.0;
double ay1 = 0.0;
Mat X;
Mat Y;
Mat T;
Mat A;
Mat B;
double disS = road.car->length * 4; //纵向换道距离
double safeDis = 400.0; //纵向安全距离
int disAhead = safeDis / 50; //直行规划线的间隔
double speed = 5.0; //直行速度
double delta_t = 0.05; //时间间隔, s
vector<Point> trackPoints; //存储规划轨迹点
int curTrackIndex = -1;
DriveStatus state = state1;
pangolin::OpenGlRenderState *camera_p = nullptr;
pangolin::View *view_p = nullptr;
};interpolation.cpp:
#include "interpolation.h"
#include <unistd.h>
#include <pangolin/pangolin.h>
static void DrawLine2D(double x1, double y1, double x2, double y2, float r, float g, float b) {
glColor3f(r, g, b);
glBegin(GL_LINES);
glVertex3f(x1, y1, 0);
glVertex3f(x2, y2, 0);
glEnd();
}
static void DrawSimpleRectangle(double left, double top, double right, double bottom, float r, float g, float b) {
glColor3f(r, g, b);
glBegin(GL_LINES);
glVertex3f(left, bottom, 0);
glVertex3f(right, bottom, 0);
glVertex3f(right, bottom, 0);
glVertex3f(right, top, 0);
glVertex3f(right, top, 0);
glVertex3f(left, top, 0);
glVertex3f(left, top, 0);
glVertex3f(left, bottom, 0);
glEnd();
}
/**
* @brief Construct a new Car:: Car object
*
* @param Rw car所在的宽度位置(直行时不变)
*/
Car::Car(double Rw) {
length = 100.0;
width = 60.0;
p0.x = Rw / 2;
p0.y = length;
p1 = p0;
cout << "car loc: " << p0.x << ", " << p0.y << endl;
cout << "car target loc: " << p1.x << ", " << p1.y << endl;
}
CarObs::CarObs(double Rw) {
length = 100.0;
width = 60.0;
p0.x = Rw / 2;
p0.y = Sheight / 2 + length * 4;
p1 = p0;
cout << "carObs loc: " << p0.x << ", " << p0.y << endl;
}
//绘制车辆
void Car::showCar(Point p) {
double left = p.x - width / 2;
double right = p.x + width / 2;
double top = p.y + length / 2;
double bottom = p.y - length / 2;
DrawSimpleRectangle(left, top, right, bottom, 1.0, 0.0, 0.0);
}
//绘制障碍车辆
void CarObs::showCar(Point p) {
double left = p.x - width / 2;
double right = p.x + width / 2;
double top = p.y + length / 2;
double bottom = p.y - length / 2;
DrawSimpleRectangle(left, top, right, bottom, 1.0, 0.0, 0.0);
}
Road::Road() {
showRoad(car->p0);
}
Road::~Road()
{
if (car != nullptr) {
delete car;
car = nullptr;
}
if (carObs != nullptr) {
delete car;
carObs = nullptr;
}
}
/**
* @brief 绘制道路
*
* @param p 道路上car的位置
*/
void Road::showRoad(Point p) {
//绘制道路中心
glBegin(GL_POINTS);
glColor3f(0.f, 0.8f, 0.f); // R,G,B
int point_num = Sheight / dot_distance + 1;
double start_y = 0;
for (int i = 0; i < point_num; i++) {
start_y += dot_distance;
glVertex3f(0, start_y, 3);
}
glEnd(); // 结束绘图
//绘制左右边界
glBegin(GL_LINES);
glLineWidth(3);//设置线宽
DrawLine2D(0. - RWidth, 0.0,
0. - RWidth, Sheight,
0.f,0.8f,0.f);
DrawLine2D(RWidth, 0.0,
RWidth, Sheight,
0.f,0.8f,0.f);
car->showCar(p);
carObs->showCar(carObs->p0);
}
//创建矩阵T
void Mat::createMatT(double t0, double t1) {
m = n = 6;
for (int j = 1; j <= n; j++) {
mat[1][j] = pow(t0, n - j);
mat[2][j] = (n - j) * pow(t0, n - j - 1);
mat[3][j] = (n - j) * (n - j - 1) * pow(t0, n - j - 2);
if (n - j - 1 < 0) {
mat[2][j] = 0.0;
}
if (n - j - 2 < 0) {
mat[3][j] = 0.0;
}
}
for (int j = 1; j <= n; j++) {
mat[4][j] = pow(t1, n - j);
mat[5][j] = (n - j) * pow(t1, n - j - 1);
mat[6][j] = (n - j) * (n - j - 1) * pow(t1, n - j - 2);
if (n - j - 1 < 0) {
mat[5][j] = 0.0;
}
if (n - j - 2 < 0) {
mat[6][j] = 0.0;
}
}
}
//创建向量
void Mat::createVector(double tmp1, double tmp2, double tmp3, double tmp4, double tmp5, double tmp6) {
m = 6;
n = 1;
mat[1][1] = tmp1;
mat[2][1] = tmp2;
mat[3][1] = tmp3;
mat[4][1] = tmp4;
mat[5][1] = tmp5;
mat[6][1] = tmp6;
}
//打印矩阵
void Mat::PrintMat() {
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
cout << mat[i][j] << "\t";
}
cout << endl;
}
cout << endl;
}
//求矩阵 a 和向量 b 的增广矩阵
void Mat::augMat(Mat a, Mat b) {
m = a.m;
n = a.n + 1; //列数+1
for (int i = 1; i <= a.m; i++) {
for (int j = 1; j <= a.n; j++) {
mat[i][j] = a.mat[i][j];
}
mat[i][n] = b.mat[i][1]; //每行的最后一列,赋值为向量b在这一行的元素
}
}
//求线性方程组的解(ax=b ,求 x),a 为方阵 ,b 为列向量 //矩阵 a 为方阵并且方程组有唯一解时返回 true
bool Mat::solve(Mat a, Mat b) {
if (a.n != a.m) { //只求解是方阵时的情形
cout << "系数矩阵不是方阵" << endl;
return false;
}
m = a.n;
n = 1; //解向量中必定有 a.n( a.m )个分量,是 a.n * 1 的列向量
Mat aa;
aa.augMat(a, b); //求增广矩阵
cout << "增广矩阵是:" << endl;
aa.PrintMat();
//下面代码将增广矩阵化为上三角矩阵,并判断增广矩阵秩是否为 n
for (int i = 1; i <= aa.m; i++) {
//寻找第 i 列不为零的元素
int k;
for (k = i; k <= aa.m; k++) {
if (fabs(aa.mat[k][i]) > 1e-10) { //满足这个条件时,认为这个元素不为0
break;
}
}
if (k <= aa.m) { //说明第 i 列有不为0的元素
//交换第 i 行和第 k 行所有元素
for (int j = i; j <= aa.n; j++) { //从第 i 个元素交换即可,因为前面的元素都为0
aa.mat[0][j] = aa.mat[i][j]; aa.mat[i][j] = aa.mat[k][j]; aa.mat[k][j] = aa.mat[0][j];//使用aa.mat[0][j]作为中间变量交换元素
}
double c;//倍数
for (int j = i + 1; j <= aa.m; j++) {
c = -aa.mat[j][i] / aa.mat[i][i];
for (k = i; k <= aa.n; k++) {
aa.mat[j][k] += c * aa.mat[i][k];//第 i 行 a 倍加到第 j 行
}
}
}
else { //没有找到则说明系数矩阵秩不为 n ,说明方程组中有效方程的个数小于 n
cout << "系数矩阵奇异,线性方程组无解或有无数解" << endl;
return false;
}
}
//自下而上求解
for (int i = a.m; i >= 1; i--) {
mat[i][1] = aa.mat[i][aa.n];
for (int j = a.m; j > i; j--) {
mat[i][1] -= mat[j][1] * aa.mat[i][j];
}
mat[i][1] /= aa.mat[i][i];
}
return true;
}
Polynomial::Polynomial() {
//如果是行进过程中换道,就在决定要换道的时候再计算矩阵;
showAheadTrack();
}
//车辆直行,当status为DriveStatus::ahead时执行
void Polynomial::CarGoStraight() {
if (state != DriveStatus::ahead || camera_p == nullptr || view_p == nullptr) {
return;
}
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
view_p->Activate(*camera_p);
// 更新道路上car的位置并显示
road.car->p0.y += speed;
road.car->p1.y += speed;
showAheadTrack();
road.showRoad(road.car->p0);
glEnd(); // 结束绘图
if (abs(road.car->p0.x - road.carObs->p0.x) <= road.RWidth/2.0 &&
abs(road.car->p0.y - road.carObs->p0.y) <= safeDis) {
this->state = DriveStatus::turning;
}
if (road.car->p0.y > Sheight) {
this->state = DriveStatus::exiting;
}
usleep(deltaTIME);
}
//绘制直行规划线轨迹
void Polynomial::showAheadTrack() {
glBegin(GL_POINTS);
glColor3f(0.f, 0.f, 0.8f); // R,G,B
Point pt = road.car->p0;
for (int i = 0; i < 50; i++) {
pt.y += disAhead;
glVertex3f(pt.x, pt.y, 3);
}
glEnd(); // 结束绘图
}
//计算矩阵
void Polynomial::calMat() {
x0 = road.car->p0.x;
y0 = road.car->p0.y;
road.car->p1.x = 0. - road.RWidth / 2;
road.car->p1.y = road.car->p0.y + disS;
x1 = road.car->p1.x;
y1 = road.car->p1.y;
cout << x0 << ", " << y0 << ", " << x1 << ", " << y1 << endl;
X.createVector(x0, vx0, ax0, x1, vx1, ax1);
Y.createVector(y0, vy0, ay0, y1, vy1, ay1);
T.createMatT(t0, t1);
cout << endl;
cout << "X向量:" << endl;
X.PrintMat();
cout << "Y向量:" << endl;
Y.PrintMat();
cout << "T矩阵:" << endl;
T.PrintMat();
if (A.solve(T, X)) { // T * A = X
cout << "求得的A向量如下:" << endl;
A.PrintMat();
}
if (B.solve(T, Y)) { // T * B = Y
cout << "求得的B向量如下:" << endl;
B.PrintMat();
}
}
//绘制多项式轨迹
void Polynomial::showTurningTrack(int trackIndex) {
if (trackIndex < 0 || trackIndex >= trackPoints.size()) {
return;
}
glBegin(GL_POINTS);
glColor3f(0.f, 0.f, 1.0f); // R,G,B
for (int i = trackIndex; i < trackPoints.size(); ++i) {
glVertex3f(trackPoints.at(i).x, trackPoints.at(i).y, 3);
}
glEnd(); // 结束绘图
}
//车辆换道移动,只在DriveStatus::turning状态运行
void Polynomial::CarChangeLane() {
if (state != DriveStatus::turning || camera_p == nullptr || view_p == nullptr) {
return;
}
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
view_p->Activate(*camera_p);
if (curTrackIndex == -1) { // 刚开始进入转弯状态时,计算轨迹
calMat();//计算矩阵
for (double t = t0; t <= t1; t += delta_t) { // 根据五次多项式计算轨迹
double x_tmp = A.mat[1][1] * pow(t, 5) + A.mat[2][1] * pow(t, 4) + A.mat[3][1] * pow(t, 3) + A.mat[4][1] * pow(t, 2) + A.mat[5][1] * pow(t, 1) + A.mat[6][1];
double y_tmp = B.mat[1][1] * pow(t, 5) + B.mat[2][1] * pow(t, 4) + B.mat[3][1] * pow(t, 3) + B.mat[4][1] * pow(t, 2) + B.mat[5][1] * pow(t, 1) + B.mat[6][1];
Point ptmp;
ptmp.x = x_tmp;
ptmp.y = y_tmp;
trackPoints.push_back(ptmp);
}
}
curTrackIndex++;
// cout << "curTrackIndex = " << curTrackIndex << ", trackPoints.size() = " << trackPoints.size() << endl;
if (curTrackIndex == trackPoints.size()) {
state = DriveStatus::ahead;
}
else {
// 绘制转弯轨迹
showTurningTrack(curTrackIndex);
auto &curLocation = trackPoints.at(curTrackIndex);
road.showRoad(curLocation);
//实时更新p0位置
road.car->p0.x = curLocation.x;
road.car->p0.y = curLocation.y;
}
usleep(deltaTIME);
}
//显示速度与加速度关于时间的曲线
void Polynomial::ShowResult() {
if (state != DriveStatus::exiting || camera_p == nullptr || view_p == nullptr) {
return;
}
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
pangolin::OpenGlRenderState camera(
// 图像宽度、高度、4个内参fx fy cx cy以及最近、最远视距
pangolin::ProjectionMatrix(Swidth, Sheight, 1500, 1500, 0, 0, 0.1, 2500),
/*相机的初始坐标,相机视点的初始位置(即相机光轴朝向),相机轴方向*/
pangolin::ModelViewLookAt(Swidth/2.0, 0.0, 1800, 0, Sheight/2, 0, pangolin::AxisY));
view_p->Activate(camera);
DrawLine2D(0, 0, 0,1000,1,1,1);
DrawLine2D(0, 0, 1000,0,1,1,1);
// 同时绘制x-t和y-t速度曲线
for (double t = t0; t <= t1; t += delta_t) {
double vx_tmp = 5 * A.mat[1][1] * pow(t, 4) + 4 * A.mat[2][1] * pow(t, 3) + 3 * A.mat[3][1] * pow(t, 2) + 2 * A.mat[4][1] * pow(t, 1) + A.mat[5][1];
double vy_tmp = 5 * B.mat[1][1] * pow(t, 4) + 4 * B.mat[2][1] * pow(t, 3) + 3 * B.mat[3][1] * pow(t, 2) + 2 * B.mat[4][1] * pow(t, 1) + B.mat[5][1];
glColor3f(1.0, 0., 0.);
glPointSize(5.0);
glBegin(GL_POINTS);
glVertex3f(t * 100, vx_tmp, 10);
glVertex3f(t * 100, vy_tmp, 10);
glEnd();
}
// 同时绘制x-t和y-t加速度曲线
for (double t = t0; t <= t1; t += delta_t) {
double ax_tmp = 20 * A.mat[1][1] * pow(t, 3) + 12 * A.mat[2][1] * pow(t, 2) + 6 * A.mat[3][1] * pow(t, 1) + 2 * A.mat[4][1];
double ay_tmp = 20 * B.mat[1][1] * pow(t, 3) + 12 * B.mat[2][1] * pow(t, 2) + 6 * B.mat[3][1] * pow(t, 1) + 2 * B.mat[4][1];
glColor3f(0., 1., 0.);
glPointSize(5.0);
glBegin(GL_POINTS);
glVertex3f(t * 100 + 350, ax_tmp, 10);
glVertex3f(t * 100 + 350, ay_tmp, 10);
glEnd();
}
pangolin::FinishFrame();
}
// 整个过程
void Polynomial::process() {
if (this->state == DriveStatus::ahead) {
CarGoStraight();
}
if (this->state == DriveStatus::turning) {
CarChangeLane();
}
if (this->state == DriveStatus::exiting) {
ShowResult();
}
}
void Polynomial::SetPangolinParams(pangolin::OpenGlRenderState *camera, pangolin::View *view) {
camera_p = camera;
view_p = view;
}
/**
* @brief 五次多项式例程
* 参考博客:https://zhuanlan.zhihu.com/p/546222927
* 图形化工具从easyX改为pangolin,在Ubuntu系统下开发、验证, 采用状态机控制整个仿真过程
* 五次多项式,最多能确定每个期望点的位置、速度和加速度;
* 五次多项式是指横向/纵向位置关于时间t的五次多项式,而不是横向位置y关于纵向位置x的五次多项式!
*
* x(t) = a0 + a1t + a2t^2 + a3t^3 + a4t^4 + a5t^5; //纵向位置
* y(t) = b0 + b1t + b2t^2 + b3t^3 + b4t^4 + b5t^5; //横向位置
*
* 假设起点、终点的位置、速度(一阶导)、加速度(二阶导)均已知,有已下方程:
*
* x(t0) = a0 + t0a1 + t0^2 a2 + t0^3 a3 + t0^4 a4 + t0^5 a5;
* y(t0) = b0 + t0b1 + t0^2 b2 + t0^3 b3 + t0^4 b4 + t0^5 b5;
* x'(t0) = a1 + 2t0a2 + 3t0^2 a3 + 4t0^3 a4 + 5t0^4 a5;
* y'(t0) = b1 + 2t0b2 + 3t0^2 b3 + 4t0^3 b4 + 5t0^4 b5;
* x''(t0) = 2a0 + 6t0a3 + 12t0^2 a4 + 20t0^3 a5;
* y''(t0) = 2b0 + 6t0b3 + 12t0^2 b4 + 20t0^3 b5;
* x(t1) = a0 + t1a1 + t1^2 a2 + t1^3 a3 + t1^4 a4 + t1^5 a5;
* y(t1) = b0 + t1b1 + t1^2 b2 + t1^3 b3 + t1^4 b4 + t1^5 b5;
* x'(t1) = a1 + 2t1a2 + 3t1^2 a3 + 4t1^3 a4 + 5t1^4 a5;
* y'(t1) = b1 + 2t1b2 + 3t1^2 b3 + 4t1^3 b4 + 5t1^4 b5;
* x''(t1) = 2a0 + 6t1a3 + 12t1^2 a4 + 20t1^3 a5;
* y''(t1) = 2b0 + 6t1b3 + 12t1^2 b4 + 20t1^3 b5;
*
* 共12个方程,其中12个未知数(a0 - a5, b0 - b5),可以通过线性方程组求出唯一解,
* 即:X = A * T,Y = B * T; 求解A、B。
* 注意:五次多项式插值速度曲线并没有匀速段,因此这种规划方式不适用于笛卡尔空间的要求匀速的场合的规划。
*
*/
int main() {
// 初始化图形窗口
pangolin::CreateWindowAndBind("interpolation", Swidth, Sheight);
glEnable(GL_DEPTH_TEST);
// Define Projection and initial ModelView matrix
pangolin::OpenGlRenderState camera(
// 图像宽度、高度、4个内参fx fy cx cy以及最近、最远视距
pangolin::ProjectionMatrix(Swidth, Sheight, 1500, 1500, Swidth/2, Sheight/2, 0.1, 2500),
/*相机的初始坐标,相机视点的初始位置(即相机光轴朝向),相机轴方向*/
pangolin::ModelViewLookAt(0, Sheight/2, 1800, 0, Sheight/2, 0, pangolin::AxisY));
// Create Interactive View in window
pangolin::Handler3D handler(camera);
pangolin::View& view = pangolin::CreateDisplay()
/*底、顶、左、右、显示长宽比//视图在视窗中的范围*/
.SetBounds(0.0, 1.0, 0.0, 1.0, -1.f * Swidth/Sheight)
/*handler绑定渲染状态*/
.SetHandler(&handler);
Polynomial poly;
poly.SetPangolinParams(&camera, &view);
poly.state = DriveStatus::ahead;
while(!pangolin::ShouldQuit()) {
// Clear screen and activate view to render into
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
view.Activate(camera);
// draw the original axis
glLineWidth(3);
glColor3f(0.8f, 0.f, 0.f); // R,G,B
glBegin(GL_LINES);
// x
glVertex3f(0, 0, 0);
glVertex3f(10, 0, 0);
glColor3f(0.f, 0.8f, 0.f);
// y
glVertex3f(0, 0, 0);
glVertex3f(0, 10, 0);
glColor3f(0.2f, 0.2f, 1.f);
// z
glVertex3f(0., 0., 0.);
glVertex3f(0., 0., 10.);
glEnd();
poly.process();
// Swap frames and Process Events
pangolin::FinishFrame();
}
return 0;
}CMakeLists.txt:
# Find Pangolin (https://github.com/stevenlovegrove/Pangolin)
find_package(Pangolin 0.4 REQUIRED)
include_directories(${Pangolin_INCLUDE_DIRS})
add_executable(quintic_polynomial interpolation.cpp)
target_link_libraries(quintic_polynomial ${Pangolin_LIBRARIES})编译步骤:
mkdir build
cd build
cmake ..
make运行步骤:
./quintic_polynomial运行效果
首先是一段车辆先直行、后避障变道、最后再直行的路径规划过程,其中:绿色的线表示模拟车道,上方红色矩形表示前方障碍车辆,下方红色矩形表示自车,黄色虚线表示自车规划路径:
(1)直行:

(2)避障变道

(3)继续直行

最后会同时展示出速度和加速度关于时间变化的曲线(为了方便,没有单独绘制,直接利用Pangolin原界面绘制);同时由于本文程序所用的坐标系与原文中有区别,所以下面的曲线也会有所不同:
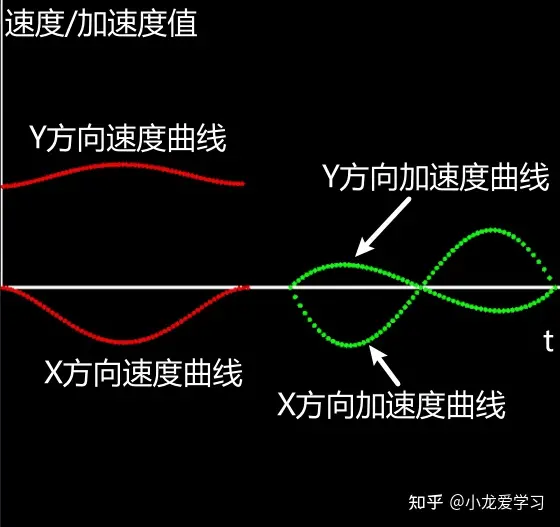
搞定!!!
① 全网独家视频课程
BEV感知、毫米波雷达视觉融合、多传感器标定、多传感器融合、多模态3D目标检测、点云3D目标检测、目标跟踪、Occupancy、cuda与TensorRT模型部署、协同感知、语义分割、自动驾驶仿真、传感器部署、决策规划、轨迹预测等多个方向学习视频(扫码学习)
 视频官网:www.zdjszx.com
视频官网:www.zdjszx.com
② 国内首个自动驾驶学习社区
近2000人的交流社区,涉及30+自动驾驶技术栈学习路线,想要了解更多自动驾驶感知(2D检测、分割、2D/3D车道线、BEV感知、3D目标检测、Occupancy、多传感器融合、多传感器标定、目标跟踪、光流估计)、自动驾驶定位建图(SLAM、高精地图、局部在线地图)、自动驾驶规划控制/轨迹预测等领域技术方案、AI模型部署落地实战、行业动态、岗位发布,欢迎扫描下方二维码,加入自动驾驶之心知识星球,这是一个真正有干货的地方,与领域大佬交流入门、学习、工作、跳槽上的各类难题,日常分享论文+代码+视频,期待交流!

③【自动驾驶之心】技术交流群
自动驾驶之心是首个自动驾驶开发者社区,聚焦目标检测、语义分割、全景分割、实例分割、关键点检测、车道线、目标跟踪、3D目标检测、BEV感知、多模态感知、Occupancy、多传感器融合、transformer、大模型、点云处理、端到端自动驾驶、SLAM、光流估计、深度估计、轨迹预测、高精地图、NeRF、规划控制、模型部署落地、自动驾驶仿真测试、产品经理、硬件配置、AI求职交流等方向。扫码添加汽车人助理微信邀请入群,备注:学校/公司+方向+昵称(快速入群方式)

④【自动驾驶之心】平台矩阵,欢迎联系我们!
























 3万+
3万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








