MMA-利用Methematica推导一阶线性微分方程

Methematica是一款符号运算的利器，可以完成各种复杂的符号运算。在这里我们尝试利用这一软件进行一阶微分方程的推导。首先回顾一下一阶微分方程的解法。

一阶线性微分方程

齐次方程通解

首先将非齐次方程存储到一个名为“非齐次方程”的符号中，然后求解相应齐次方程的通解并存储在“齐次方程通解”中。

DSolve[D[y[x], x] + p[x] y[x] == q[x], y[x], x]
(*即可获得非齐次方程的通解： *)
非齐次方程 = HoldForm[D[y[x], x] + p[x] y[x] == q[x]]
(*将非齐次方程存储到一个名为“非齐次方程”的符号中*)
齐次方程通解 = DSolve[D[y[x], x] + u[x] y[x] == 0, y[x], x]
(*求解相应齐次方程的通解并存储在“齐次方程通解”*)

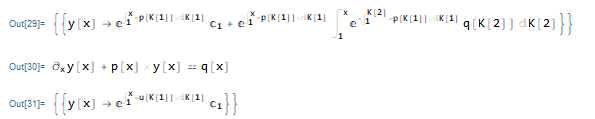
非齐次方程的通：

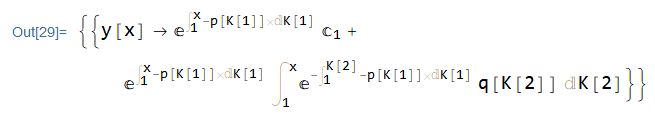
非齐次方程通解

利用常数变易法。
常数变易法是解线性微分方程行之有效的一种方法。它是拉格朗日十一年的研究成果，我们所用仅是他的结论，并无过程。
常数变易法是个特殊的变量代换法。

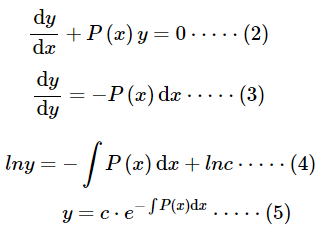
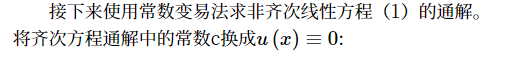
常数变易方程 = 齐次方程通解 /. C[1] -> C[1][x]
(*将通解中的常数项c1替换为C[x]并存储在“常数变易方程”中*)

非齐次方程 = HoldForm[D[y[x], x] + p[x] y[x] == q[x]]
(*将非齐次方程存储到一个名为“非齐次方程”的符号中*)

常数方程 = ReleaseHold[非齐次方程 /. 常数变易方程]
(*将变易后的方程代到非齐次方程中，可以得到含有常数函数的方程*)
常数解 = DSolve[常数方程, C[1], x]
(**)
特解 = 齐次方程通解 /. C[1] -> C[1][x] /. 常数解
(*使用常数函数替换齐次方程通解中的常数，可得特解*)
非齐次通解 = y[x] -> Simplify[((y[x] /. 特解) + (y[x] /. 齐次方程通解))]
(*非齐次方程的通解为特解+齐次通解：*)
ReleaseHold[非齐次方程 /. 非齐次通解]
(*验证一下，将非齐次通解带入原来的非齐次方程检验是否正确*)

常数变易方程：

接下来，将通解中的常数项c1替换为C[x]并存储在“常数变易方程”中：
将变易后的方程代到非齐次方程中，可以得到含有常数函数的方程：
使用常数函数替换齐次方程通解中的常数，可得特解：

1、将通解中的常数项c1替换为C[x]并存储在“常数变易方程”中*

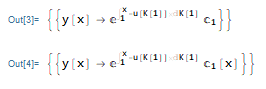
2、将变易后的方程代到非齐次方程中，可以得到含有常数函数的方程：

附录

齐次方程通解 = DSolve[D[y[x], x] + u[x] y[x] == 0, y[x], x]
常数变易方程 = 齐次方程通解 /. C[1] -> C[1][x]
常数方程 = ReleaseHold[非齐次方程 /. 常数变易方程]
常数解 = DSolve[常数方程, C[1], x]
特解 = 齐次方程通解 /. C[1] -> C[1][x] /. 常数解
非齐次通解 = y[x] -> Simplify[((y[x] /. 特解) + (y[x] /. 齐次方程通解))]
ReleaseHold[非齐次方程 /. 非齐次通解]