模电 - 半导体二极管

最新推荐文章于 2024-02-22 18:33:13 发布

江南小作坊

最新推荐文章于 2024-02-22 18:33:13 发布

阅读量2k

点赞数 2

分类专栏：模拟与数字电路

本文链接：https://blog.csdn.net/Cherish1ove/article/details/113796448

版权

模拟与数字电路专栏收录该内容

15 篇文章

订阅专栏

本文详细介绍了半导体二极管的结构、伏安特性、温度影响、主要参数和等效电路模型。讨论了二极管在整流、限幅、钳位和开关电路中的应用，并分析了其工作原理。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

半导体二极管

常见结构

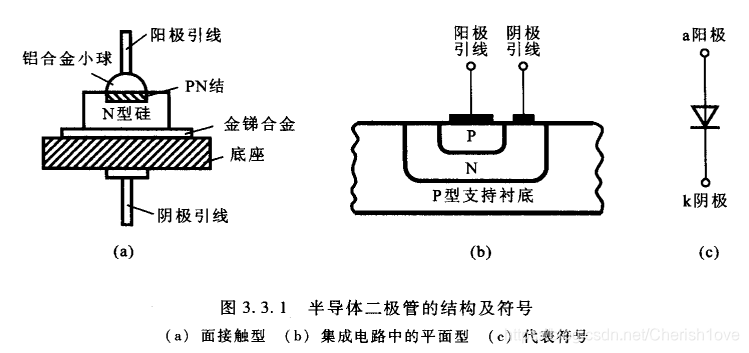
在这里插入图片描述

与PN结对比

存在体电阻，电流比PN结电流小
反向电流大一些（封装外壳存在漏电）

伏安特性

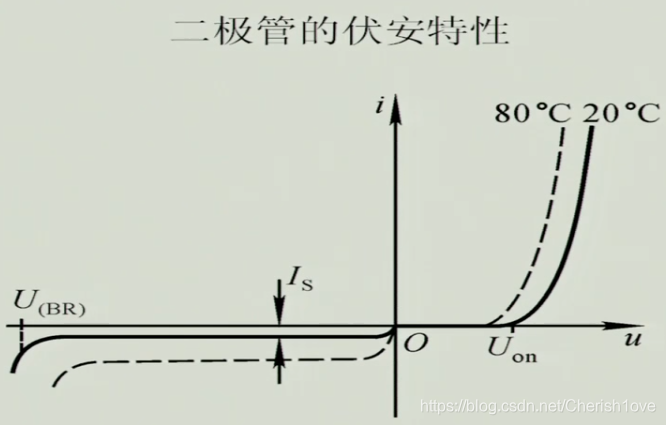
在这里插入图片描述

温度对其影响

温度上升，正向导通伏安曲线左移，反向饱和电流下移。
室温下，每升高1℃，正向电压下降2-2.5mV；每升高10℃，反向饱和电流增大一倍。

二极管的主要参数

门坎电压（死区电压）：V_th，正向导通时，类似一个和大电阻，好像有个门坎。硅管V_th约为0.5V，锗管V_th约为0.1V。由于二极管导通后，曲线较垂直陡峭，通常认为，硅管正向导通压降约为0.7V，锗管约为0.2V。
最大整流电流：I_F，二极管正向通过电流平均值的最大值–工作时能承受的功率最大值对应的电流。
反向击穿电压：V_BR，管子反向击穿时的电压值，一般手册上给出的最高反向工作电压约为击穿电压的50%：
反向电流：I_R，指管子未击穿时的反向电流，其值越小，管子的单向导电性越好。
极间电容：C_d，PN结存在扩散电容C_D和势垒电容C_B，极间电容就是反映二极管中PN结电容效应的参数，Cd= C_D+C_B。
最高工作频率（上限频率）：f_M：由于PN结上面的极间电容，如果工作频率大，电容近似短路，破坏单向导电性。在高频电路中要注意这个。
反向恢复时间：T_RR：当二极管外加电压极性翻转时，其原工作状态不能在瞬间完全随之变化。特别是外加电压从正向偏置变成反向偏置时，二极管中电流由正向变为反向，但其翻转后瞬间有较大的反向电流，经过一定的时间后反向电流才会变得很小。如下图：二极管由正向导通到反向截止时电流的变化。

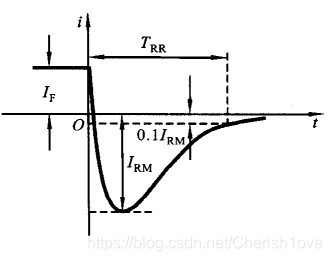
存在反向恢复时间是因为扩散电容的影响，扩散电容越小，反向恢复时间越短，工作频率越高。

在这里插入图片描述

二极管等效电路模型

理想模型
恒压降模型与折线模型
小信号模型（小信号分析法）
- 当输入信号是一个小信号的时候，远没有达到二极管的导通压降，仅仅只有小信号的激励无法穿过二极管，这时就可以加入一个直流电压源，使得二极管工作在合适的静态工作点（Q），从而将小信号传输过来（此处的思想模型对三极管的工作原理有很大的启发）。当v_s=V_msin(wt)时（V_m<<V_DD）,电路的负载线为： $i_D=-\frac{1}{R}v_{D}+\frac{1}{R}(V_{DD}+v_{s})$
- 把二极管的伏安曲线以Q点为切点的一条直线，如下图，其斜率的倒数就是小信号模型的微变电阻r_d，其模型如下：
- 微变电阻： $r_{d} =\Delta v_{D}/\Delta i_{D}$
- 二极管的指数模型： $i_{D}=I_{s}(e^{\frac{v}{V_{T}}}-1)$
- 微变电导： $g_{d}=\frac{1}{r_{d}}=\frac{di_{D}}{dv_{D}}=\frac{\mathrm{d} [I_{s}(e^{v_{D}/{V_{T}}}-1)]}{\mathrm{d} v_{D}}=\frac{I_{s}}{V_{T}}e^{v_{D}/{V_{T}}}$
- 在Q点处： $v_{D}>>V_{T}=26mV，i_{D}\approx I_{s}e^{v_{D}/V_{T}}$
- 原式等于： $g_{d}=\frac{I_{s}}{V_{T}}e^{v_{D}/{V_{T}}}\approx \frac{I_{D}}{V_{T}}$
- 由此可得： $r_{d}=\frac{1}{g_{d}}=\frac{V_{T}}{I_{D}}=\frac{26(mV)}{I_{D}{(mA)}},(常温下，T=300K)$
- 如上图3.4.5，对整个电路进行分析：总电流=直流+交流
  - 直流部分： $I_{D}=\frac{V_{DD}-v_{D}}{R}$
  - 交流部分： $i_{d}=\frac{U_{s}}{r_{d}+R}$
  - 总电流： $i_{D} = i_{d}+I_{D}$
  - 高频电路模型：

二极管的基本电路及分析

整流电路：所谓整流通常是指双极性电压（或电流）变为单极性电压（或电流）处理过程。如下图：半波整流电路。
**
**：在电子电路中，常用限幅电路对各种信号进行处理。它用来让信号在预置的电平范围内有选择地传输一部分。限幅电路有时也称为削波电路。利用二极管的正向导通曲线（利用正向导通的稳压作用）。
钳位电路：可以在完整信号波形中叠加一个直流电平，通常要配合电容器使用。设二极管导通压降V_D=0.7V，v_s=V_msinwt V，且V_m>>V_D，稳态出v_o的波形如下图：
只有在v_s的负半周，D才有可能导通，此时电容器充电，充电的最高电压为V_C=V_m-V_D=V_m-0.7 V。由于D导通时，整个回路的电阻非常小，所以电容器C上的电压可以快速充至最大值。但是电容C并无放电回路，所以充电完毕后，C上的电压V_C始终保持不变，此后电路进入稳态。这时输出电压为 $v_{o}=v_{s}+V_{c}=v_{s}+V_{m}-0.7 (V)$ 若二极管方向颠倒，输出波形相当于输入波形的顶部钳位在+0.7V的直流电平上。所以，钳位电路的作用可以看作是将周期性变化的波形的顶部/底部保持在某一确定的直流电平上。
开关电路：利用二极管的单向导电性可以接通或断开电路。数字电路广泛应用。
- 分析过程：
  - 假设二极管处于截止状态（理想模型v_D<0；恒压降模型v_D<V_D，均有i_D=0），二极管相当于开路；
  - 求出v_D的值；
  - 若v_D<=0，则说明假设成立，二极管实际处于截止状态，所得结果即为所求，若v_D>0，则表明假设错误，二极管实际处于导通状态，再根据导通状态重新求解电路。
    先假设两二极管均截止（断开），4.7kΩ电阻中无电流流过，两二极管阳极电位为5 V。当v₁₁=0 V、v₁₂=5 V，得v_D1=5 V > 0，v_D2=0，表明D₁的假设错误，实际上是正向偏置，所以D₁导通；D₂的偏置电压为0 V，假设成立，即D₂截止。D₁导通时，v_o=0V，此时D₂的阴极电位为5V，阳极为0V，仍为截止状态。分析结果如下：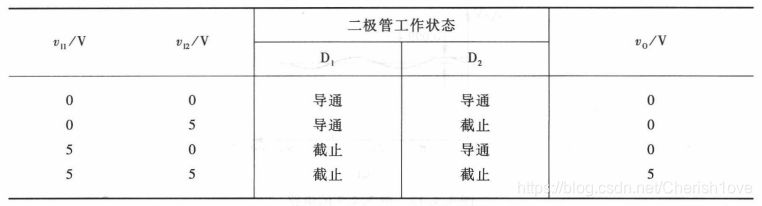
    只要有一个为0V，则输出为0V；只有当两个输入电压为5V，输出才为5V，与逻辑。
小信号：微变电阻r_d是与静态工作点Q有关的，这个分析方法类似叠加原理。即先分析直流通路，再分析交流通路，最有叠加。要注意的是：分析静态与动态的二极管的模型不同。
- 分析方法：
  - 1.分析电路的静态工作点，求得静态工作点Q；
  - 2.根据静态工作点Q算出微变电阻r_d；
  - 3.根据小信号模型的交流等效电路，求出小信号作用下电路的交流电压、电流；
  - 4.与静态值叠加，得到电路响应的总量结果。
- 如下图：V_DD=5V，R=5kΩ，恒压降模型的V_D=0.7V，信号源v_s=0.1sinwt。
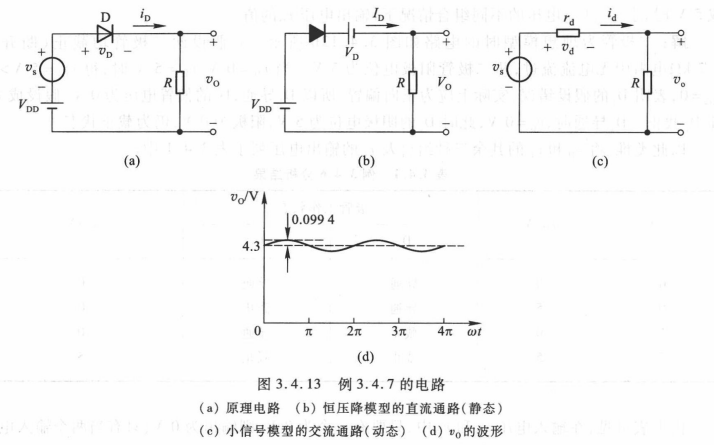
- 将两个电压源V_DD与v_s分开考虑，得到相应的等效电路
- 静态工作点： $V_{D}=0.7V$ $I_{D}=(V_{DD}-V_{D})/R=(5-0.7)V/5kΩ=0.86 mA$ 输出电压的直流分量为： $V_{o}=I_{D}R=0.86mA*5kΩ=4.3V$
- 此静态工作点下的微变电阻： $r_{d}=\frac{V_{T}}{I_{D}}=\frac{26mV}{0.86mA}\approx30Ω=0.03kΩ$
- 输出电压交流分量： $v_{o}=\frac{R}{r_{d}+R}*v_{s}=\frac{5kΩ}{5kΩ+0.03kΩ} *0.1sinwt\approx0.0994sinwt(V)$
- 输出电压总量： $v_{O}=V_{o}+v_{o}=(4.3+0.0994sinwt)V$
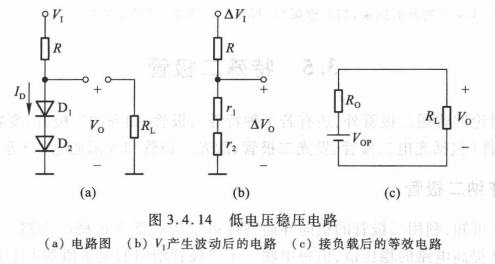
低电压稳压电路：利用二极管的正向导通特性，可以获得一种稳压性能较好的低电压稳压电路。二极管小信号模型可以用于此种电路稳压特性的分析。