Unity中的数学基础——向量

一：概念 

——向量也称为矢量，是具有大小和方向的量(零向量比较特殊，是唯一一个大小为0并且没有方向的向量)。向量的大小(长度)称为模，长度为1的向量称为单位向量
——书写向量时，水平书写的向量([1,2,3])叫做行向量，垂直书写的向量叫做列向量

---

二：点与向量的关系

点代表了一个位置，他没有大小和方向的概念。而向量具有大小和方向的概念。Unity中的transform.position代表了一个点，它不具有方向。transform.forward代表了一个向量，它代表了当前物体在世界坐标z轴上的指向。但是他们在Unity中都是通过(x,y,z)来表示的

---

三：向量的几种关系

——向量AB不等于向量BA，因为方向不同
——向量AB等于负的向量BA，因为方向相同
——向量AB的长度等于向量BA的长度
——向量AB+向量BA=零向量，因为两个向量相反

---

四：单位向量

长度为1的向量称为单位向量。当我们只关心向量方向，不关心向量大小时，则可以使用单位向量。 
普通向量变换为单位向量的过程称为向量归一化

Vector3 A = new Vector3(1, 2, 3);
Vector3 B = new Vector3(2, 4, 5);

Vector3 v = (B - A).normalized;
Debug.Log("AB向量归一化后的坐标：" + v);    //AB向量归一化后的坐标：(1/3,2/3,2/3)

---

五：向量的长度

Vector3 A = new Vector3(1, 2, 3);
Vector3 B = new Vector3(2, 4, 5);

//第一种方法：Vector3.Magnitude，Vector3.SqrMagnitude求出的是长度的平方
float dis = Vector3.Magnitude(B - A);

//第二种方法：Vector3.Distance
//float dis = Vector3.Distance(A, B);

Debug.Log("AB向量的长度：" + dis);    //AB向量的长度：3

---

六：向量的点积(内积)

几何意义：一条边向另一条边的投影长度乘以另一条边的长度

向量点积后的结果是一个标量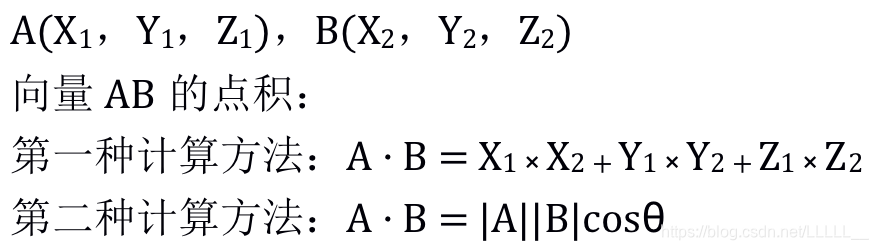

点乘的结果大于0，则两个向量的夹角0<=θ<90
点乘的结果等于0，则两个向量的夹角θ=90，互相垂直
点乘的结果小于0，则两个向量的夹角90<θ<=180

Vector3 A = new Vector3(1, 1);
Vector3 B = new Vector3(1, 0);

float dot = Vector3.Dot(A, B);
Debug.Log("A向量与B向量的点乘为：" + dot);    //A向量与B向量的点乘为：1

---

七：向量的叉积(外积)

几何意义：结果是一个与这两个向量都垂直的向量，结果的模长是以两个向量为边的平行四边形的面积

以下结论都是以左手定则为准的：（二维向量比较叉积的Z值，三维向量比较叉积的Y值）
叉乘的结果大于0，则向量A旋转到向量B是顺时针
叉乘的结果等于0，则向量A与向量B是共线的
叉乘的结果小于0，则向量A旋转到向量B是逆时针

Vector3 A = new Vector3(1, 2, 3);
Vector3 B = new Vector3(-2, -2, 3);

Vector3 cross = Vector3.Cross(A, B);
Debug.Log("A向量与B向量的叉乘为：" + cross);    //A向量与B向量的叉乘为：(12,-9,2)

---

八：求一个向量在另一个向量上的投影以及投影长度

求一个向量在另一个向量上的投影长度以及投影：

Vector3 projection = Vector3.Project(new Vector3(4, 4, 4), new Vector3(0, 0, 1));
float projectionDis = projection.magnitude;

Debug.Log("向量(4,4,4)在向量(0,0,1)上的投影向量为：" + projection);
Debug.Log("向量(4,4,4)在向量(0,0,1)上的投影长度为：" + projectionDis);

---

九：向量在游戏中的运用案例

——使用点乘求敌人在玩家的前后

using System;
using UnityEngine;

public class Test : MonoBehaviour
{
    public GameObject player;
    public GameObject enemy;

    private void Update()
    {
        Vector3 v1 = enemy.transform.position - player.transform.position;
        Vector3 v2 = player.transform.forward;
        float dot = Vector3.Dot(v1, v2);
        if (dot > 0)
        {
            Debug.Log("敌人在前方");
        }
        else if (dot < 0)
        {
            Debug.Log("敌人在后方");
        }
        else
        {
            Debug.Log("敌人在正左右方向");
        }
    }
}

——使用点乘求两个向量的角度
与Vector3.Angle求出的结果相同
因为A*B=|A|*|B|*cos<a,b>，所以可以算出来两个向量的单位向量，单位向量长度为1，然后用反余弦arccos求A和B向量的夹角

using System;
using UnityEngine;

public class Test : MonoBehaviour
{
    private float GetAngle(Vector3 a, Vector3 b)
    {
        Vector3 v1 = a.normalized;
        Vector3 v2 = b.normalized;
        float v3 = Vector3.Dot(v1, v2);
        float angle = Mathf.Acos(v3) * Mathf.Rad2Deg;
        return angle;
    }
}

——求一个向量到另一个向量的夹角，带方向
与Vector3.SignedAngle求出的结果相同

private void GetAngle(Vector3 a, Vector3 b)
{
    Vector3 c = Vector3.Cross(a, b);
    float angle = Vector3.Angle(a, b);

    float sign = Mathf.Sign(Vector3.Dot(c.normalized, Vector3.Cross(a.normalized, b.normalized)));
    float signed_angle = angle * sign;
    Debug.Log("a -> b :" + signed_angle);

    sign = Mathf.Sign(Vector3.Dot(c.normalized, Vector3.Cross(b.normalized, a.normalized)));
    signed_angle = angle * sign;
    Debug.Log("b -> a :" + signed_angle);
}

Vector3.Angle求得的是不带符号的角度，在0度到180度之间
Vector2.SignedAngle求得的是带符号的角度，向量a到向量b是逆时针，结果是正数，反之，结果是负数，如果是180度则都是正数180，Vector3.SignedAngle与Vector2.SignedAngle结果相反，正数是顺时针

——使用叉乘求敌人在玩家的左右 

using UnityEngine;

public class Test : MonoBehaviour
{
    public GameObject player;
    public GameObject enemy;

    private void Update()
    {
        Vector3 v1 = player.transform.forward;
        Vector3 v2 = enemy.transform.position - player.transform.position;
        Vector3 cross = Vector3.Cross(v1, v2);
        if (cross.y > 0)
        {
            Debug.Log("敌人在右边");
        }
        else if (cross.y < 0)
        {
            Debug.Log("敌人在左边");
        }
        else
        {
            Debug.Log("敌人与玩家方向相同");
        }
    }
}

——使用叉乘求两个向量的角度（基本上不会用到）
因为|A*B|=|A|*|B|*sin<a,b>，所以可以用反余弦arcsin求A和B向量的夹角

using System;
using UnityEngine;

public class Test : MonoBehaviour
{
    private float GetAngle(Vector3 a, Vector3 b)
    {
        float v3 = Vector3.Distance(Vector3.zero, Vector3.Cross(a.normalized, b.normalized));
        float angle = Mathf.Asin(v3) * Mathf.Rad2Deg;
        return angle;
    }
}

---

十：向量的一些公式

——已知向量a(x1,y1)与向量b(x2,y2)垂直，x1*x2+y1*y2=0
——已知向量a(x1,y1)，则向量a的方向为y1/x1
——已知向量a的斜率为k，向量b与向量a垂直，则向量b的斜率为-1/k