CNN模型的计算量、参数、显存占用

经典CNN模型的计算量、参数、显存占用

1. 深度学习复杂度

通常用Forward Pass计算量和参数个数(#Parameters)来描述复杂度 ,因为模型的部署需要考虑网络参数的大小和计算力.

对网上一些很好的讲解做一个总结.

2. FLOPS概念

Floating point operations 浮点运算数量

Paper里比较流行的单位是GFLOPs

1 GFLOPs = 10^9 FLOPs

即：10亿次浮点运算

MAC: 一次乘法和加法运算

Image大小为 5x5 ,卷积核大小为3×3, 假设channel为1

FLOPs:那么一次3x3的卷积（求右图矩阵一个元素的值）所需运算量：(3x3)个乘法+(3x3-1)个加法 = 17 , 要得到右图convolved feature （3x3的大小）：17x9 = 153

Params: 1×(3×3+1) = 10(后面有详细的参数量计算方法讲解)

\

3.参数量计算

参数量的计算主要在卷积层参数量的计算和全连接层参数量计算,在[qian99][ https://blog.csdn.net/qian99/article/details/79008053 ]的博客中讲解的非常详细,上面公式也提供了卷积层的计算方法, 至于全连接层, 举个例子nn.Linear(2048, 101),, 这个全连接层的参数量为2048×101+101(也有说这里是1,参考qian99博客).

4. 输出特征图尺寸

最后记录一下卷积输出大小:N = (W − F + 2P )/S+1其中N为卷积输出N×N, 输入图片大小 W×W , Filter大小 F×F , 步长 S, padding的像素数 P .

池化层:和卷积层计算类似. 注意池化层没有参数! 通过我们后面的网络模型也可以看出来. 池化层的卷积核的参数已经被人为设定，例如2*2的平均池化的参数被设为[0.25,0.25;0.25,0.25]

计算尺寸不被整除只在GoogLeNet中遇到过。卷积向下取整，池化向上取整.

三种不同模式是对卷积核移动范围的不同限制。

1. full mode

   

   橙色部分为image, 蓝色部分为filter。full模式的意思是，从filter和image刚相交开始做卷积，白色部分为填0。filter的运动范围如图所示。

2. same mode

   

   当filter的中心(K)与image的边角重合时，开始做卷积运算，可见filter的运动范围比full模式小了一圈。注意：这里的same还有一个意思，卷积之后输出的feature map尺寸保持不变(相对于输入图片)。当然，same模式不代表完全输入输出尺寸一样，也跟卷积核的步长有关系。same模式也是最常见的模式，因为这种模式可以在前向传播的过程中让特征图的大小保持不变，调参师不需要精准计算其尺寸变化(因为尺寸根本就没变化)。

3. valid

   

   当filter全部在image里面的时候，进行卷积运算，可见filter的移动范围较same更小了。

   输出特征图的计算万变不离其宗, 掌握计算公式, 例如我们需要same模式, 使输出特征图和输入特征图的尺寸相同, 这样带入我们的N = (W − F + 2P )/S+1公式N=W, S=1, F卷积核也确定, 这样我们就可以确定padding了.

5. 常用模型的FlOPs和参数量

使用torchsummary或者**pytorch-OpCounter**都是很好用的计算模型大小的工具. qian99的博客中讲的很详细.

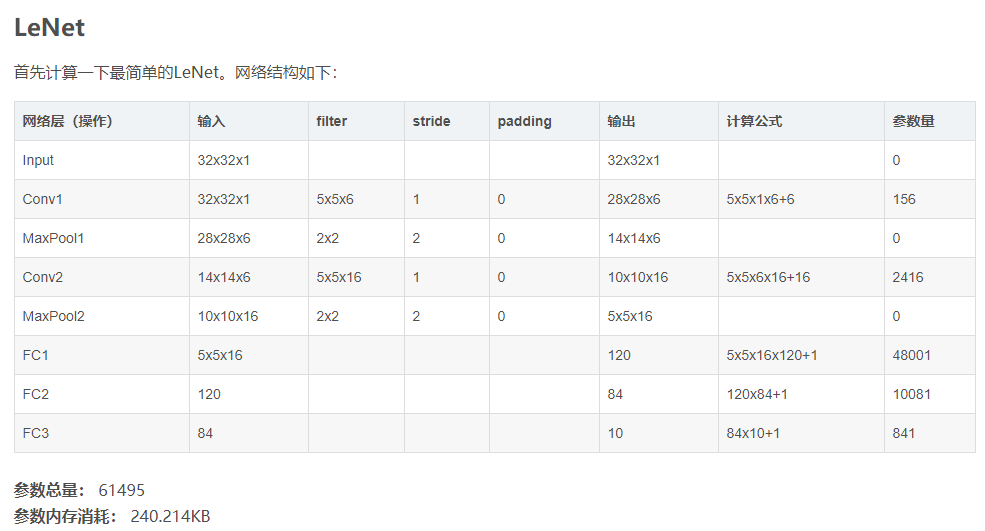
使用torchsummary和OpCounter:

6. 参数量和占用GPU显存的关系

本节主要转载 Oldpan的个人博客
浅谈深度学习:如何计算模型以及中间变量的显存占用大小（https://oldpan.me/archives/how-to-calculate-gpu-memory）

显卡炸了…

torch.FatalError: cuda runtime error (2) : out of memory

显然是显存装不下你那么多的模型权重还有中间变量，然后程序奔溃了。 这里的模型权重指的就是我们上面计算的参数量大小, 中间变量指的是我们计算forword和bacword时需要保存的中间变量. 通过上面的torchsummary截图可以看到, 中间变量占了很大的显存. 怎么办，其实办法有很多，及时清空中间变量，优化代码，减少batch，等等等等，都能够减少显存溢出的风险。

1.基础知识：

• 1 G = 1000 MB
• 1 M = 1000 KB
• 1 K = 1000 Byte
• 1 B = 8 bit

然后我们说一下我们平常使用的向量所占的空间大小，以Pytorch官方的数据格式为例（所有的深度学习框架数据格式都遵循同一个标准）：

我们只需要看左边的信息，在平常的训练中，我们经常使用的一般是这两种类型：

• float32 单精度浮点型
• int32 整型

一般一个8-bit的整型变量所占的空间为1B也就是8bit。而32位的float则占4B也就是32bit。而双精度浮点型double和长整型long在平常的训练中我们一般不会使用。

也就是说，假设有一幅RGB三通道真彩色图片，长宽分别为500 x 500，数据类型为单精度浮点型，那么这张图所占的显存的大小为：500 x 500 x 3 x 4B = 3M。

先看看输入图片所占用的显存。训练网络首先就是加载训练图像，例如一个 (256,3,100,100)-(N,C,H,W)的FloatTensor所占的空间为256×3×100×100=31M

可以看到输入的训练图像和网络模型的参数所占的显存并不是很大，那么显存去哪了？

2. 显存去哪了

占用显存比较多空间的并不是我们输入图像，而是神经网络中的中间变量以及使用optimizer算法时产生的巨量的中间参数。

我们首先来简单计算一下Vgg16这个net需要占用的显存：

通常一个模型占用的显存也就是两部分：

• 模型自身的参数(params)
• 模型计算产生的中间变量(memory)

图片来自cs231n，这是一个典型的sequential-net，自上而下很顺畅，我们可以看到我们输入的是一张224x224x3的三通道图像，可以看到一张图像只占用150x4k，但上面标注的是150k，这是因为上图中在计算的时候默认的数据格式是8-bit而不是32-bit，所以最后的结果要乘上一个4。

我们可以看到，左边的memory值代表：图像输入进去，图片以及所产生的中间卷积层所占的空间。我们都知道，这些形形色色的深层卷积层也就是深度神经网络进行“思考”的过程 。

图片从3通道变为64 –> 128 –> 256 –> 512 …. 这些都是卷积层，而我们的显存也主要是他们占用了。

还有上面右边的params，这些是神经网络的权重大小，可以看到第一层卷积是3×3，而输入图像的通道是3，输出通道是64，所以很显然，第一个卷积层权重所占的空间是 (3 x 3 x 3) x 64。

另外还有一个需要注意的是中间变量在backward的时候会翻倍！

为什么，举个例子，下面是一个计算图，输入x，经过中间结果z，然后得到最终变量L：

我们在forward的时候需要保存下来的中间值。输出是L，然后输入x，我们在backward的时候要求L对x的梯度，这个时候就需要在计算链L和x中间的z：

$\frac{\partial L}{\partial \mathbf{x}}={\left(\frac{\mathrm{d}\mathbf{z}}{\mathrm{d}\mathbf{x}}\right)}^{\mathrm{T}}\frac{\partial L}{\partial \mathbf{z}}\left[{\mathbb{R}}^{A\times 1}={\mathbb{R}}^{A\times B}{\mathbb{R}}^{B\times 1}\right]$

dz/dx这个中间值当然要保留下来以用于计算，所以粗略估计，backward的时候中间变量的占用了是forward的两倍！

3. 优化器和动量

要注意，优化器也会占用我们的显存！

为什么,看这个式子: $W_{t+1}=W_t-\alpha \nabla F\left(W_t\right)$

上式是典型的SGD随机下降法的总体公式，权重W在进行更新的时候，会产生保存中间变量$\nabla F(W)$，也就是在优化的时候，模型中的params参数所占用的显存量会翻倍。

当然这只是SGD优化器，其他复杂的优化器如果在计算时需要的中间变量多的时候，就会占用更多的内存。

4. 模型中各层对显存的占用

有参数的层即会占用显存的层。我们一般的卷积层都会占用显存，而我们经常使用的激活层Relu没有参数就不会占用了。

占用显存的层一般是：

• 卷积层，通常的conv2d
• 全连接层，也就是Linear层
• BatchNorm层
• Embedding层

而不占用显存的则是：

• 刚才说到的激活层Relu等
• 池化层
• Dropout层

具体计算方式：

• Conv2d(Cin, Cout, K): 参数数目：Cin × Cout × K × K
• Linear(M->N): 参数数目：M×N
• BatchNorm(N): 参数数目： 2N
• Embedding(N,W): 参数数目： N × W

5. 额外的显存

总结一下，我们在总体的训练中，占用显存大概分以下几类：

• 模型中的参数(卷积层或其他有参数的层)
• 模型在计算时产生的中间参数(也就是输入图像在计算时每一层产生的输入和输出)
• backward的时候产生的额外的中间参数
• 优化器在优化时产生的额外的模型参数

但其实，我们占用的显存空间为什么比我们理论计算的还要大，原因大概是因为深度学习框架一些额外的开销吧，不过如果通过上面公式，理论计算出来的显存和实际不会差太多的。

6.如何优化

优化除了算法层的优化，最基本的优化无非也就一下几点：

• 减少输入图像的尺寸
• 减少batch，减少每次的输入图像数量（这个经常用）
• 多使用下采样，池化层
• 一些神经网络层可以进行小优化，利用relu层中设置inplace
• 购买显存更大的显卡
• 从深度学习框架上面进行优化
• 补充一下全连接层的设置过大会产生过多的参数和占用过高的显存
• Densenet模型非常不错，可以借鉴。有的时候过多的参数和深度针对规模不大的数据库反而是一种负担，容易造成过拟合。后续我也会针对过拟合有相应的总结。

Oldpan同样有针对pytorch显存的优化博客，等我拜读后再更新。

7.参考引用

[1] CNN 模型所需的计算力（flops）和参数（parameters）数量是怎么计算的？ - 留德华叫兽的回答 - 知乎 https://www.zhihu.com/question/65305385/answer/641705098

[2] CNN 模型所需的计算力（flops）和参数（parameters）数量是怎么计算的？ - 李珂的回答 - 知乎 https://www.zhihu.com/question/65305385/answer/256845252

[3] CNN 模型所需的计算力（flops）和参数（parameters）数量是怎么计算的？ - chen liu的回答 - 知乎 https://www.zhihu.com/question/65305385/answer/451060549

[4] qian99CSDN博客 https://blog.csdn.net/qian99/article/details/79008053 关于参数量讲解非常细致

[5] Lyken17/pytorch-OpCounter github pytorch实现flops和参数量计算

[6] sksq96/pytorch-summary pytorch模型参数

[7] 木盏CSND博客https://blog.csdn.net/leviopku/article/details/80327478

[8] wolf_ray CSDNhttps://oldpan.me/archives/how-to-calculate-gpu-memory

[9] Oldpan的个人博客
96/pytorch-summary)** pytorch模型参数

[7] 木盏CSND博客https://blog.csdn.net/leviopku/article/details/80327478

[8] wolf_ray CSDNhttps://oldpan.me/archives/how-to-calculate-gpu-memory

[9] Oldpan的个人博客
浅谈深度学习:如何计算模型以及中间变量的显存占用大小（https://oldpan.me/archives/how-to-calculate-gpu-memory） 非常棒极力推荐去学习！