梯度下降、牛顿法、高斯牛顿&L-M算法比较

最新推荐文章于 2024-11-21 15:05:58 发布

OORRANNGGE

最新推荐文章于 2024-11-21 15:05:58 发布

阅读量9k

点赞数 9

分类专栏：数值优化

本文链接：https://blog.csdn.net/OORRANNGGE/article/details/90696602

版权

本文对比了四种优化算法：梯度下降法、牛顿法、高斯-牛顿法和L-M算法。一阶方法的梯度下降法虽然简单，但收敛速度较慢；二阶方法如牛顿法收敛速度快，但计算Hessian矩阵复杂；高斯-牛顿法简化了计算，但可能在某些情况下收敛变慢；L-M算法结合了梯度下降和高斯-牛顿的优点，通过调整λ参数提高了鲁棒性。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

本文梳理一下常见的几种优化算法：梯度下降法，牛顿法、高斯-牛顿法和L-M算法，优化算法根据阶次可以分为一阶方法（梯度下降法），和二阶方法（牛顿法等等），不同优化算法的收敛速度，鲁棒性都有所不同。一般来讲，二阶方法要比一阶方法有更快的收敛速度。

梯度下降法

梯度下降法是一种简洁直观的寻找极小值的迭代算法，它总是沿着负梯度方向进行搜索，直到梯度为0才收敛。它的迭代公式为：
$\bm x_{k+1} = \bm x_k - \alpha f'(\bm x_k)$
其中 $\alpha$ 为搜索步长，是一个需要人为给定的值，当然你也可以设计一种自适应的给定 $\alpha$ 的算法。 $\alpha$ 的选择会影响梯度下降法的收敛速度。下图是从(1,1)出发在 $f(x)=x^2$ 上寻找最小值点的搜索路径。

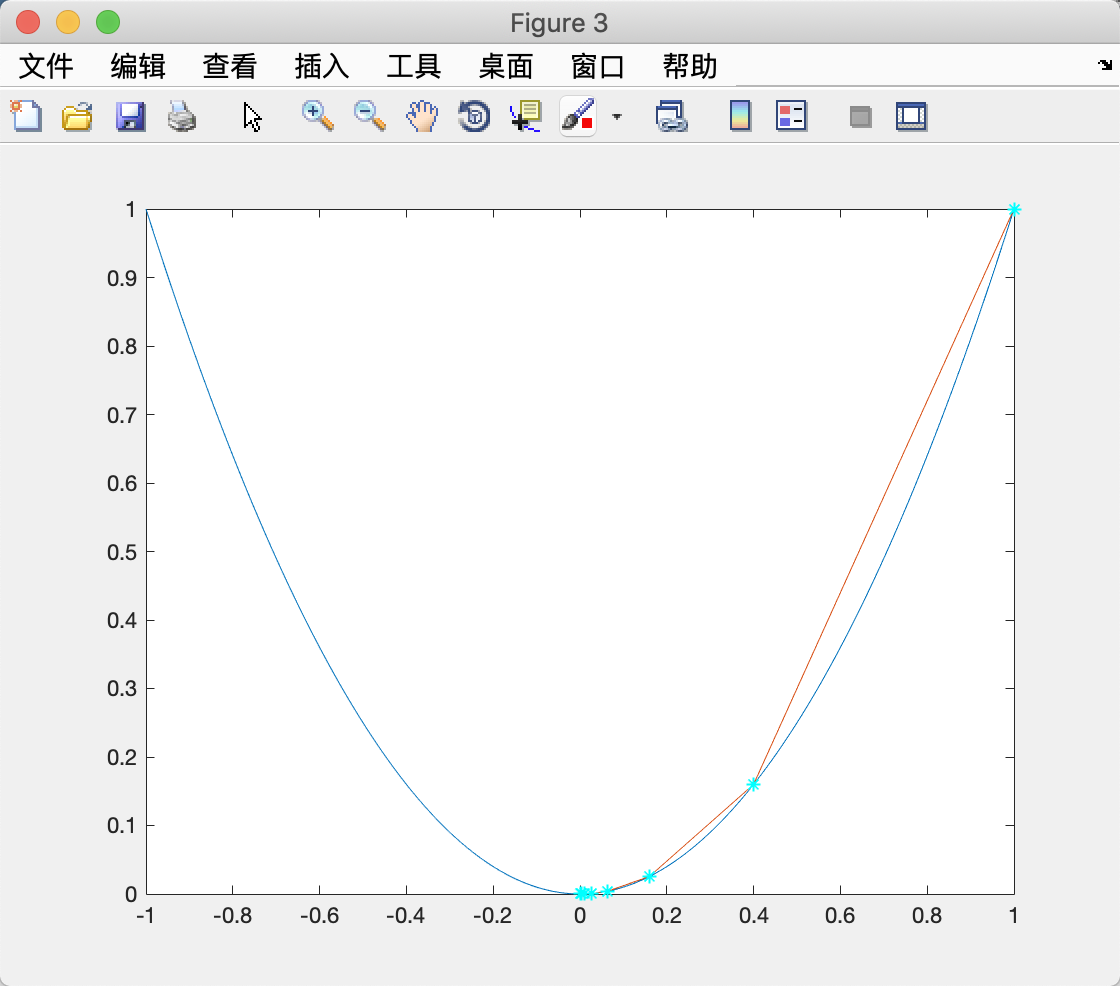
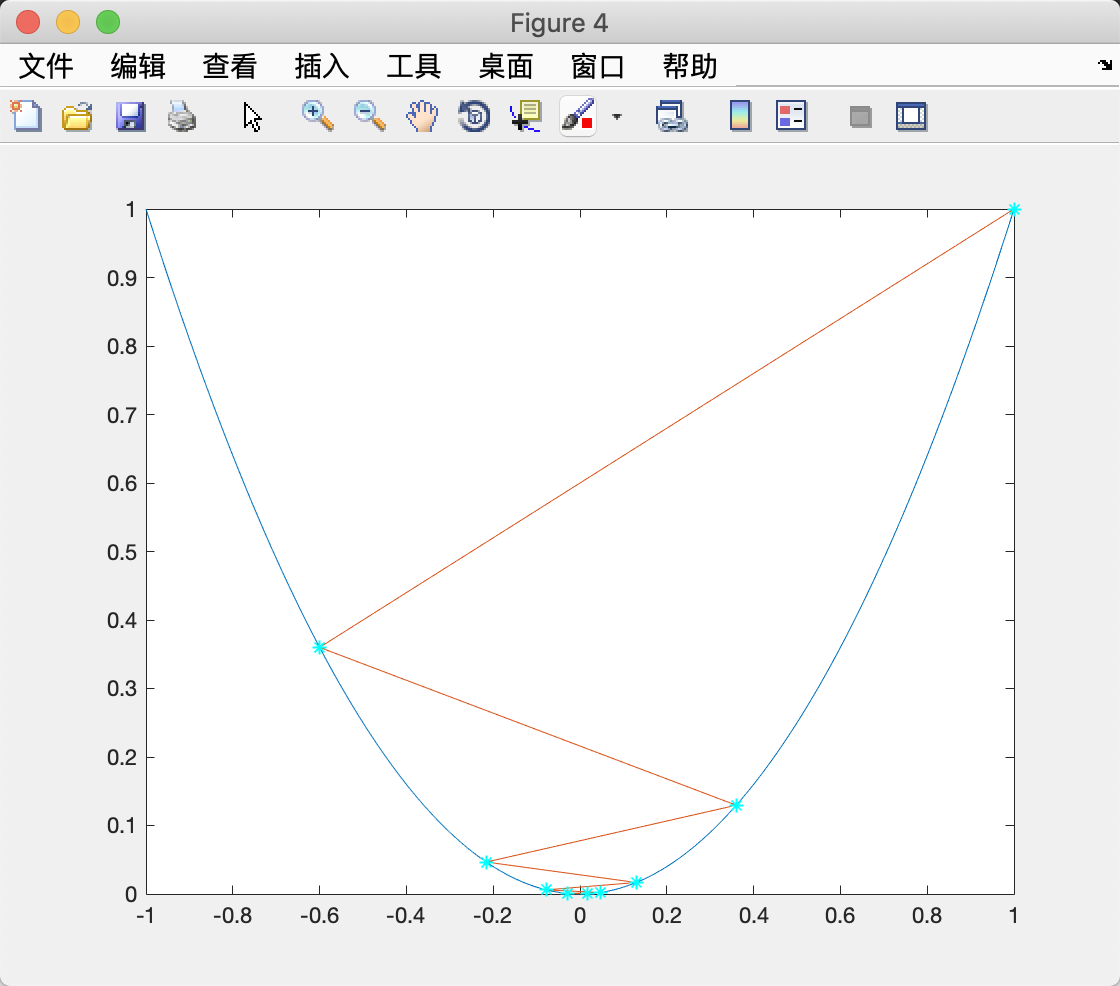
左图和右图分别为 $\alpha =0.3$ 和 $\alpha=0.7$ 时的效果。梯度下降法是一阶方法，其收敛速度通常不如二阶方法，如牛顿法。

牛顿法

所有二阶方法都源自二阶泰勒展开：
$f(\bm x + \delta\bm x) \approx f(\bm x)+\bm g^\top\delta\bm x+\dfrac{1}{2}\delta\bm x^\top\bm H\delta\bm x$
其中 $\bm g = \frac{df}{d\bm x}(\bm x)$ ， $\bm H = \frac{df^2}{d\bm x^2}(\bm x)$

最低0.47元/天解锁文章