机器学习/深度学习中的常用损失函数公式、原理与代码实践（持续更新ing...）

诸神缄默不语

已于 2024-02-19 19:13:56 修改

阅读量1.5k

点赞数 2

分类专栏：人工智能学习笔记文章标签：深度学习 python 损失函数交叉熵

于 2022-06-12 13:28:43 首次发布

本文链接：https://blog.csdn.net/PolarisRisingWar/article/details/125244389

版权

人工智能学习笔记专栏收录该内容

268 篇文章

订阅专栏

诸神缄默不语-个人CSDN博文目录

本文的结构是首先介绍一些常见的损失函数，然后介绍一些个性化的损失函数实例。

文章目录

1. 分类 - 交叉熵
2. 分类 - hinge loss
- 2.1 二分类
- 2.2 多分类
3. 分类 - 不平衡问题 - focal loss
3. 回归 - MSE
4. 对比学习/度量学习
5. 罚项
6. 魔改损失函数的示例
7. 代码撰写常见问题
8. 其他文中未提及的参考资料

1. 分类 - 交叉熵

讲解博文：

1.1 二分类 - BCELoss系

二分类可以使用BCELoss，比如链路预测任务预测某条边是否存在，或者多标签分类中将每个类作为一个二分类任务（但是一般来说这样效果会很差），就用BCELoss。
torch.nn.BCEWithLogitsLoss=sigmoid (torch.special.expit) +torch.nn.BCELoss
BCEWithLogitsLoss — PyTorch 1.12 documentation

直接使用torch.nn.BCEWithLogitsLoss在数学上更稳定。
torch.nn.BCEWithLogitsLoss(weight=None, size_average=None, reduce=None, reduction='mean', pos_weight=None)

单标签二分类（一般都是这样的）：

loss = nn.BCEWithLogitsLoss()
input = torch.randn(3, requires_grad=True)
target = torch.empty(3).random_(2)
output = loss(input, target)
output.backward()

BCELoss和sigmoid分开的写法：（这个标签和预测结果就是多标签二分类，只是展开了）

loss_func=nn.BCELoss()
logp=torch.special.expit(logits)
loss=loss_func(logp.view(-1),train_label.view(-1))

多标签二分类：

target = torch.ones([10, 64], dtype=torch.float32)  # 64 classes, batch size = 10
output = torch.full([10, 64], 1.5)  # A prediction (logit)
pos_weight = torch.ones([64])  # All weights are equal to 1
criterion = torch.nn.BCEWithLogitsLoss(pos_weight=pos_weight)
criterion(output, target)  # -log(sigmoid(1.5))

输出：tensor(0.2014)

其他相关参考资料：

1.2 多分类

CrossEntropyLoss

CrossEntropyLoss（等于softmax+NLLLoss）

CrossEntropyLoss的入参：

weight：权重（Tensor对象，且要么该对象和CrossEntropyLoss对象的Tensor对象入参在同样的设备上，要么将整个CrossEntropyLoss对象放到入参所在的设备上，否则会报错）
示例：weight=torch.from_numpy(np.array([0.1,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0])).float())，然后weight=weight.to(cuda_device)再criterion=nn.CrossEntropyLoss(weight=weight)，或者先criterion=nn.CrossEntropyLoss(weight=weight)再criterion.to(cuda_device)

代码用法：

torch.nn.CrossEntropyLoss()(标签,预测出的logits)

注意，这里的标签可以是每个样本对应的标签向量（值为1的标签是ground-truth），也可以是每个样本对应的标签索引（取值为0至(标签数-1)）

softmax + NLLLoss

有些情况下，在nn.Module的forward()中就已经对logits进行了归一化。在这种情况下就直接对输出用NLLLoss即可：

criterion=nn.NLLLoss()

loss=criterion(torch.log(logits + 1e-8),labels)

完整代码可参考：https://github.com/PolarisRisingWar/LJP_Collection/blob/master/models/MPBFN/train_and_test.py

1.3 sparse softmax

参考论文：

(2016) From Softmax to Sparsemax: A Sparse Model of Attention and Multi-Label Classification
(2019 ACL) Sparse Sequence-to-Sequence Models
1. 论文笔记：稀疏序列到序列模型 - 知乎

通用参考资料：

苏神版：
总之大致来说就是仅用概率最高的k个类别的概率来通过softmax和交叉熵

2. 分类 - hinge loss

2.1 二分类

真实标签 $t = \pm 1$ ，分类器预测得分 $y$ ，损失函数： $l(y)=\max(0,1-t\cdot y)$ （1是margin）

hinge loss图像（图中蓝色线），以 $t y$ 为横轴， $l$ 为纵轴：
在这里插入图片描述
（图中绿色线是zero-one loss）

hinge loss要求 $t y \geq 1$ ，就是要求分类正确的节点离分类界线尽量远。也就是模型需要将节点正确划分到超过阈值的程度。

在SVM中使用。

参考资料：

Hinge loss - Wikiwand：这篇写得有问题
怎么样理解SVM中的hinge-loss？ - 知乎：这里面的回答太进阶了，没看懂。

2.2 多分类

在这里插入图片描述
（图源：Hinge loss - Wikipedia，所谓 $w x$ 就是指分类器的预测得分）

3. 分类 - 不平衡问题 - focal loss

原论文：Focal Loss for Dense Object Detection

找了个解释的博文，但是没看懂：Focal loss论文详解 - 知乎

3. 回归 - MSE

https://pytorch.org/docs/stable/generated/torch.nn.MSELoss.html

import torch
import torch.nn as nn

loss = nn.MSELoss()
input = torch.randn(3, 5, requires_grad=True)
target = torch.randn(3, 5)
output = loss(input, target)
output.backward()

关于用MSE还是RMSE进行梯度下降，可以参考这个帖子：Why do we use RMSE instead of MSE? - PyTorch Forums 也没有给出具体的回答，回复者只说他个人倾向于用MSE，具体的解释我没有看懂

4. 对比学习/度量学习

4.1 triplet (ranking) loss

这是给出一个三元组，原样本-相似样本-不相似样本，然后用损失函数诱使相似样本对靠近，不相似样本对离远：
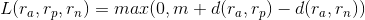
在这里插入图片描述

另一种写法（应该是等价的吧）就写成这样：

FaceNet: A Unified Embedding for Face Recognition and Clustering：
在这里插入图片描述

4.2 pairwise ranking loss

给出一对样本，将正样本对（相似样本）之间的距离拉小，负样本对之间的距离拉大。

在这里插入图片描述
（m是margin）

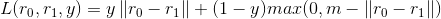
在这里插入图片描述
（y是样本对的正负性标签）

当样本对是正例时，其样本对的距离越大则L值越大；当是负例时则反之，但距离越大越好，但若超过一定阈值m，则该样本对对模型带来的影响就微乎其微，因此直接设置为零。

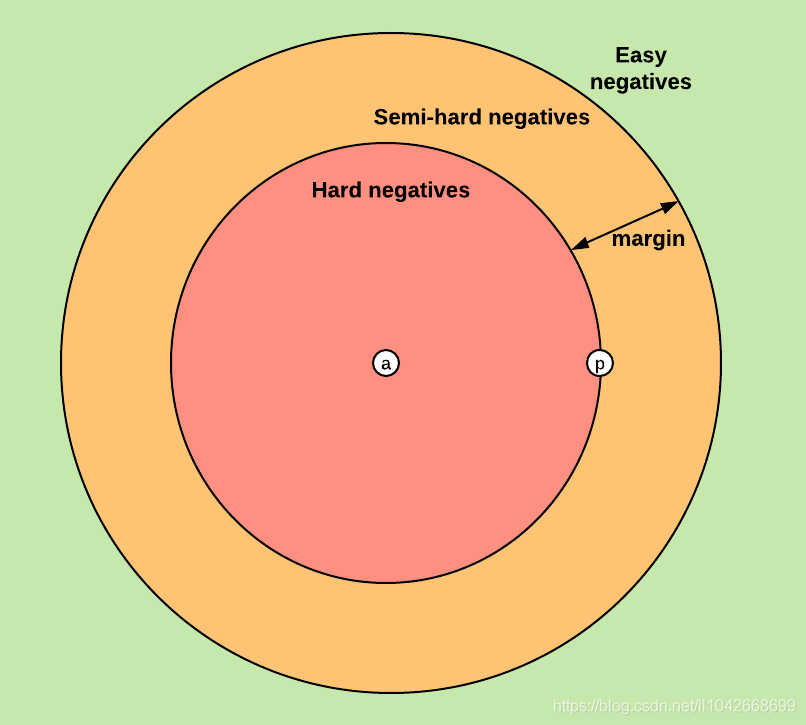
在这里插入图片描述
n(negative)样本可以分布在图中的任意区域，与a(anchor样本)的距离代表二者的相似度,距离越远相似度越小，模型的目标就是让正样例样本对p-a之间的距离变小，负样例样本对n-1的距离变大。

4.3 InfoNCE loss

希望从一个正样本对和n-1个负样本对中间使得正样本对之间的embedding距离拉得更近

5. 罚项

参考资料：

这篇看了一遍，没太学好：Intuitions on L1 and L2 Regularisation | by Raimi Karim | Towards Data Science
ML 入门：归一化、标准化和正则化 - 知乎：这篇写得挺清晰的，我主要简单看了一下LP范数/正则项的部分

6. 魔改损失函数的示例

多任务：一般来说就是直接加起来
1. 我之前写过：用huggingface.transformers在文本分类任务（单任务和多任务场景下）上微调预训练模型
2. SPACES模型，示例损失函数部分TensorFlow1+Keras代码：SPACES/seq2seq_model.py at main · bojone/SPACES
自定义：图神经网络节点表征模型PTA，PyTorch代码，我参考原始项目复现出来的。损失函数分成2部分，一部分在模型中直接定义随epoch变化的损失函数：rgb-experiment/pta.py at master · PolarisRisingWar/rgb-experiment，一部分在训练和测试的时候额外增加设定的超参：rgb-experiment/itexperiments.py at master · PolarisRisingWar/rgb-experiment
多任务+自定义：legal judgment prediction模型EPM：在train()函数中，又是多任务，又加了mask（在原论文中定义为“constraint”）：EPM/model.py at main · WAPAY/EPM