JPS寻路算法的学习笔记

Zephyr_MrR

已于 2024-09-26 15:51:00 修改

阅读量1.5k

点赞数 23

分类专栏：寻路文章标签：算法

于 2024-09-24 21:18:07 首次发布

本文链接：https://blog.csdn.net/Suphyr/article/details/142498123

版权

寻路专栏收录该内容

1 篇文章

订阅专栏

JPS（Jump Point Search）寻路算法的学习笔记

A*算法
JPS算法
JPS代码（MATLAB）

JPS寻路算法是用于加速A* 路径搜索的优化算法，在了解其之前应当先了解A* 算法的本质。

A*算法

A*（A-Star)算法是一种静态网络中求解最短路径的常用方法之一，基于深度优先算法(Depth First Search, DFS)和广度优先算法(Breadth First Search, BFS)，按照一定原则不断地由起点向终点拓展路径。

A* 算法是一种启发式搜索算法，结合了最佳优先搜索和Dijkstra算法的优点。它通过评估路径的成本（G）和启发式估计（H）来找到最优路径。其主要思想是：

节点评估

$F = G + H$

F：从起点到终点的总估计成本
G：从起点到当前节点的实际成本。
H：从当前节点到终点的估计成本。

一般的启发式函数包括：

曼哈顿距离（适用于只能在网格中水平或垂直移动的情况）： $H = |x_1 - x_2| + |y_1 - y_2|$
欧几里得距离（适用于可以在任意方向移动的情况）： $\sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2}$
切比雪夫距离（适用于可以在对角线移动的情况）： $H = max(|x_1 - x_2| , |y_1 - y_2|)$

优先级队列

A* 算法维护一个优先级队列（一般称为openList表），记录待考察的节点，根据其来选择评估值(F值)最低的节点进行扩展，已经考察过的节点从openList表中删除，加入closeList表。

路径寻找

不断扩展节点，直到找到目标节点或者不再有新的可扩展节点（即没有找到通往终点的路径）。

小结

A*算法的优点在于它能高效地找到起点到终点之间的最短路径，且由于使用了启发式信息，通常比Dijkstra算法快。

JPS算法

JPS算法是对A* 算法的一种优化。A*算法在扩展节点时会把所有相邻的节点考虑进去，当地图比较大时，openList 中的节点数量会很多，搜索效率较低，当两点之间没有障碍物时，中间的节点是不希望添加到 openList中的，而只有跳跃性的或者说需要转弯的节点才会被考虑，即跳点（Jump Point）。

JPS的主要思想就是通过跳跃来减少需要检查的节点数，从而提高效率。

然而本人在学习过程中，对于网上现存的很多资料感到困惑，尤其是其对于跳点、强迫邻居的解释。在此笔者根据自己的理解对其判断进行了简化，希望能够帮助更多人简单理解本算法的细节。

跳点

通俗来讲就是在路径上能通过改变移动方向绕过障碍物的点就是跳点，如图中的X节点：

在这里插入图片描述

判断一个节点是不是跳点，遵循以下原则：

(1)节点是起点、终点。

(2)节点至少有一个强迫邻居（Foced Neighbor）。

(3)父节点沿对角线到达该节点，该节点的水平或者垂直方向上有满足 (1)、(2) 的节点（如图中的A节点）。

在这里插入图片描述

强迫邻居

其严格的数学定义是：节点X的邻居节点有障碍物，且X的父节点P经过X到达N的距离代价，比不经过X到大N的任一路径的距离代价都小，则称N是X的强迫邻居。

这句话很绕，但可以通过如下几幅图来进行说明：
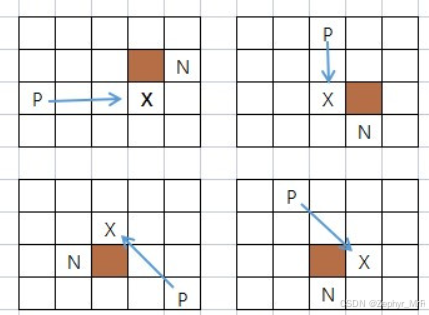
在这里插入图片描述

跳点的简单判定

根据跳点的判断原则（3），当父节点对角线跳跃（dx!=0，dy!=0）时，需要递归检查直线方向，若存在跳点，该节点即为跳点。因此我们可以仅讨论直线跳跃与对角线跳跃时自身有无强迫邻居的情况。

此种情况下，其实可以直接将其定义转化为：

父节点水平方向跳跃（dx!=0，dy=0）：节点X的上下节点之一有障碍物，且障碍物的dx方向没有。

在这里插入图片描述

父节点垂直方向跳跃（dx=0，dy!=0）：节点X的左右节点之一有障碍物，且障碍物的dy方向没有。

在这里插入图片描述

父节点对角线方向跳跃（dx!=0，dy!=0）：节点X的-dx方向节点有障碍物，且障碍物的dy方向节点没有或者 X的-dy方向节点有障碍物，且障碍物的dx方向节点没有（可自行画图对每一种情况进行验证）。

在这里插入图片描述

当满足以上条件时，则可以判定该节点为跳点。

两种算法的对比展示

在这里插入图片描述

图中白色部分代表可行点，黑色部分代表障碍物，黄色部分代表加入过openlist的点，红圈代表起点，绿圈代表终点，绿线代表最短路径

小结

通过对A*算法中的openList进行精简，可以提高搜索的效率，但一定情况下由于对跳点的搜索占用了大量的计算资源，二者的计算时间差异并不显著甚至JPS算法会更慢，若能提前对静态地图进行预处理，则可进一步提升搜索效率（JPS+算法）。

JPS代码（MATLAB）

clc;clear;
% 设置栅格地图的大小 (10x10)
mapSizeX = 20;
mapSizeY = 20;

% 创建一个栅格地图，初始为可行区域，0代表可行区域
map = zeros(mapSizeX, mapSizeY);


% 创建随机障碍物，确保留出一条路径(map(i, j) = 1表示有障碍物，map(i, j) = 0表示可通行)
for i = 1:20
    for j = 1:20
        if rand < 0.3 % 30% 的概率设置为障碍物
            map(i, j) = 1; % 障碍物
        else
            map(i, j) = 0; % 可通行区域
        end
        % 确保保持从 (1, 1) 到 (20, 20) 的通道
        if i == 20
            map(i, j) = 0; % 最后一行通道
        end
        if j == 20
            map(i, j) = 0; % 最后一列通道
        end
    end
end
map(1,1)=0;
map(20,20)=0;

% 定义起点和终点
start = [1, 1];
goal = [20, 20];

% 开始计时
tic;
% A*路径规划
[pathAStar, searchedPointsAStar,totalCostAStar, fScoreAStar] = AStar(map, start, goal);
% 结束计时并显示运行时间
elapsedTime = toc;
fprintf('AStar 算法运行时间为: %.4f 秒\n', elapsedTime);
% 输出路径的总代价
fprintf('AStar 算法路径的总代价为: %.2f\n', totalCostAStar);

% 开始计时
tic;
% JPS路径规划
[pathJPS, searchedPointsJPS, totalCostJPS, fScoreJPS] = JPS(map, start, goal);
% 结束计时并显示运行时间
elapsedTime = toc;
fprintf('JPS 算法运行时间为: %.4f 秒\n', elapsedTime);
% 输出路径的总代价
fprintf('JPS 算法路径的总代价为: %.2f\n', totalCostJPS);

% 创建固定大小的figure窗口
fig = figure('Position', [100, 100, 1000, 600]); % [left, bottom, width, height]

% 可视化二者的搜索结果
fprintf('图中白色部分代表可行点，黑色部分代表障碍物，黄色部分代表加入过openlist的点，红圈代表起点，绿圈代表终点，绿线代表最短路径\n');

% 绘制第一个算法的地图和路径
plotGridMap(map, fScoreAStar, searchedPointsAStar, pathAStar, start, goal, 1, 'Algorithm AStar Visualization');

% 绘制第二个算法的地图和路径
plotGridMap(map, fScoreJPS, searchedPointsJPS, pathJPS, start, goal, 2, 'Algorithm JPS Visualization');


function plotGridMap(map, fScore, searchedPoints, path, start, goal, subplotIndex, titleText)
    % 绘制栅格地图、搜索过的点和最终路径
    mapSizeX = size(map, 1);
    mapSizeY = size(map, 2);
    
    % 创建一个subplot
    subplot(1, 2, subplotIndex);
    hold on;
    
    % 绘制栅格地图
    for x = 1:mapSizeX
        for y = 1:mapSizeY
            if map(x, y) == 1
                % 绘制障碍物 (用黑色方块表示)
                fill([x-1, x, x, x-1], [y-1, y-1, y, y], 'k');
            else
                % 绘制可行区域 (用白色方块表示)
                fill([x-1, x, x, x-1], [y-1, y-1, y, y], 'w');
            end
        end
    end

    % 绘制搜索过的点
    for i = 1:size(searchedPoints, 1)
        x = searchedPoints(i, 1);
        y = searchedPoints(i, 2);
        % 用黄色方块表示搜索过的点
        fill([x-1, x, x, x-1], [y-1, y-1, y, y], 'y');
%         % 在格子中央显示 gScore 的值
%         text(x-0.5, y-0.5, sprintf('%.2f', fScore(x, y)), ...
%              'HorizontalAlignment', 'center', 'FontSize', 5, 'Color', 'r');
    end

    % 绘制最终路径（穿越格子中心的直线）
    for i = 1:size(path, 1)-1
        x1 = path(i, 1) - 0.5;  % 格子中心的 X 坐标
        y1 = path(i, 2) - 0.5;  % 格子中心的 Y 坐标
        x2 = path(i+1, 1) - 0.5; % 下一个格子中心的 X 坐标
        y2 = path(i+1, 2) - 0.5; % 下一个格子中心的 Y 坐标
        plot([x1, x2], [y1, y2], 'g-', 'LineWidth', 1); % 绘制直线，绿色，线宽为2
    end

    % 标记起点和终点
    plot(start(1)-0.5, start(2)-0.5, 'ro', 'MarkerSize', 10, 'LineWidth', 2); % 起点用红色圆圈表示
    plot(goal(1)-0.5, goal(2)-0.5, 'go', 'MarkerSize', 10, 'LineWidth', 2); % 终点用绿色圆圈表示

    % 设置坐标轴样式
    axis equal;
    axis([0 mapSizeX 0 mapSizeY]);

    % 设置坐标原点在左下角，x和y轴的标签
    set(gca, 'XTick', 0:mapSizeX, 'YTick', 0:mapSizeY);
    set(gca, 'XAxisLocation', 'bottom', 'YAxisLocation', 'left');
    xlabel('X');
    ylabel('Y');
    title(titleText);

    % 添加网格线
    grid on;
    set(gca, 'GridLineStyle', '-');
end

function [path, searchedPoints, totalCost, fScore] = AStar(map, start, goal)
    % 启发式函数为曼哈顿距离
    heuristic = @(a, b) sqrt((a(1)-b(1))^2+ (a(2)-b(2))^2);

    % 初始化
    openSet = start;
    cameFrom = zeros(size(map, 1), size(map, 2), 2); % 用来回溯路径
    gScore = inf(size(map));
    gScore(start(1), start(2)) = 0;
    fScore = inf(size(map));
    fScore(start(1), start(2)) = heuristic(start, goal);
    
    searchedPoints = [];
    
    while ~isempty(openSet)
        % 找到openSet中f值最小的节点
        current = openSet(1, :);
        for i = 2:size(openSet, 1)
            if fScore(openSet(i, 1), openSet(i, 2)) < fScore(current(1), current(2))
                current = openSet(i, :);
            end
        end
        
        % 到达终点
        if isequal(current, goal)
            path = reconstructPath(cameFrom, current);
            totalCost = gScore(goal(1), goal(2)); % 返回终点的gScore作为总代价
            return;
        end
        
        % 从openSet中移除当前节点
        openSet(openSet(:, 1) == current(1) & openSet(:, 2) == current(2), :) = [];
        
        % 记录搜索过的点
        searchedPoints = [searchedPoints; current];
        
        % 邻居节点，包括对角线方向
        neighbors = [current(1)-1, current(2);    % 上
                     current(1)+1, current(2);    % 下
                     current(1), current(2)-1;    % 左
                     current(1), current(2)+1;    % 右
                     current(1)-1, current(2)-1;  % 左上
                     current(1)-1, current(2)+1;  % 右上
                     current(1)+1, current(2)-1;  % 左下
                     current(1)+1, current(2)+1]; % 右下
        
        for i = 1:8
            neighbor = neighbors(i, :);
            if neighbor(1) < 1 || neighbor(2) < 1 || neighbor(1) > size(map, 1) || neighbor(2) > size(map, 2)
                continue; % 超出边界
            end
            if map(neighbor(1), neighbor(2)) == 1
                continue; % 遇到障碍物
            end
            
            % 根据移动方向判断移动代价
            if i <= 4
                % 水平或垂直移动的代价为 1
                moveCost = 1;
            else
                % 对角线移动的代价为 sqrt(2)
                moveCost = sqrt(2);
            end
            
            tentative_gScore = gScore(current(1), current(2)) + moveCost;
            if tentative_gScore < gScore(neighbor(1), neighbor(2))
                % 更新路径
                cameFrom(neighbor(1), neighbor(2), :) = current;
                gScore(neighbor(1), neighbor(2)) = tentative_gScore;
                fScore(neighbor(1), neighbor(2)) = gScore(neighbor(1), neighbor(2)) + heuristic(neighbor, goal);
                if isempty(find(openSet(:, 1) == neighbor(1) & openSet(:, 2) == neighbor(2), 1))
                    openSet = [openSet; neighbor]; % 添加到openSet
                end
            end
        end
    end
    
    error('未找到路径');
end

% 回溯路径
function path = reconstructPath(cameFrom, current)
    path = current;
    while all(cameFrom(current(1), current(2), :))
        current = squeeze(cameFrom(current(1), current(2), :))';
        path = [current; path];
    end
end

function [path, searchedPoints, totalCost, fScore] = JPS(map, start, goal)
    % 启发式函数为曼哈顿距离
    heuristic = @(a, b) sqrt((a(1)-b(1))^2+ (a(2)-b(2))^2);

    % 初始化
    openSet = start;
    cameFrom = zeros(size(map, 1), size(map, 2), 2); % 用来回溯路径
    gScore = inf(size(map));
    gScore(start(1), start(2)) = 0;
    fScore = inf(size(map));
    fScore(start(1), start(2)) = heuristic(start, goal);
    
    searchedPoints = [];
    
    while ~isempty(openSet)
        % 找到openSet中f值最小的节点
        current = openSet(1, :);
        for i = 2:size(openSet, 1)
            if fScore(openSet(i, 1), openSet(i, 2)) < fScore(current(1), current(2))
                current = openSet(i, :);
            end
        end
        
        % 到达终点
        if isequal(current, goal)
            path = reconstructPath(cameFrom, current);
            totalCost = gScore(goal(1), goal(2));  % 返回路径总代价
            return;
        end
        
        % 从openSet中移除当前节点
        openSet(openSet(:, 1) == current(1) & openSet(:, 2) == current(2), :) = [];
        
        % 记录搜索过的点
        searchedPoints = [searchedPoints; current];
        
        % 获取跳点邻居节点
        neighbors = getJumpPoints(map, current, start, goal, gScore, heuristic);
        
        for i = 1:size(neighbors, 1)
            neighbor = neighbors(i, :);
            tentative_gScore = gScore(current(1), current(2)) + distance(current, neighbor);
            if tentative_gScore < gScore(neighbor(1), neighbor(2))
                % 更新路径
                cameFrom(neighbor(1), neighbor(2), :) = current;
                gScore(neighbor(1), neighbor(2)) = tentative_gScore;
                fScore(neighbor(1), neighbor(2)) = gScore(neighbor(1), neighbor(2)) + heuristic(neighbor, goal);
                if isempty(find(openSet(:, 1) == neighbor(1) & openSet(:, 2) == neighbor(2), 1))
                    openSet = [openSet; neighbor]; % 添加到openSet
                end
            end
        end
    end
    
    error('未找到路径');
end

% 获取跳点邻居
function neighbors = getJumpPoints(map, current, start, goal, gScore, heuristic)
    directions = [0, 1;    % 上
                  0, -1;   % 下
                  1, 0;    % 右
                 -1, 0;    % 左
                  1, 1;    % 右上
                 -1, 1;    % 左上
                  1, -1;   % 右下
                 -1, -1];  % 左下
    neighbors = [];
%     fprintf('跳点（%d,%d）的邻居是：\n', current);
    for i = 1:size(directions, 1)
        dir = directions(i, :);
        jumpPoint = jump(map, current, goal, dir, gScore);
        if ~isempty(jumpPoint)
%             fprintf('跳点（%d,%d）\n', jumpPoint);
            neighbors = [neighbors; jumpPoint];
        end
    end
end

% 跳点搜索逻辑
% 通俗一点的讲就是在路径上改变移动方向的点就是跳跃点
function jumpPoint = jump(map, node, goal, direction, gScore)
    x = node(1);
    y = node(2);
    dx = direction(1);
    dy = direction(2);
    
    % 跳跃过程中不断前进
    while true
        x = x + dx;
        y = y + dy;
        
        % 边界检查
        if x < 1 || x > size(map, 1) || y < 1 || y > size(map, 2) || map(x, y) == 1
            jumpPoint = [];
            return;
        end
        
        % 如果到达终点
        if isequal([x, y], goal)
            jumpPoint = [x, y];
            return;
        end

        % 如果是对角线跳跃，递归检查直线方向（若存在跳点，则为跳点）
        if dx ~= 0 && dy ~= 0
            if ~isempty(jump(map, [x, y], goal, [dx, 0], gScore)) || ...
               ~isempty(jump(map, [x, y], goal, [0, dy], gScore))
                jumpPoint = [x, y];
                return;
            end
        end

        % 如果是直线跳跃（dx、dy有一方为0），检查强制邻居（有即为跳点）
        if hasForcedNeighbor(map, [x, y], direction)
            jumpPoint = [x, y];
            return ;
        end
        

    end
end

% 检查强制邻居
function forced = hasForcedNeighbor(map, node, direction)
% 强制邻居： 节点X的邻居节点有障碍物，且X的父节点P经过X到达N的距离代价，比不经过X到大N的任一路径的距离代价都小，则称N是X的强迫邻居。
    x = node(1);
    y = node(2);
    dx = direction(1);
    dy = direction(2);
    
    forced = false;

    % 对角方向检测：满足下列两个条件之一
    if (dx ~= 0 && dy ~= 0)
        % X的-dx方向节点有障碍物，且障碍物的dy方向节点没有 或者 X的-dy方向节点有障碍物，且障碍物的dx方向节点没有
        if (x - dx >= 1 && x - dx <= size(map, 1) && y + dy >= 1 && y + dy <= size(map, 2) && map(x-dx, y) == 1 && map(x-dx, y+dy) == 0) || ...
           (y - dy >= 1 && y - dy <= size(map, 2) && x + dx >= 1 && x + dx <= size(map, 1) && map(x, y-dy) == 1 && map(x+dx, y-dy) == 0)
            forced = true;
            return ;
        end
        return ;
    end

    % 水平方向检测：X的上下节点有障碍物，且障碍物的dx方向节点没有
    if dx ~= 0
        if (y > 1 && x + dx >= 1 && x + dx <= size(map, 1) && map(x, y-1) == 1 && map(x+dx, y-1) == 0) || ...
           (y < size(map, 2) && x + dx >= 1 && x + dx <= size(map, 1) && map(x, y+1) == 1 && map(x+dx, y+1) == 0)
            forced = true;
            return ;
        end
        return ;
    end

    % 垂直方向检测：X的左右节点有障碍物，且障碍物的dy方向节点没有
    if dy ~= 0
        if (x > 1 && y + dy >= 1 && y + dy <= size(map, 2) && map(x-1, y) == 1 && map(x-1, y+dy) == 0) || ...
           (x < size(map, 1) && y + dy >= 1 && y + dy <= size(map, 2) && map(x+1, y) == 1 && map(x+1, y+dy) == 0)
            forced = true;
            return ;
        end
        return ;
    end

end

% 计算当前节点到目标节点的曼哈顿距离
function d = distance(a, b)
    d = sqrt((a(1) - b(1))^2 + (a(2) - b(2))^2);
end

% 回溯路径
function path = reconstructPath(cameFrom, current)
    path = current;
    while all(cameFrom(current(1), current(2), :))
        current = squeeze(cameFrom(current(1), current(2), :))';
        path = [current; path];
    end
end