一、在MATLAB命令中输入help zpk()会出现这样解释:
zpk - Create zero-pole-gain model; convert to zero-pole-gain model
This MATLAB function creates a continuous-time zero-pole-gain model with zeros
Z, poles P, and gain(s) K.
意思是该函数可以创建连续时间零极点模型,具体用法如下:
例如你要建立开环零极点形式的传递函数:100*(s+5)/[(s-2)*(s+8)*(s+20)],并作出Nyquist曲线并判断稳定性?
Matlab编程如下:
k=100;
z=-5;
p=[2,-8,-20];
G=zpk(z,p,k)
nyquist(G);grid
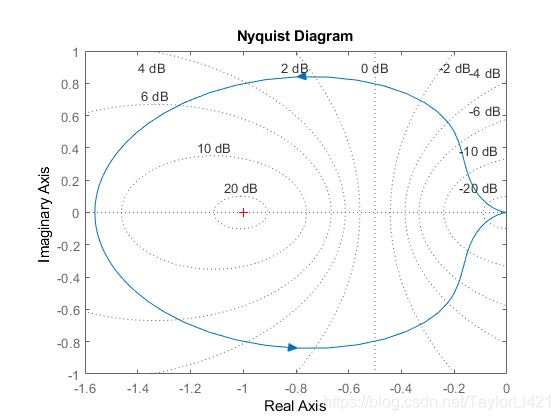










 本文介绍了如何使用MATLAB的zpk函数创建连续时间零极点增益模型,并通过Nyquist图判断系统稳定性。通过实例演示了创建开环传递函数及稳定性分析的过程。
本文介绍了如何使用MATLAB的zpk函数创建连续时间零极点增益模型,并通过Nyquist图判断系统稳定性。通过实例演示了创建开环传递函数及稳定性分析的过程。
















 4026
4026

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








