【Koopman 算子】深度学习用于非线性动力学的通用线性嵌入研究（Python、Matlab代码实现）

长安程序猿

于 2025-03-03 09:03:00 发布

阅读量1.4k

点赞数 24

文章标签：深度学习 python matlab

本文链接：https://blog.csdn.net/Yan_she_He/article/details/145975468

版权

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

⛳️赠与读者

💥1 概述

深度学习与Koopman算子结合的非线性动力学通用线性嵌入研究综述

一、Koopman算子的理论基础与非线性系统线性化

二、深度学习在Koopman算子近似中的角色

三、通用线性嵌入（Generalized Linear Embedding）的实现方式

四、最新研究进展与挑战

五、应用案例

六、未来方向

总结

📚2 运行结果

🎉3 参考文献

🌈4 Python、Matlab代码、文章下载

⛳️赠与读者

👨‍💻做科研，涉及到一个深在的思想系统，需要科研者逻辑缜密，踏实认真，但是不能只是努力，很多时候借力比努力更重要，然后还要有仰望星空的创新点和启发点。建议读者按目录次序逐一浏览，免得骤然跌入幽暗的迷宫找不到来时的路，它不足为你揭示全部问题的答案，但若能解答你胸中升起的一朵朵疑云，也未尝不会酿成晚霞斑斓的别一番景致，万一它给你带来了一场精神世界的苦雨，那就借机洗刷一下原来存放在那儿的“躺平”上的尘埃吧。

或许，雨过云收，神驰的天地更清朗.......🔎🔎🔎

💥1 概述

发现能够使强非线性动力学近似线性化的坐标变换，有望借助线性理论实现非线性的预测、估计和控制。Koopman 算子是一种领先的数据驱动嵌入方法，其特征函数提供了能够全局线性化动力学的内在坐标。然而，识别和表示这些特征函数一直是一个挑战。本研究利用深度学习从数据中发现 Koopman 特征函数的表示。我们的网络在构建时就是简洁且可解释的，将动力学嵌入到低维流形上。我们通过改进的自编码器识别出动力学在全球范围内线性化的非线性坐标。我们还将 Koopman 表示推广到包括具有连续谱的普遍系统类别。我们的框架使用辅助网络对连续频率进行参数化，从而实现紧凑且高效的嵌入，同时将我们的模型与数十年的渐近分析相联系。因此，我们既利用了深度学习的强大能力，又保留了 Koopman 嵌入的物理可解释性。

非线性是复杂系统的标志性特征，它在物理、生物和工程科学中引发了丰富多样的动态行为。尽管从计算角度来看是可行的，但目前并不存在用于求解非线性动态系统的通用数学框架。因此，将非线性动态表示在线性框架中特别具有吸引力，因为线性系统具有强大且全面的分析和控制技术，而这些技术并不容易推广到非线性系统。Koopman 算子理论于 1931 年发展起来，近年来已成为系统地线性表示非线性系统的领先候选方法。这种对 Koopman 分析的重新关注是由理论进展、改进的数值方法（如动态模态分解，DMD）以及数据的日益丰富共同推动的。Koopman 算子的特征函数现在被广泛寻求，因为它们提供了能够全局线性化非线性动态的内在坐标。尽管 Koopman 嵌入具有巨大的潜力，但在最简单的系统之外，获取其表示已被证明是困难的，而且这些表示通常复杂得难以处理，或者是不可解释的黑箱优化的输出。在本工作中，我们利用深度学习的强大能力来灵活且一般地表示 Koopman 算子，同时强制执行一种促进结果模型简洁性和可解释性的网络结构。

神经网络（NN），作为深度学习的理论架构，最初是受到猫的初级视觉皮层的启发，那里的神经元以分层的细胞结构组织起来以处理视觉刺激。第一个数学模型是新认知机，它具有现代深度神经网络（DNN）的许多特征，包括多层结构、卷积、最大池化和非线性动态节点。重要的是，通用近似定理保证了一个具有足够多隐藏单元和线性输出层的神经网络能够表示任意函数，包括我们期望的 Koopman 特征函数。尽管神经网络已有四十年的历史，但对包含超过 1500 万张标记图像的 ImageNet 数据集的分析是一个分水岭时刻。事实上，在大数据的兴起和计算能力增强的推动下，深度学习正在许多数据驱动的分类和识别任务中取得变革性进展。深度学习的一个优势是数据特征是分层构建的，这使得复杂函数的表示成为可能。因此，深度学习可以在没有手工设计特征或用户选择合适基函数的情况下准确拟合函数。然而，当前深度学习研究的一个挑战是识别简洁、可解释且可转移的模型。

深度学习有潜力实现一种可扩展且数据驱动的架构，用于发现和表示 Koopman 特征函数，从而为强非线性系统提供内在的线性表示。这种方法缓解了现代动态系统中的两个关键挑战：（1）对于气候、神经科学、流行病学和金融等领域的系统，其方程通常是未知的；（2）低维动态通常嵌入在高维状态空间中，需要能够发现潜在变量动态的可扩展架构。尽管几十年来神经网络也已被用于建模动态系统和其他物理过程，但近年来在使用 DNN 学习 Koopman 嵌入方面取得了巨大进展，并产生了许多优秀的论文。例如，VAMPnet 架构使用时间延迟自编码器和自定义变分评分，在令人印象深刻的蛋白质折叠示例中识别 Koopman 坐标。在所有这些最近的研究中，DNN 表示已被证明比其他领先方法更灵活，并且在具有挑战性的问题上具有更高的准确性。

本研究的重点是开发 DNN 表示的 Koopman 特征函数，即使对于高维和强非线性系统，这些表示也保持可解释性和简洁性。我们的方法（见图 1）与以往研究不同，因为我们专注于获得简洁的模型，这些模型与内在低秩动态相匹配，同时避免过拟合并保持可解释性，从而融合了 DNN 架构和 Koopman 理论的最佳特性。特别是，许多动态系统具有连续的特征值谱，这使得使用现有的 DNN 或 Koopman 表示进行低维表示变得复杂。这项工作开发了一个通用框架，并强制执行新约束，专门设计用于以可解释的方式提取最少的有意义的特征函数。对于具有连续谱的系统，我们使用增强型网络对内在坐标上的线性动态进行参数化，避免了在谐波特征函数中的无限渐近展开。因此，得到的网络保持简洁，关键的特征函数是可解释的。我们在几个例子上展示了 Koopman 的深度学习方法，这些例子旨在说明该方法的优势，同时在经典动态系统方面保持直观。

深度学习与Koopman算子结合的非线性动力学通用线性嵌入研究综述

一、Koopman算子的理论基础与非线性系统线性化

Koopman算子是由Bernard O. Koopman于1931年提出的无限维线性算子，其核心思想是将非线性动力系统的演化映射到函数空间（Hilbert空间）中，通过观测函数的线性演化描述系统行为。具体来说，对于非线性系统 xk+1=F(xk)+1=F(xk)，Koopman算子 KK 作用于观测函数 ψ(x)，满足 Kψ(xk)=ψ(F(xk))=ψ(F(xk))，从而在函数空间中实现线性化。

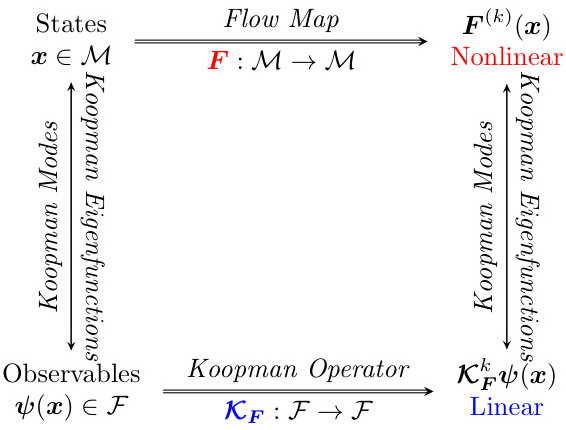
关键特性：

线性性：尽管原系统非线性，Koopman算子是严格线性的，允许使用线性代数工具分析系统。
谱分解：通过特征函数 ϕ(x)ϕ(x) 和特征值 λλ，可分解动力学为 Kϕ=λϕKϕ=λϕ，揭示系统的模态结构与长期行为。
不变子空间：若存在有限维不变子空间，则可通过有限维矩阵近似Koopman算子，实现降维建模。

二、深度学习在Koopman算子近似中的角色

传统方法（如动态模式分解DMD、扩展DMD）依赖人工选择基函数，难以处理复杂非线性系统。深度学习的引入解决了以下问题：

自动特征提取：神经网络（如自编码器）可自动学习非线性观测函数 ψ(x)ψ(x)，构建高维嵌入空间，使系统在该空间中线性演化。
端到端建模：通过编码器-解码器架构，编码器 ψ(x)ψ(x) 将状态映射到线性空间，解码器 ψ−1ψ−1 恢复原状态，结合线性动力学层（Koopman矩阵 KK）实现端到端训练。
处理高维数据：卷积神经网络（CNN）和时间序列网络（如LSTM）可处理流场、图像等复杂数据，扩展了Koopman理论的应用范围。

典型架构：

深度动态模式分解（DeepDMD） ：结合EDMD与神经网络，通过梯度下降优化字典函数，提升非线性表达能力。
Koopman神经算子（KNO） ：融合傅里叶变换与线性算子，在频域分离高频/低频模态，增强对偏微分方程的建模能力。
可解释网络（如EQL） ：生成显式数学方程而非黑箱模型，提升模型透明性。

三、通用线性嵌入（Generalized Linear Embedding）的实现方式

通用线性嵌入的目标是通过非线性映射将原系统状态提升至线性空间，其实现方式包括：

观测函数设计：
- 传统方法：多项式、径向基函数等，适用于简单系统。
- 深度学习方法：通过神经网络自动学习最优嵌入，例如：

变分自编码器（VAE） ：学习低维潜空间并强制线性动力学。
时间滞后自编码器：利用时间序列相关性构建Koopman不变子空间。

动力学线性化：

案例：

电力系统电压控制：通过Koopman嵌入将非线性电网模型转换为高维线性空间，结合模型预测控制（MPC）实现快速响应。
机器人姿态控制：使用深度Koopman模型预测非线性动力学，设计线性二次调节器（LQR）优化控制律。

四、最新研究进展与挑战

研究前沿：
- 可解释性提升：结合符号回归与神经网络，生成显式动力学方程（如EQL网络），平衡表达能力与可解释性。
- 多尺度建模：通过混合异质字典函数（如多项式、三角函数、神经网络），降低模型参数量的同时保持精度。
- 实时控制应用：端到端框架（如RLDK）消除解码器需求，提升计算效率，适用于自动驾驶和无人机。
关键挑战：
- 维度灾难：无限维Koopman算子的有限近似需权衡信息损失与计算复杂度。
- 非平稳系统：时变或混沌系统的Koopman谱结构复杂，难以保证线性嵌入的全局有效性。
- 数据依赖性：深度学习模型需大量高质量数据，而在实验科学中数据获取成本高。

五、应用案例

流体力学：通过Koopman模态分解湍流场，识别相干结构并预测能量传输。
生物分子动力学：VAMPnet架构分析蛋白质折叠路径，捕捉慢变自由度。
航天器控制：学习绳系卫星的Koopman模型，优化部署过程中的张力控制。

六、未来方向

物理引导学习：将已知守恒律（如哈密顿量）嵌入神经网络架构，提升泛化能力。
混合建模：结合稀疏识别（SINDy）与深度学习，从数据中同时发现方程结构与参数。
鲁棒性增强：开发对抗训练与不确定性量化方法，提升模型在噪声环境下的可靠性。

总结

Koopman算子与深度学习的结合为非线性动力学提供了“线性化-预测-控制”的全新范式。通过深度神经网络自动学习高维嵌入空间，不仅突破了传统线性方法的局限性，还在机器人、能源、生物等多个领域展现出广泛应用潜力。然而，如何在复杂系统中平衡模型表达能力、计算效率与可解释性，仍是未来研究的核心挑战。

📚2 运行结果

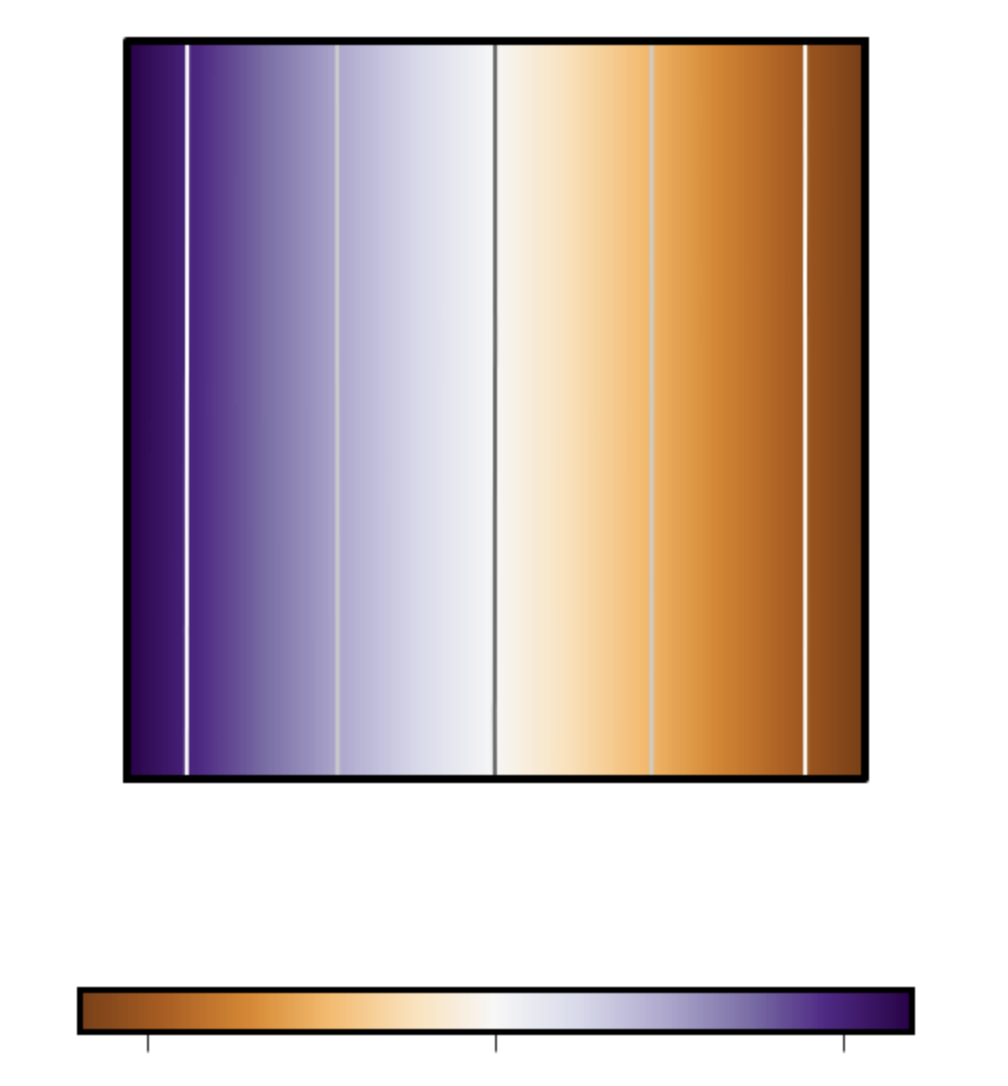
部分代码：

import copy

import training

params = {}

# settings related to dataset
params['data_name'] = 'FluidFlowOnAttractor'
params['data_train_len'] = 3
params['len_time'] = 121
n = 3  # dimension of system (and input layer)
num_initial_conditions = 5000  # per training file
params['delta_t'] = 0.05

# settings related to saving results
params['folder_name'] = 'exp3_best'

# settings related to network architecture
params['num_real'] = 0
params['num_complex_pairs'] = 1
params['num_evals'] = 2
k = params['num_evals']  # dimension of y-coordinates
w = 105
params['widths'] = [3, w, k, k, w, 3]
wo = 300
params['hidden_widths_omega'] = [wo, ]

# settings related to loss function
params['num_shifts'] = 30
params['num_shifts_middle'] = params['len_time'] - 1
max_shifts = max(params['num_shifts'], params['num_shifts_middle'])
num_examples = num_initial_conditions * (params['len_time'] - max_shifts)
params['recon_lam'] = .1
params['Linf_lam'] = 10 ** (-7)
params['L1_lam'] = 0.0
params['L2_lam'] = 10 ** (-13)
params['auto_first'] = 1

# settings related to training
params['num_passes_per_file'] = 15 * 6 * 10
params['num_steps_per_batch'] = 2
params['learning_rate'] = 10 ** (-3)
params['batch_size'] = 256
steps_to_see_all = num_examples / params['batch_size']
params['num_steps_per_file_pass'] = (int(steps_to_see_all) + 1) * params['num_steps_per_batch']

# settings related to timing
params['max_time'] = 6 * 60 * 60  # 6 hours
params['min_5min'] = .45
params['min_20min'] = .001
params['min_40min'] = .0005
params['min_1hr'] = .00025
params['min_2hr'] = .00005
params['min_3hr'] = .000005
params['min_4hr'] = .0000007
params['min_halfway'] = 1

for count in range(200):  # loop to do random experiments
    training.main_exp(copy.deepcopy(params))