💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
该文讲解一种基于候选故障频率优化克(IESCFFOgram)的改进包络频谱的特征自适应方法,用于从频谱相干性(SCoh)中识别信息 频谱频段,以进行轴承故障诊断。在新方法中,根据SCoh的局部特征自动识别候选故障频率(CFF),而不是标称故障特性频率(FCF), 并进一步用于指导信息频段的选择。 这种新方法完全摆脱了对FCF或稀疏性指标的依赖,可以通过 挖掘隐藏在SCoh平面中的故障信息,自适应地生成诊断IES。 因此,所提出的IESCFFOgram适用于在没有准确FCF的情况下滚动轴承的故障识别。还提供用于估计光谱相关性(或光谱相干性)的快速算法。
用于检测和分析循环平稳信号。
用于轴承故障诊断的候选故障频率优化与改进包络频谱研究
一、轴承故障诊断的基本原理与核心挑战
-
故障机理与特征频率
轴承故障通常表现为滚动体、保持架、外环或内环的局部损伤,产生周期性冲击信号。这些冲击在振动信号中表现为特征频率(如BPFO、BPFI、FTF、BSF)及其谐波,并伴随边频调制现象。理论故障频率可通过几何参数(滚动体数量、接触角等)计算,但实际应用中因制造误差、负载变化等因素,需在理论值附近搜索近似值。 -
包络频谱的作用与局限性
包络分析通过提取调制信号的低频成分(如Hilbert变换),分离故障特征频率与高频共振成分,是故障诊断的核心工具。但传统包络频谱存在以下问题:- 对噪声敏感,强背景噪声下故障频率可能被淹没;
- 依赖先验知识选择解调频带,人工干预成本高;
- 复杂工况(如变速、多故障耦合)下分辨率不足。
-
候选故障频率(CFFs)的意义
CFFs是基于经验或统计确定的可能故障频率范围,用于缩小诊断目标范围。优化CFFs可减少误检率,提高诊断效率。
二、候选故障频率的优化方法
-
基于统计分析的优化
- 故障数据库驱动:通过历史数据统计不同类型故障的实际特征频率分布,动态调整CFFs范围。例如,内圈故障频率(BPFI)在理论值±10%范围内波动的概率达90%。
- 混合特征融合:结合时域指标(峰度、脉冲因子)与频域指标(谐波能量比),构建加权评分模型筛选CFFs。
-
基于信号处理的优化
- 谱相干性(SCoh)分析:在频谱频率(f)与循环频率(α)的二维平面上,SCoh值高的区域指示潜在故障频率。通过局部极大值检测和能量比量化,自适应生成CFFs,摆脱对标称故障频率(FCF)的依赖。
- 循环平稳性检测:利用二阶循环自相关函数识别周期性冲击,提取具有显著循环平稳特性的频率作为CFFs。
-
智能优化算法
- IESCFFOgram方法:通过1/3二叉树滤波器组分割频带,计算各窄带中CFFs的能量占比,选择最大能量比对应的频带生成诊断谱。该方法在低信噪比(SNR<0 dB)下仍能有效提取故障特征。
- 梯度驱动优化:结合可微分短时傅里叶变换(STFT),通过自动微分技术优化窗口长度,平衡时频分辨率以提升CFFs识别精度。
三、包络频谱的改进技术
-
基于谱相干性(SCoh)的增强方法
- 改进增强包络谱(IEES) :利用光谱基尼指数(SGI)筛选富含故障信息的频带,积分生成高信噪比包络谱。实验表明,IEES在SNR=-5 dB时仍可清晰识别BPFI谐波。
- 加权联合提升包络谱(WCIES) :通过多窄带包络谱的加权融合,整合分散的故障信息,避免单一频带选择偏差。该方法在高铁轴箱轴承诊断中成功提取微弱故障特征。
-
时频分析与自适应解调
- 小波包-AR模型联合去噪:先通过自回归模型去除离散干扰(如齿轮啮合频率),再利用小波包分解选择最优解调频带。韩国航空航天大学数据集验证显示,该方法使故障特征幅值提升3倍。
- 改进经验模态分解(EEMD) :结合Hilbert变换和模态分量筛选,解决传统EMD的模态混叠问题,提升内圈故障诊断准确性。
-
深度学习驱动的包络优化
- 多尺度卷积神经网络(MS-CNN) :使用不同尺寸卷积核提取多尺度包络特征,融合后输入分类网络,实现端到端故障识别,准确率达98.7%。
- 孪生网络小样本诊断:在标记数据有限时,通过改进孪生胶囊网络(Siamese Capsule Network)学习包络谱的相似性,诊断准确率较传统方法提升15%。
四、联合优化技术的实际应用案例
案例1:风电齿轮箱轴承故障诊断(基于IESCFFOgram)
- 信号预处理:采集振动信号后,使用快速SC算法计算SCoh平面,识别候选故障频率(如BPFO≈72 Hz)。
- 频带优化:通过1/3二叉树滤波器组分割频谱,计算各窄带能量比,选择中心频率2.4 kHz、带宽400 Hz的频带生成IES。
- 结果验证:IES中BPFO及其3次谐波清晰可见,幅值较传统包络谱提升2.5倍,成功诊断外圈剥落故障。
案例2:高铁轴箱轴承早期损伤检测(基于WCIES)
- 多传感器融合:同步采集振动与声发射信号,通过时域同步平均抑制轨道冲击噪声。
- 联合优化解调:利用谱相干性确定CFFs(如BSF≈128 Hz),结合加权包络谱提取微弱调制成分,检测到0.2 mm的滚动体划痕。
- 在线监测系统集成:将该方法嵌入车载监测终端,实现故障预警响应时间<10 ms。
五、研究前沿与未来方向
-
复合故障诊断
针对多故障耦合问题,采用三维几何特征稀疏成分分析(TGF-SCA)分离故障源,结合IESFOgram优化频带选择。 -
强电磁干扰(EMI)环境下的诊断
基于改进包络谱阿尔法最大化准则(IESAM),在EMI噪声中提取轴承故障特征,已在直升机主齿轮箱测试中验证有效性。 -
数字孪生与迁移学习
构建轴承物理模型与运行数据的数字映射,通过域适应迁移学习(如Wasserstein距离引导表示学习),实现实验室数据到工业场景的泛化诊断。 -
边缘计算与轻量化模型
开发基于龙舞算法(Dragon Dance Algorithm)的轻量级诊断模型,在嵌入式设备(如STM32H7)上实现实时处理,功耗降低40%。
六、总结
候选故障频率优化与包络频谱改进是提升轴承故障诊断可靠性的关键技术。通过SCoh平面分析、智能频带选择和深度学习增强,新一代方法(如IESCFFOgram、WCIES)显著提升了复杂工况下的诊断精度。未来研究需进一步解决复合故障分离、极端环境适应性问题,并推动算法在工业现场的落地应用。
📚2 运行结果

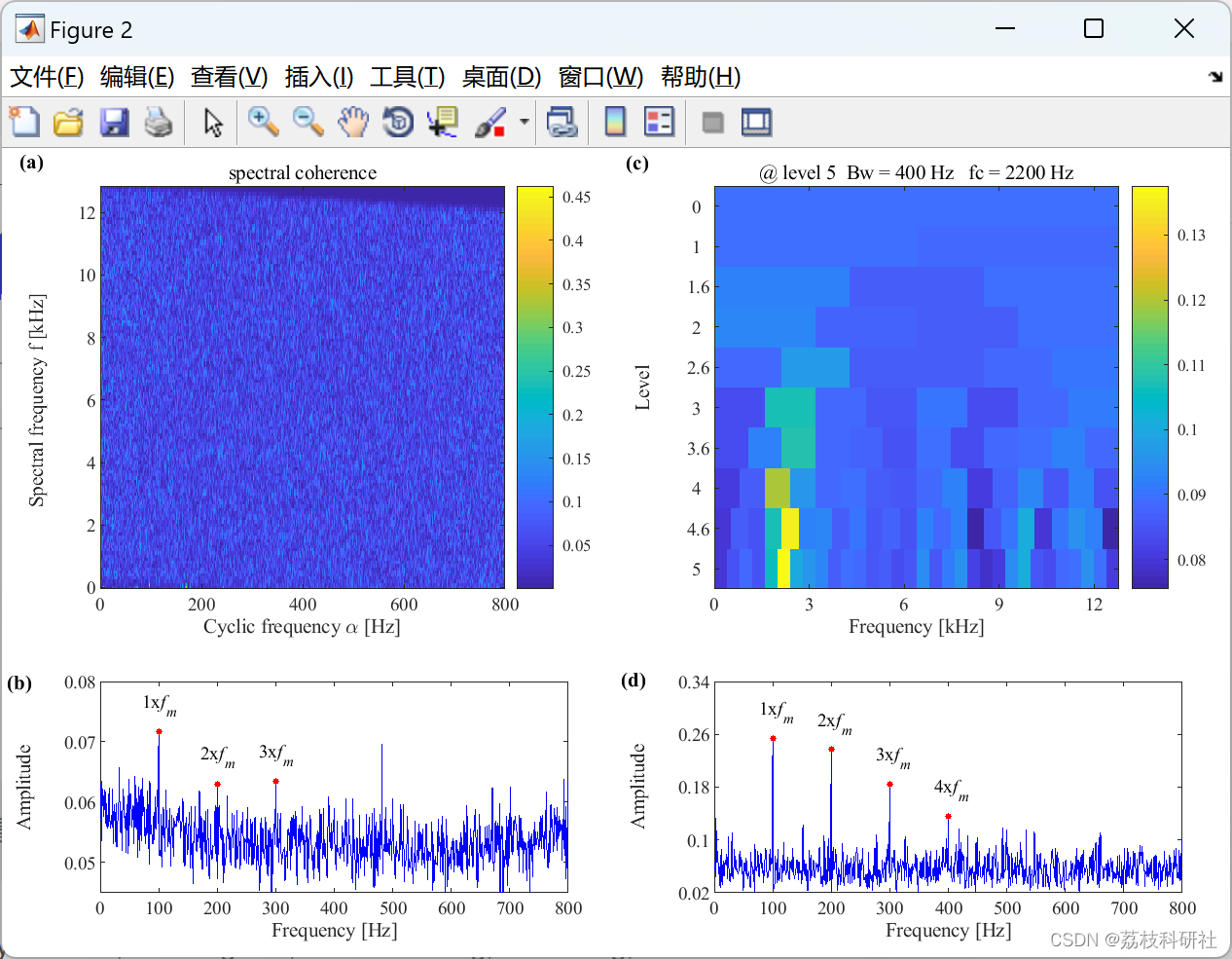



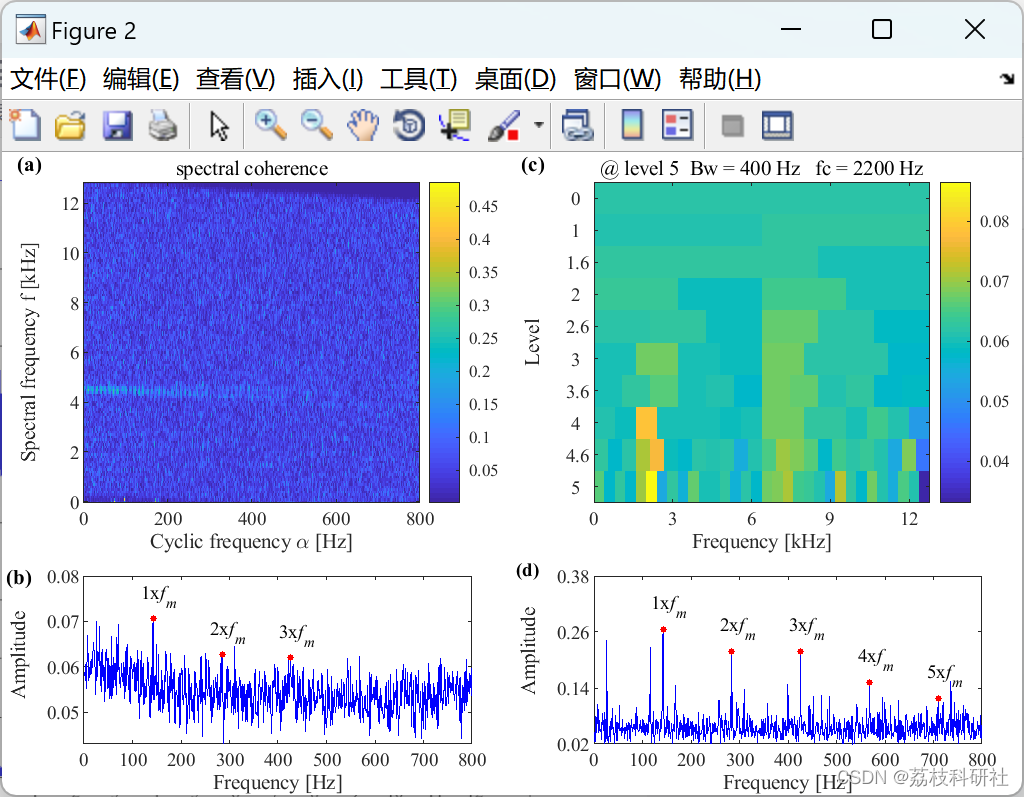
部分代码:
%% Load Simlated Inner race fault signal
load('SimInner');
Sigplot = SimInner;
%% Basic parameters
Fs = 12800*2; % Sampling Frequency
N = 1*Fs ; % Sampling Length
t = 0 : 1/Fs : (N-1)/Fs ; % Time
f_m = 142 ; % Bearing fault charatersitic fraquency
f_shaft = 26;
%% Plot the raw signal components and the frequency spectrum of the mixed signal
% Frequency spectrum of the mixed siganl
nfft = 2*ceil(length(Sigplot(:,5))/2); Freraw = Fs*(0:nfft/2-1)/nfft;
env = Sigplot(:,5);
% env = abs(hilbert(Sigplot(:,5)));
Han = hanning(length(env)); Han = Han(:);
EnvSpec = abs(fft(((env-mean(env)).^1).*Han,nfft));
EnvSpec = EnvSpec./max(EnvSpec);
EnvSpec(nfft/2+1:end) = [];
% Figure
figure(1)
subplotnum_1 = 3;
subplotnum_2 = 2;
leftleave = 0.067;
upleave = 0.005;
downleave = 0.082;
step_1 = (1-0-upleave)/subplotnum_1;
step_2 = 1/subplotnum_2;
plotheight = step_1*0.70;
plotwidth = step_2*0.83;
str = {'(a)','(b)','(c)','(d)','(e)','(f)'};
set (gcf,'unit','centimeters','Position',[12 15 14 8.5], 'color','w'); % 脥录脝卢脦禄脰脙 麓贸脨隆
for i = 1 : subplotnum_1
for j = 1 : subplotnum_2
if (i-1)*2+j <6
plotx = t';
ploty = Sigplot( : , (i-1)*2+j );
else
plotx = Freraw/1000;
ploty = EnvSpec*0.3;
end
subplot(subplotnum_1,subplotnum_2, (i-1)*subplotnum_2+j)
plot( plotx , ploty, 'b' ); % ylabel('Amplitude');
set(gca,'unit','normalized','Position',[leftleave+(j-1)*step_2 downleave+(subplotnum_1-i)*step_1 plotwidth*1 plotheight*1]);
figure_FontSize = 7; set(gca,'Fontsize',figure_FontSize,'Fontname','Times New Roman');
if (i-1)*2+j == 1
set(gca,'ytick',[-1 0 1]); set(gca,'ylim',[-1 1]);
yt = 1;ys = 0;
elseif (i-1)*2+j == 2
set(gca,'ytick',[-2 :2: 2]); set(gca,'ylim',[-2 2]);
yt = 2;ys = 0;
elseif (i-1)*2+j == 3
set(gca,'ytick',[-0.8 0.4 1.6]); set(gca,'ylim',[-0.8 1.6]);
yt = 1.6;ys = 0.4;
elseif (i-1)*2+j == 4
set(gca,'ytick',[-3 0 3]); set(gca,'ylim',[-3 3]);
yt = 3; ys = 0;
elseif (i-1)*2+j == 5
set(gca,'ytick',[-4 0 4]); set(gca,'ylim',[-4 4]);
yt = 4; ys = 0;
elseif (i-1)*2+j == 6
set(gca,'ytick',[0 :0.1 : 0.3]); set(gca,'ylim',[0 0.3]);
yt = 0.3; ys = 0.15;
end
if (i-1)*2+j < 6
set(gca,'xtick',[0: 0.2: 1]); set(gca,'xlim',[0 1]);
xlabel('Time [s]');
ylabel('Amplitude','Position',[-0.10*1 ys]);
xt = -0.15*1;
else
set(gca,'xtick',[0: 1: Fs/2/1000]); set(gca,'xlim',[0 Fs/2/1000]);
xlabel('Frequency [kHz]');
ylabel('Amplitude','Position',[-0.10*Fs/2/1000 ys]);
xt = -0.15*Fs/2/1000;
end
text(xt,yt,str{(i-1)*2+j},'Fontname','Times New Roman','FontSize',8,'FontWeight','bold')
🎉3 参考文献
部分理论来源于网络,如有侵权请联系删除。
[1]Yao Cheng, Shengbo Wang, Bingyan Chen, Guiming Mei, Weihua Zhang, Han Peng, Guangrong Tian, "An Improved Envelope Spectrum via Candidate Fault Frequency Optimization-gram for Bearing Fault Diagnosis", Journal of Sound and Vibration,Elsevier, 2022.
[2]徐秀芳,徐丹妍,徐森,郭乃瑄,许贺洋.一种结合谱聚类与关联规则的轴承故障诊断方法[J].计算机测量与控制,2023,31(01):51-58.DOI:10.16526/j.cnki.11-4762/tp.2023.01.008.























 2603
2603

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








