💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
文献来源:

近年来极端灾害导致电网大停电事故频繁发生[1] ,配电网韧性反映配电系统对灾害的抵御、适应与恢复供电的能力[2] ,受到了广泛关注。此外,为应对能源枯竭和环境污染的双重危机,大量分布式电源(DG)、电能替代负荷接入配电网,为负荷恢复提供了解决方案[3] 。因此,在灾害前后有效利用各类分布式资源以减少停电损失,对提升配电网韧性具有重要意义。
考虑配电网内接入了光伏、移动储能、电动汽车充电桩(EVS)与柴油发电机等分布式资源,电网-交通网融合系统示意结构如图 1 所示。在灾害发生前配电网内负荷由上级主网供电,灾害发生后配电网失去主网供电且出现若干条线路故障,交通网络在灾害负荷恢复期间的实时通行能力受到灾害影响。
目前,国内外学者对利用分布式资源进行灾后恢复进行了广泛研究,主要包括孤岛微电网、应急发
电机与移动资源等方面[4] 。在孤岛微电网方面,文献[5]提出一种利用 DG 和远程控制开关恢复重要负荷的微电网形成机制。文献[6]在主网与配电线路故障时,利用柴油发电(DEG)、固定式储能与光伏(PV)机组恢复负荷。文献[7]提出一种基于计划微电网的负荷恢复方法,在主网供电中断时使负荷削减成本最小。文献[8]提出了考虑负荷分布与燃料型 DG 选址定容的恢复策略,减少了应急电源储备量。上述研究均需要预先配置微电网或大量燃料型电源,投资成本较高且不利于碳减排。

在电网-交通网融合系统中,移动储能的调度状态由其充放电状态和交通运输状态共同决定,具有
时空耦合特性。考虑移动储能 i 在节点 j 与节点 k 间的交通通行时间 T ME i,j,k ( t )与安装配置时间 T0 ME ,建立 移动储能的时空动态调度模型,设运输过程不消耗电能,其时空动态调度如图 2 所示。


面向配电网韧性提升的移动储能预布局与动态调度策略研究
一、配电网韧性的定义与评价指标
-
韧性的多阶段特性
配电网韧性被定义为系统在极端事件(如自然灾害)中表现出的全过程能力,包括:- 灾前:主动感知、预判灾害并优化资源布局(如移动储能)的能力。
- 灾中:抵抗扰动、维持关键负荷供电的鲁棒性。
- 灾后:快速恢复供电的适应性与自愈能力。
美国、欧盟等机构进一步细化了韧性特征,如鲁棒性、机敏性、恢复力和学习力。
-
评价指标与不足
- 静态指标:基于网络拓扑的连通性、中心性等,反映系统结构的抗毁性。
- 动态指标:如恢复供电时间、甩负荷成本、系统性能曲线下的缺失面积(韧性三角形/梯形模型)。
- 现存问题:现有指标多侧重单一阶段,缺乏动态多阶段耦合的评估体系,且对灾害类型(台风、地震等)的针对性不足。
二、移动储能技术的基本原理与应用场景
-
技术原理
- 核心组件:电池组(锂离子为主)、逆变器、控制系统,支持灵活充放电。
- 功能特性:即插即用、快速响应(毫秒级)、可移动部署。
- 容量分类:1度电以下用于小型设备供电,1度电以上支持家庭备电或孤岛运行。
-
应用场景与优势
- 极端事件应对:灾后快速恢复关键负荷供电,替代传统燃油发电机。
- 日常优化:参与电力调峰、电压支撑,降低网损。
- 局限性:储能容量有限、高成本(约0.8-1.5元/Wh),需结合分布式电源协同优化。
三、移动储能预布局方法研究现状
-
鲁棒优化模型
- 两阶段模型:灾前以最恶劣场景(如光伏出力下限)为目标,优化储能配置数量与位置;灾后通过负荷削减和网络重构最小化损失。
- 不确定性建模:采用盒式不确定集合描述光伏出力波动,结合列约束生成(C&CG)算法求解。
-
智能算法应用
- 粒子群算法:用于多目标优化(如最小化网损与电压波动)。
- 遗传算法:解决储能选址定容的非线性问题,提升收敛速度。
四、动态调度策略的典型模型
-
模型预测控制(MPC)
- 滚动优化:结合未来状态预测与实时反馈,实现多时间尺度(小时级)调度。
- 应用场景:风光出力波动下,优化储能充放电与微网运行。
-
随机优化与博弈论
- 场景分析法:蒙特卡洛模拟生成极端事件场景集,评估期望负荷损失。
- 主从博弈:协调电动汽车(V2G模式)与移动储能,实现电价激励下的负荷转移。
五、提升配电网韧性的协同策略
-
灾前-灾后协同优化
- 预布局阶段:通过鲁棒优化确定储能配置,确保灾后快速响应。
- 动态调度阶段:结合网络重构、分布式电源(DG)与储能协同,最大化关键负荷恢复。
-
多能源系统耦合
- 电-气-热互联:利用天然气网冗余性提升供电韧性,降低单一能源依赖。
- 交通网协同:调度电动汽车作为移动储能单元,优化充电站布局与应急供电路径。
六、协同优化案例研究
-
两阶段鲁棒优化模型(华北电力大学案例)
- 灾前布局:采用C&CG算法优化储能配置,降低负荷削减成本15%-20%。
- 灾后恢复:通过移动储能与DG协同,关键负荷恢复率提升至78%。
-
IEEE 33节点仿真验证
- 结果对比:引入移动储能后,系统韧性指标(基于性能曲线面积)从0.572提升至0.776。
- 经济性分析:配置成本增加30%,但总运行成本(含甩负荷损失)降低45%。
七、未来研究方向
- 多灾害类型建模:针对台风、地震等不同灾害特征,开发差异化优化模型。
- 可再生能源深度整合:研究风光出力不确定性与储能调度的耦合机制。
- 标准化指标体系:建立动态多阶段、多属性决策的韧性评估框架。
结论
移动储能通过预布局与动态调度的协同优化,可显著提升配电网在极端事件中的韧性。未来需进一步结合多能源耦合与智能算法,构建标准化评估体系,推动技术在实际工程中的应用。
📚2 运行结果
2.1 灾前预防阶段
灾前预防采用CCG算法,运行一下程序得到的结果如下:

为了更加清晰看到CC&G算法收敛情况以及不确定变量的取值情况,补充一下两个结果图。


通过上述两个结果图看出,程序是两次即完全收敛,第二个图是不确定性分布式光伏出力(仅考虑5个时刻),从图中能够看到光伏除第一个时间点受鲁棒保守度限制为下限外,其他时刻均为上限,而目标为储能配置和负荷削减成本,这样的结果和常理不符,光伏出力越小应该成本会越高,为了进一步验证程序问题,将光伏设置到下限值。


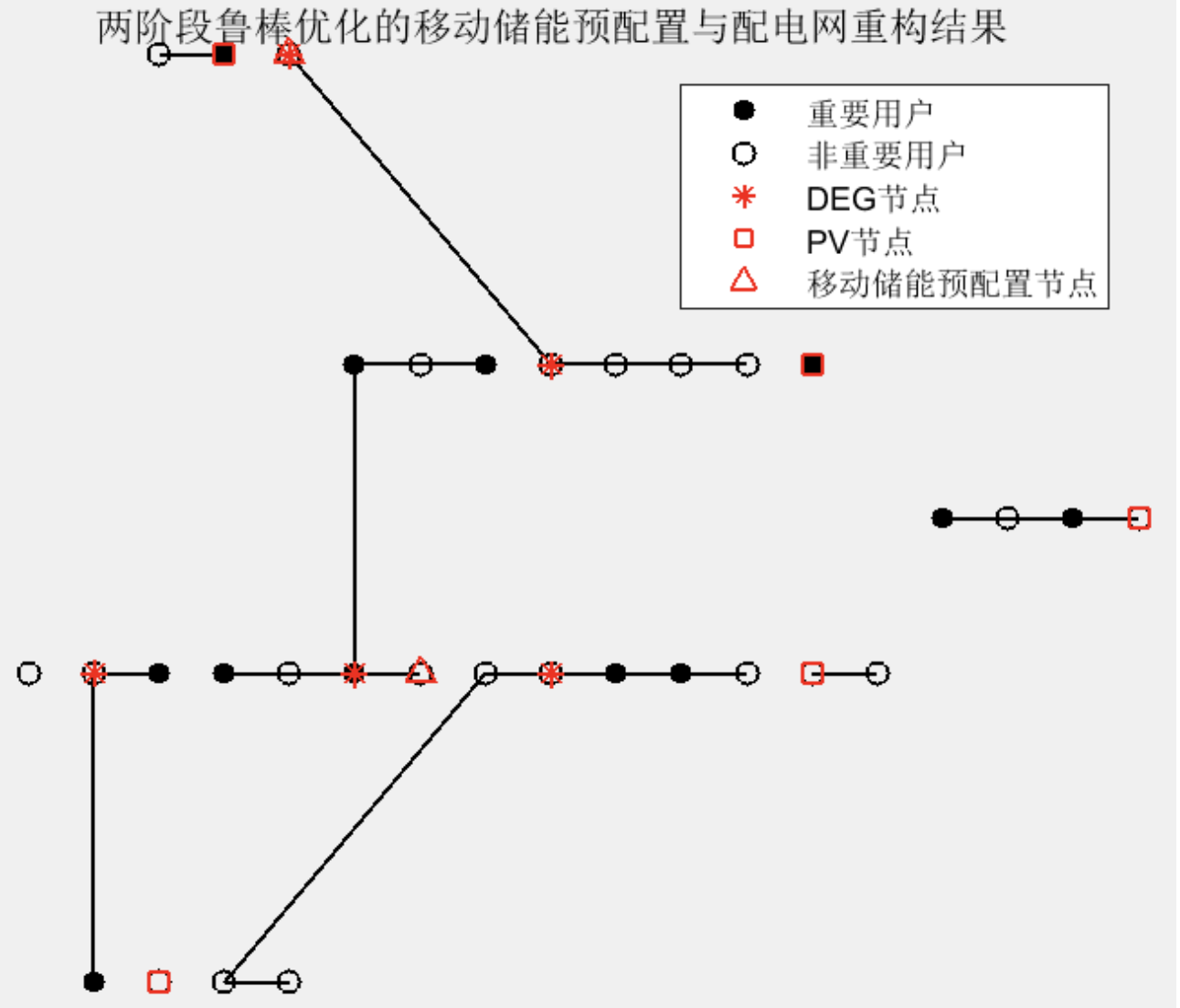
2.2 灾后恢复阶段




部分代码:
clc
close all
%% 表2 移动储能的动态调度结果
alpha_ME1 = value(alpha_ME1);
alpha_ME2 = value(alpha_ME2);
P_Mch = value(P_Mch);
P_Mdch = value(P_Mdch);
for t = 1:NT
disp(['**************' , num2str(O_T(t)) , ':00时刻**************'])
disp(['MESS1接入节点:' , num2str(find(alpha_ME1(:,t))) , ',充放电功率:' , num2str((P_Mdch(1,t) - P_Mch(1,t))*10000) , 'kW'])
disp(['MESS2接入节点:' , num2str(find(alpha_ME2(:,t))) , ',充放电功率:' , num2str((P_Mdch(2,t) - P_Mch(2,t))*10000) , 'kW'])
end
%% 图B3 灾害发生后光伏机组的预测出力
figure
for k = 1:5
if k ~= 4
plot(pv_curve(:,k) , 'linewidth' , 2.5)
hold on
end
end
ylabel('有功功率/kW')
xlabel('时间')
legend('PV1','PV2','PV3、PV4','PV5')
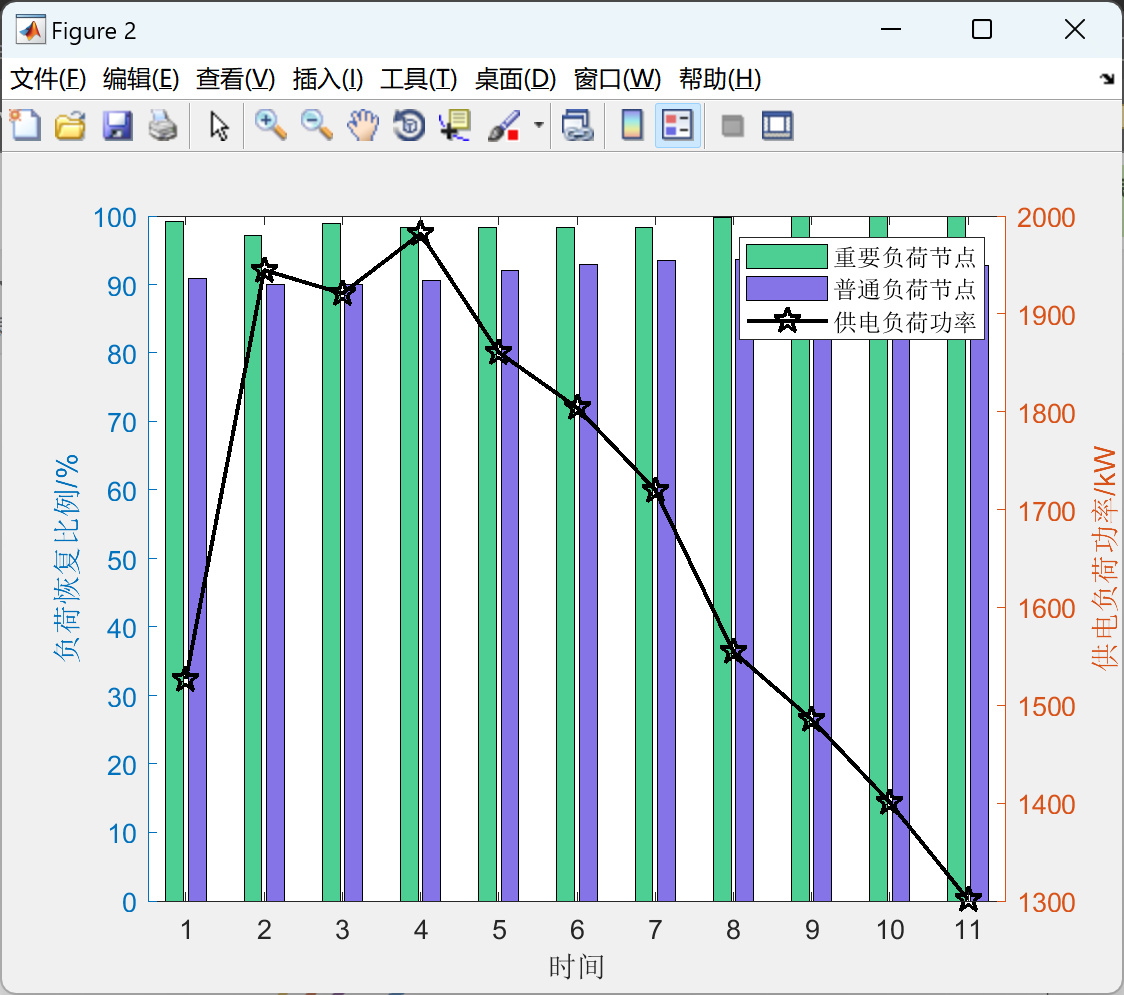
%% 图4 各时段负荷功率和恢复比例
P_Lsu = value(P_Lsu);
essential_load0 = sum(P_L_max(essential_user,:));
ordinary_load0 = sum(P_L_max(ordinary_user,:));
load0 = sum(P_L_max);
essential_load1 = sum(P_L_max(essential_user,:) - P_Lsu(essential_user,:));
ordinary_load1 = sum(P_L_max(ordinary_user,:) - P_Lsu(ordinary_user,:));
load1 = sum(P_Lsu);
figure
yyaxis left
e=bar([essential_load1./essential_load0*100;ordinary_load1./ordinary_load0*100]')
color=[0.300956435005654,0.810590442462569,0.577780697646748;0.521721248782275,0.451274164510932,0.911313227169849;0.561880235062444,0.249969169410276,0.376220283460707;0.241554770085929,0.955437531793689,0.228764772549632;0.912720162652781,0.142650346985794,0.423524871222756;0.825734269699093,0.512563384780399,0.273596220894793;0.444545883918906,0.971925137586938,0.444565843866667;0.982062563214574,0.648320621265659,0.627515046901424;0.578267561462169,0.614671003416509,0.534641253536576;0.234423496393930,0.469650371915959,0.385442159974304];
for i=1:2
set(e(i),'FaceColor',color(i,:));
end
ylabel('负荷恢复比例/%')
hold on
yyaxis right
plot(load1*1000*SB , 'pentagramk-' , 'linewidth' , 1.5 , 'MarkerSize' , 10)
ylabel('供电负荷功率/kW')
legend('重要负荷节点','普通负荷节点','供电负荷功率')
xlabel('时间')
%% 图B4 移动储能有功功率输出与接入位置的关系
figure
yyaxis left
e=bar(P_Mdch'*10000)
color=[0.300956435005654,0.810590442462569,0.577780697646748;0.521721248782275,0.451274164510932,0.911313227169849;0.561880235062444,0.249969169410276,0.376220283460707;0.241554770085929,0.955437531793689,0.228764772549632;0.912720162652781,0.142650346985794,0.423524871222756;0.825734269699093,0.512563384780399,0.273596220894793;0.444545883918906,0.971925137586938,0.444565843866667;0.982062563214574,0.648320621265659,0.627515046901424;0.578267561462169,0.614671003416509,0.534641253536576;0.234423496393930,0.469650371915959,0.385442159974304];
for i=1:2
set(e(i),'FaceColor',color(i,:));
end
hold on
ylabel('有功功率/kW/kW')
yyaxis right
ylabel('节点')
for t = 1:NT
MESS_node1(t) = find(alpha_ME1(:,t));
MESS_node2(t) = find(alpha_ME2(:,t));
end
plot(MESS_node1 , 'bv-' , 'linewidth' , 1)
plot(MESS_node2 , 'ro--' , 'linewidth' , 1)
xlabel('时间')
legend('MESS1放电功率','MESS2放电功率','MESS1接入位置','MESS2接入位置')
%% 图B5 移动储能荷电状态与接入位置的关系
E_ME = value(E_ME);
t0 = [1 2 2 3 3 4 4 5 5 6 6 7 7 8 8 9 9 10 10 11];
E_ME0 = zeros(2,20);
for t = 1:10
E_ME0(1,2*t-1) = E_ME(1,t);
E_ME0(1,2*t) = E_ME(1,t);
E_ME0(2,2*t-1) = E_ME(2,t);
E_ME0(2,2*t) = E_ME(2,t);
end
figure
yyaxis left
plot(t1,E_ME0(1,:)*10000/6 , 'r' , 'linewidth' , 1)
hold on
plot(t1,E_ME0(2,:)*10000/6 , 'b' , 'linewidth' , 1)
ylabel('荷电状态/%')
yyaxis right
ylabel('节点')
for t = 1:NT
MESS_node1(t) = find(alpha_ME1(:,t));
MESS_node2(t) = find(alpha_ME2(:,t));
end
plot(MESS_node1 , 'bv-' , 'linewidth' , 1)
plot(MESS_node2 , 'ro--' , 'linewidth' , 1)
xlabel('时间')
legend('MESS1荷电状态','MESS2荷电状态','MESS1接入位置','MESS2接入位置')
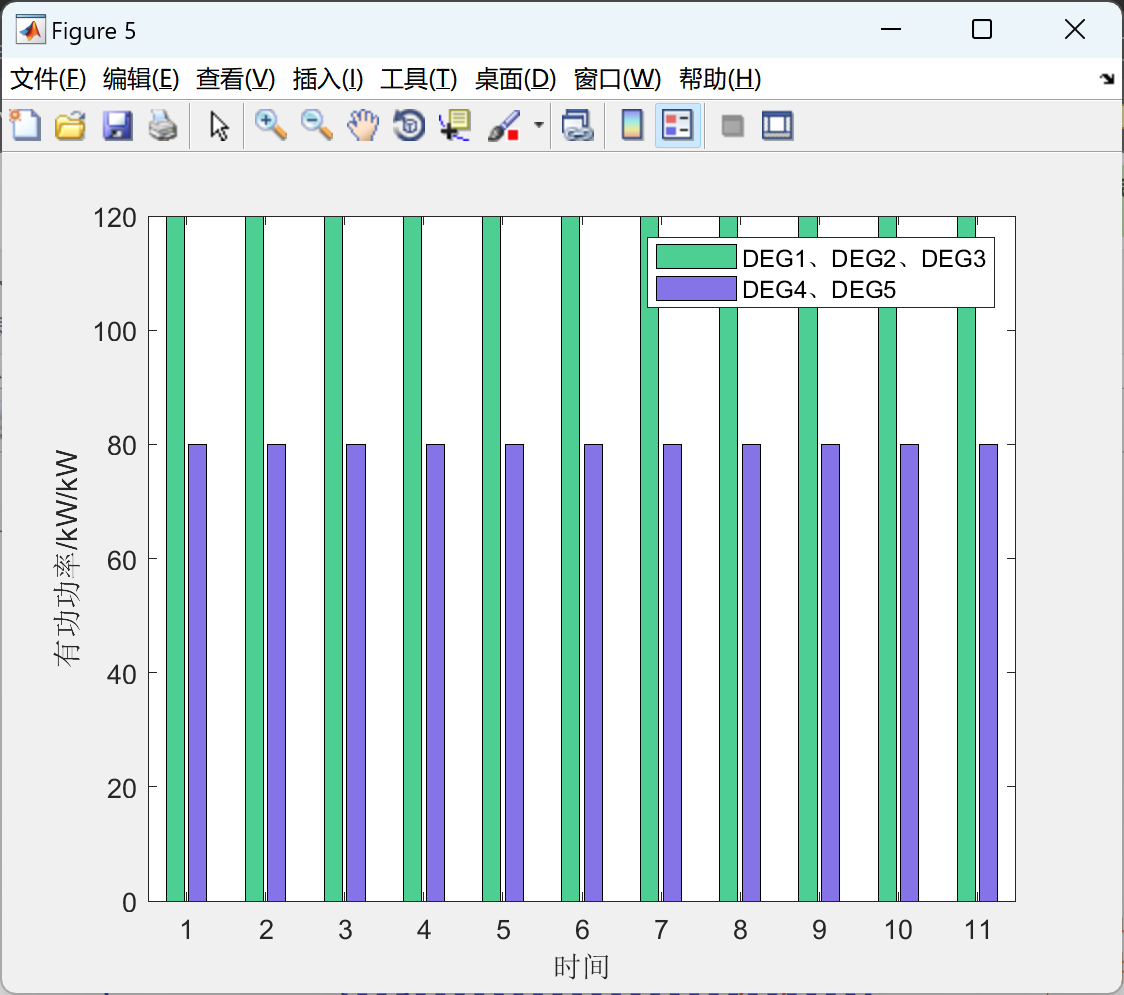
%% 图B6 灾后恢复阶段柴油发电机有功功率输出
figure
P_DG = value(P_DG);
e=bar(P_DG([1,4],:)'*10000)
color=[0.300956435005654,0.810590442462569,0.577780697646748;0.521721248782275,0.451274164510932,0.911313227169849;0.561880235062444,0.249969169410276,0.376220283460707;0.241554770085929,0.955437531793689,0.228764772549632;0.912720162652781,0.142650346985794,0.423524871222756;0.825734269699093,0.512563384780399,0.273596220894793;0.444545883918906,0.971925137586938,0.444565843866667;0.982062563214574,0.648320621265659,0.627515046901424;0.578267561462169,0.614671003416509,0.534641253536576;0.234423496393930,0.469650371915959,0.385442159974304];
for i=1:2
set(e(i),'FaceColor',color(i,:));
end
ylabel('有功功率/kW/kW')
xlabel('时间')
legend('DEG1、DEG2、DEG3','DEG4、DEG5')
%% 图5 各时段电动汽车充电桩的充放电功率
figure
P_Ech = value(P_Ech);
P_Edch = value(P_Edch);
e=bar(P_Edch'*10000 - P_Ech'*10000)
color=[0.300956435005654,0.810590442462569,0.577780697646748;0.521721248782275,0.451274164510932,0.911313227169849;0.561880235062444,0.249969169410276,0.376220283460707;0.241554770085929,0.955437531793689,0.228764772549632;0.912720162652781,0.142650346985794,0.423524871222756;0.825734269699093,0.512563384780399,0.273596220894793;0.444545883918906,0.971925137586938,0.444565843866667;0.982062563214574,0.648320621265659,0.627515046901424;0.578267561462169,0.614671003416509,0.534641253536576;0.234423496393930,0.469650371915959,0.385442159974304];
for i=1:3
set(e(i),'FaceColor',color(i,:));
end
ylabel('有功功率/kW/kW')
xlabel('时间')
legend('EVS1','EVS2','EVS3')
🎉3 参考文献
部分理论来源于网络,如有侵权请联系删除。
[1]王月汉,刘文霞,姚齐等.面向配电网韧性提升的移动储能预布局与动态调度策略[J].电力系统自动化,2022,46(15):37-45.























 2744
2744

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








