【博士论文复现】【阻抗建模、验证扫频法】光伏并网逆变器扫频与稳定性分析(包含锁相环电流环)（Simulink仿真实现）

长安程序猿

于 2025-04-13 08:54:04 发布

阅读量866

点赞数 27

文章标签： matlab

本文链接：https://blog.csdn.net/Yan_she_He/article/details/147186996

版权

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

光伏并网逆变器扫频与稳定性分析（含锁相环、电流环）研究框架

一、阻抗建模基本原理与方法

二、扫频法验证与稳定性判据

三、锁相环（PLL）建模与参数设计

四、电流环控制策略对阻抗特性的影响

五、典型案例与实验验证

六、研究挑战与未来方向

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码、Simulink仿真、文献下载

💥1 概述

并网逆变器序阻抗扫描阻抗建模验证扫频法正负序阻抗包含锁相环电流环。在新能源变流器逆变器阻抗扫描验证方面，我们可以进行逆变器接入弱电网的序阻抗建模与稳定性分析，同时可以设置扫描范围和扫描点数。我们的程序附带详尽的注释，确保每一行都能被轻松理解，包括阻抗建模程序和扫频程序。

文档介绍仿真程序的使用方法。这是我们的升级版本，每次可扫描五个点，实测30个点只需2到5分钟左右。最后，我们还附带Nyquist奈奎斯特曲线绘制结果，为您提供全面的数据支持。

采用序阻抗判定稳定性，理论分析与仿真吻合；

采用考虑电网阻抗影响的电流环路分析（dq阻抗），存在问题：

1）当电网阻抗为10mH时，仿真不稳定，序阻抗判定不稳定，环路分析结果如下。

光伏并网逆变器阻抗建模的基本原理

光伏并网逆变器阻抗建模的基本原理主要包括以下几个方面：

小扰动线性化：阻抗建模的核心是通过小扰动线性化方法，将逆变器和电网视为两个独立子系统，分别建立其阻抗模型。这种方法通常在dq坐标系下进行电压和电流的扰动-响应分析。
谐波线性化：为了简化建模过程，许多研究采用谐波线性化方法。通过在系统中添加谐波扰动信号，利用傅里叶变换提取对应频率分量，在频域中建立线性化传递函数模型。这种方法可以有效减少变量个数，提高建模效率。
状态空间模型：建立并网系统的状态空间模型是阻抗建模的重要步骤。状态空间模型能够描述系统的动态行为，但其计算复杂度较高，因此需要结合现代控制理论进行简化。
锁相环（PLL）的影响：锁相环的动态特性对系统中的坐标变换有重要影响，尤其是在低频段。因此，在建模时需要考虑PLL的动态特性，以确保模型的准确性。
耦合项和电网阻抗：在建模过程中，需要考虑逆变器输出阻抗与电网阻抗的交互作用。通过分析耦合项和电网阻抗的相互影响，可以更准确地描述系统的谐振特性。
稳定性分析：基于奈奎斯特判据等稳定性判据，对建模后的阻抗特性进行分析，以评估系统的稳定性。这一步骤对于设计有效的控制策略至关重要。
仿真验证：通过仿真工具（如PSCAD/EMTDC或MATLAB/Simulink）对建模结果进行验证，确保模型的准确性和有效性。

综上，光伏并网逆变器阻抗建模的基本原理涉及小扰动线性化、谐波线性化、状态空间模型、PLL影响、耦合项和电网阻抗的交互作用以及稳定性分析等多个方面。这些方法和技术共同构成了光伏并网逆变器阻抗建模的基础框架。

扫频法在电力电子系统中的验证方法

扫频法在电力电子系统中的验证方法主要包括以下几个方面：

阻抗建模与验证：扫频法通过改变信号频率并测量电路响应，用于分析电路的特性。阻抗扫描是通过在不同频率点上进行激励响应测试，获得系统的阻抗变化规律。阻抗建模则通过数学模型帮助工程师理解电路特性并进行优化。正负序阻抗和逆变器在阻抗建模中起重要作用，虚拟同步控制（VSG）和逆变器共同作用于模拟实际运行情况下的电路响应，提高阻抗建模的准确性。
虚拟同步发电机（VSG）仿真模型：VSG扫频法通过设置扫描范围和扫描点数，生成系统的阻抗响应曲线，为逆变器的全面评估、虚拟同步控制的有效性验证以及VSG的性能分析和优化提供了基础。程序注释使操作更加便捷，适合无基础用户使用。
直流充电桩测试：基于扫频校准分流器阻值的方法，通过采集电流和电压信号，实时校准分流器阻值，提高测试精度。该方法适用于直流充电桩的有功电能误差试验，并通过延长充电线的结构设计，实现长期运行并测试直流充电桩的有功电能误差。
变压器绕组故障检测：扫频法结合短路阻抗法和频响法，提高了检测灵敏度，能够准确判断变压器绕组变形。该技术已在多个电网的电力变压器抽检中得到应用，并成功检测出变压器绕组变形的情况。
电容电流测量：基于谐振原理的扫频法可用于测量电网对地电容，通过选定电网的一个消弧线圈低压侧进行测量，简单方便。该方法已在实际测试中验证了其准确性。
幅频特性测试：扫频法通过逐一发出特定频率的正弦波，测量待测网络对这些频率信号的幅度响应和相位响应，绘制出幅频特性曲线。该方法广泛应用于科研和生产领域。
仿真验证：扫频法在Simulink仿真环境中用于光伏并网逆变器的序阻抗扫描与稳定性分析，结合锁相环与电流环，是新能源变流器研究的重要手段。

综上，扫频法在电力电子系统中的验证方法涵盖了阻抗建模、虚拟同步控制、直流充电桩测试、变压器故障检测、电容电流测量以及幅频特性测试等多个方面，具有广泛的应用前景和重要的技术价值。

锁相环(PLL)在逆变器中的数学模型及稳定性条件

锁相环（PLL）在逆变器中的数学模型及稳定性条件涉及多个方面，包括PLL的数学模型、传递函数、稳定性分析以及对系统稳定性的影响。以下是基于我搜索到的资料的详细回答：

1. 锁相环（PLL）的数学模型
锁相环是一种闭环控制系统，用于跟踪输入信号的相位和频率。其基本组成包括鉴相器（PD）、低通滤波器（LF）和压控振荡器（VCO）。数学模型通常通过传递函数来描述，具体形式如下：

鉴相器（PD） ：将输入信号与VCO输出信号进行比较，生成相位误差信号。
低通滤波器（LF） ：滤除高频噪声，平滑相位误差信号。
压控振荡器（VCO） ：根据滤波后的相位误差信号调整输出频率和相位。

传递函数可以表示为：

2. 锁相环的传递函数
在逆变器中，PLL的传递函数通常与系统的开环传递函数结合，形成闭环系统。例如，三相并网逆变器的正负序输出阻抗模型中，引入PLL后，等效阻抗会增加一个额外的阻抗。具体传递函数可以表示为：

3. 稳定性条件
锁相环的稳定性条件主要依赖于其传递函数的极点分布。根据李雅普诺夫能量函数分析，PLL的稳定性条件可以总结为以下几点：

极点位于左半复平面：这是系统稳定的必要条件。
闭环传递函数的增益和相位裕度：增益裕度和相位裕度应满足一定的约束条件，以确保系统的鲁棒性和稳定性。

4. 锁相环对系统稳定性的影响
锁相环在逆变器中的作用不仅限于同步电网电压，还对系统的阻抗特性和稳定性有重要影响。例如：

阻抗特性：引入PLL后，逆变器的输出阻抗会增加一个额外的阻抗，这会影响系统的低频特性。
低频特性：PLL的带宽越大，系统的低频振荡频率越高，但稳定性裕度越低。
参考电流的影响：参考电流越大，系统控制裕度越低，稳定性越差。

5. 实际应用中的优化
为了提高PLL在逆变器中的性能，研究者提出了多种优化方法：

参数优化：通过建立PLL参数之间的数学关系，优化开环传递函数，提高系统的动态性能和稳定性。
滤波器设计：在传统PLL中加入低通滤波器（LPF），以降低PLL对系统稳定性的影响。
改进算法：如基于二阶双广义积分器的SOGI-PLL，能够更好地适应弱电网条件。

6. 结论
锁相环在逆变器中的数学模型和稳定性条件涉及其传递函数、极点分布、阻抗特性和参考电流等多个方面。通过优化PLL参数和设计改进算法，可以显著提高逆变器在弱电网条件下的稳定性和鲁棒性。

光伏并网逆变器扫频与稳定性分析（含锁相环、电流环）研究框架

一、阻抗建模基本原理与方法

建模理论基础
阻抗分析法将系统分解为逆变器阻抗ZinvZinv与电网阻抗ZgridZgrid两个子系统，通过奈奎斯特判据分析交互稳定性。核心步骤包括：
- 小信号线性化：在dq坐标系下对非线性系统进行扰动-响应分析，推导导纳矩阵。
- 锁相环（PLL）建模：PLL动态特性显著影响低频段阻抗特性，需在模型中引入其闭环传递函数HPLL(s)HPLL(s)。
- 滤波器类型影响：L型与LCL型滤波器需分别推导导纳矩阵，LCL型需考虑谐振点抑制策略。
关键改进方向
- 频率耦合效应：谐波线性化方法通过注入电压扰动并提取频域响应，可准确表征正/负序阻抗矩阵的非对称特性。
- 多机并联聚合模型：等效导纳需考虑线路阻抗叠加效应，需推导定电流控制下的小信号模型及导纳聚合公式。
典型阻抗模型表达式
考虑PLL的三相逆变器输出阻抗可表示为：

二、扫频法验证与稳定性判据

扫频法实施步骤
- 频率范围设置：覆盖0.1Hz至数kHz（如2kHz），重点分析PLL带宽内（典型值10-100Hz）的负阻抗特性。
- 扰动注入方式：通过电压源注入谐波扰动，测量电流响应，利用FFT提取频域导纳数据。
- 数据后处理：计算正/负序阻抗比Zinv/ZgridZinv/Zgrid，绘制奈奎斯特曲线，判断包围点(-1,j0)的情况。
稳定性判据扩展
- 多输入多输出系统：需将MIMO阻抗矩阵转换为SISO等效模型，利用广义奈奎斯特判据分析相位裕度。
- 弱电网条件：电网阻抗ZgridZgrid增大时，需验证电流环带宽是否足够抑制低频振荡（如10Hz以下）。

三、锁相环（PLL）建模与参数设计

PLL数学模型
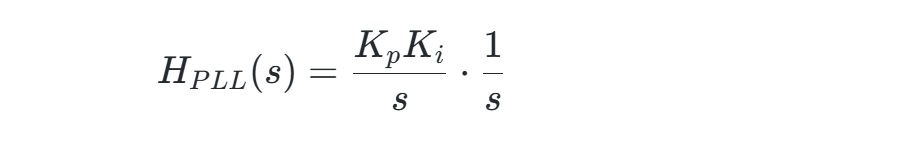
- SRF-PLL结构：包含鉴相器（PI控制器）、积分环节及坐标变换，传递函数为：

带宽设计需平衡动态响应与稳定性。

DSOGI-FLL改进：采用双二阶广义积分器，增强抗电网谐波干扰能力，传递函数含阻尼因数kk与角频率ωFLL。

参数优化准则
- 带宽限制：PLL带宽fbwfbw应小于电网基频的1/10（如5Hz），避免引入负阻尼。
- 相位裕度：通过调整PI参数，使开环传递函数在穿越频率处相位裕度≥45°。

四、电流环控制策略对阻抗特性的影响

控制结构分析
- 虚拟阻抗法：在电流环中引入虚拟电阻RvRv和电感LvLv，重塑输出阻抗特性，抑制谐振。
- 有源阻尼设计：电容电流反馈控制通过调节系数KdKd，抑制LCL滤波器谐振峰，表达式为：

其中ωrωr为谐振频率。

参数敏感性与稳定性
- 比例系数KpKp：增大KpKp可提升电流环带宽，但可能导致高频段阻抗负阻尼。
- 延时效应：控制链路延时超过100μs时，需采用多速率采样或前馈补偿，避免相位滞后引发振荡。

五、典型案例与实验验证

Simulink仿真流程
- 步骤1：搭建含PLL和电流环的LCL型逆变器模型，设置扫频参数（如0.1-2000Hz，200点）。
- 步骤2：注入扰动信号，采集V/I数据，通过FFT计算导纳矩阵。
- 步骤3：对比理论阻抗曲线与实测结果，验证模型精度（误差<5%为合格）。
现场实测案例
- 科华数能实证：在宁夏光伏电站完成全工况扫频，通过阻抗重塑将系统谐振点从1.2kHz移至安全区域，验证宽频抑制策略有效性。
- 弱电网适应性：当电网阻抗Lg=10mHLg=10mH时，通过增加电流环KpKp使相位裕度从30°提升至60%，消除低频振荡。

六、研究挑战与未来方向

高频耦合问题
在数kHz以上频段，开关噪声与寄生参数影响显著，需结合电磁兼容（EMC）模型优化。
多时间尺度交互
锁相环（ms级）与电流环（μs级）的协同需设计分层控制策略，避免动态冲突。
人工智能辅助
基于机器学习的参数自适应调优可解决多变量耦合问题，如深度强化学习用于PLL带宽动态调整。

结论：光伏并网逆变器的稳定性分析需综合阻抗建模、扫频验证及控制策略优化。锁相环与电流环的协同设计是确保弱电网适应性的关键，未来需进一步探索高频特性与智能控制方法的融合。

📚2 运行结果

部分代码：

%% 读取FFTscope数据
n=fc0(x)+1;
FFTread;

%% 正负序阻抗计算
Zp_scan=-Vaj/Iaj;%三相对称情况下，A相即为正序分量
GM_Zp_scan_1(x)=GM(Zp_scan);
PM_Zp_scan_1(x)=PM(Zp_scan);
end

%% 绘图
figure(1)
subplot(2,1,1)
% semilogx(fc0,GM_Zp_scan_1,'r+','linewidth',1);hold on;
semilogx(fc0,GM_Zp_scan_1,'bo','linewidth',1.5);hold on;
subplot(2,1,2)
% semilogx(fc0,PM_Zp_scan_1,'r+','linewidth',1);hold on;
semilogx(fc0,PM_Zp_scan_1,'bo','linewidth',1.5);hold on;