【EKF、EPF、UKF、PF、EPF、UPF】【改进粒子滤波算法】粒子滤波EKF、扩展粒子滤波EPF和无迹粒子滤波UPF等比较、并分析了这些算法在提高滤波精度和效率方面的优势（Matlab代码实现）

长安程序猿

于 2025-05-27 10:11:50 发布

阅读量618

点赞数 21

文章标签：算法 matlab 开发语言

本文链接：https://blog.csdn.net/Yan_she_He/article/details/148251665

版权

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

⛳️赠与读者

💥1 概述

非线性滤波算法比较与分析：EKF、EPF、UKF、PF、UPF的精度与效率研究

一、算法基础与核心思想对比

二、滤波精度对比分析

三、计算效率对比分析

四、改进方向与前沿研究

五、综合选型建议

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码实现

⛳️赠与读者

👨‍💻做科研，涉及到一个深在的思想系统，需要科研者逻辑缜密，踏实认真，但是不能只是努力，很多时候借力比努力更重要，然后还要有仰望星空的创新点和启发点。建议读者按目录次序逐一浏览，免得骤然跌入幽暗的迷宫找不到来时的路，它不足为你揭示全部问题的答案，但若能解答你胸中升起的一朵朵疑云，也未尝不会酿成晚霞斑斓的别一番景致，万一它给你带来了一场精神世界的苦雨，那就借机洗刷一下原来存放在那儿的“躺平”上的尘埃吧。

或许，雨过云收，神驰的天地更清朗.......🔎🔎🔎

💥1 概述

非线性滤波算法比较与分析：EKF、EPF、UKF、PF、UPF的精度与效率研究

一、算法基础与核心思想对比

扩展卡尔曼滤波（EKF）
- 原理：通过一阶泰勒展开对非线性系统进行局部线性化，保留标准卡尔曼滤波框架（预测-更新）。
- 适用场景：轻度非线性系统（如机器人定位、电池SOC估计）。
- 优点：计算效率高，实时性强；在参数调整合理时精度可靠。
- 局限性：

线性化误差导致强非线性下精度下降；
对噪声协方差矩阵敏感，需手动调参。

无迹卡尔曼滤波（UKF）
- 原理：基于无迹变换（UT），通过确定性采样sigma点近似非线性分布的高阶矩（均值和协方差）。
- 适用场景：中强度非线性系统（如目标跟踪、飞行器导航）。
- 优点：

无需计算雅可比矩阵，避免线性化误差；
精度可达三阶泰勒展开，优于EKF。
- 局限性：
计算量略高于EKF（但同数量级）；
极强非线性下仍可能发散。

标准粒子滤波（PF）
- 原理：基于蒙特卡洛方法，用带权重的粒子群近似后验概率分布。
- 适用场景：高度非线性、非高斯系统（如复杂环境下的SLAM、故障诊断）。
- 优点：无模型线性化假设，理论上可逼近任意分布。
- 局限性：

粒子退化与贫化问题；
计算复杂度随维度指数增长。

扩展粒子滤波（EPF）
- 改进点：将EKF作为重要性密度函数，更新粒子以融入最新观测信息。
- 优势：

缓解粒子退化，提高采样质量；
在锂电池SOC估计中，误差降低至2%以内。
- 代价：每个粒子需EKF计算，效率低于PF。

无迹粒子滤波（UPF）
- 改进点：结合UKF与PF，利用UKF生成重要性密度函数指导粒子采样。
- 优势：

解决PF的粒子退化问题；
在动态噪声和非高斯环境下精度优于EKF、UKF。
- 代价：计算复杂度最高，需平衡粒子数与实时性。

二、滤波精度对比分析

算法	精度优势	精度劣势	典型应用案例
EKF	轻度非线性下效率与精度均衡	强非线性下线性化误差显著	机器人定位（误差<5%）
UKF	中强度非线性下精度优于EKF（误差降低30%-50%）	极端非线性下发散风险	高空气象目标跟踪（RMSE降低40%）
PF	非高斯、强非线性系统适应性最强	粒子数不足时估计偏差大	复杂SLAM（精度依赖粒子数）
EPF	通过EKF优化粒子分布，SOC估计误差<2%	计算量高于PF	锂电池多工况SOC估计
UPF	动态噪声下精度最优（SOC误差<1.5%）	实时性差，需硬件加速	车载电池动态工况

关键结论：

非线性强度决定算法选择：EKF（轻度）→ UKF（中度）→ PF/EPF/UPF（重度）。
UPF综合最优但代价高：在电池SOC估计中，UPF比EKF精度提升50%以上，但计算时间增加2-3倍。

三、计算效率对比分析

算法	时间复杂度	空间复杂度	优化方向
EKF	O(n²)（n为状态维数）	O(n²)	并行化、参数自适应
UKF	O(n³)（2n+1个sigma点）	O(n²)	简化sigma点生成
PF	O(N·n²)（N为粒子数）	O(N·n)	粒子数自适应
EPF	O(N·n³)（每个粒子需EKF计算）	O(N·n²)	重要性密度简化
UPF	O(N·n³)（每个粒子需UKF计算）	O(N·n²)	混合采样策略

效率权衡案例：

在SINS/GPS/CNS组合导航中，PF精度比EKF高15%，但计算时间增加80%。
UKF在雷达跟踪中与EKF耗时相当，但精度提升30%。

四、改进方向与前沿研究

EKF的优化：
- 变分贝叶斯EKF（VB-EKF）：动态估计噪声协方差，提升鲁棒性。
PF的改进：
- 重采样策略：遗传算法优化粒子多样性（UGPF算法误差降低60%）。
- 混合模型：Rao-Blackwellized PF降低状态空间维度。
UPF的扩展：
- 新息加权自适应UPF：引入噪声协方差在线调整，进一步抑制发散。

五、综合选型建议

场景特征	推荐算法	理由
实时性要求高，轻度非线性	EKF	效率最优，调参简单
中强度非线性，需平衡精度与效率	UKF	无需求导，精度可靠
强非线性、非高斯，离线处理	PF/EPF	理论最优，容忍计算延迟
极端噪声环境，精度优先	UPF	抗噪声能力强，支持动态调整

📚2 运行结果

主函数代码：

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 功能说明：ekf,ukf,pf,epf,upf算法的综合比较程序
function main
% 因为本程序涉及太多的随机数，下面让随机数每次都不变
rng(1);
T = 50; %仿真时间步数
R = 1e-5; %测量噪声
% 产生均值为g1/g2，方差为g1/(g2*g2)
g1 = 3; %Gamma 分布参数，用于产生过程噪声
g2 = 2; %Gamma 分布参数，用于产生过程噪声
% 系统初始化
X = zeros(1,T);
Z = zeros(1,T);
processNoise = zeros(T,1);
measureNoise = zeros(T,1);
X(1) = 1; %状态初值
P0 = 3/4;
% EKF 滤波算法
Qekf=10*3/4; %EKF过程噪声方差
Rekf=1e-1; %EKF过程噪声方差
Xekf=zeros(1,T); %滤波状态
Pekf = P0*ones(1,T); %协方差
Tekf=zeros(1,T); %用于记录一个采样周期的算法时间消耗
% UKF 滤波算法
Qukf=2*3/4; %UKF过程噪声方差
Rukf=1e-1; %UKF过程噪声方差
Xukf=zeros(1,T); %滤波状态
Pukf = P0*ones(1,T); %协方差
Tukf=zeros(1,T); %用于记录一个采样周期的算法时间消耗
% 基本粒子滤波器设置
N=200; %粒子数
Xpf=zeros(1,T); %滤波状态
Xpfset=ones(T,N); %粒子集合初始化
Tpf=zeros(1,T); %用于记录一个采样周期的算法时间消耗
% EPF 滤波器设置
Xepf=zeros(1,T); %滤波状态
Xepfset=ones(T,N); %粒子集合初始化
Pepf = P0*ones(T,N); %各个粒子的协方差
Tepf=zeros(1,T); %用于记录一个采样周期的算法时间消耗
% UPF 滤波器设置
Xupf=zeros(1,T); %滤波状态
Xupfset=ones(T,N); %粒子集合初始化
Pupf = P0*ones(T,N); %各个粒子的协方差
Tupf=zeros(1,T); %用于记录一个采样周期的算法时间消耗
% 以下是模拟系统运行
for t=2:T
processNoise(t) = gengamma(g1,g2); %产生过程噪声
measureNoise(t) = sqrt(R)*randn; %产生观测噪声
% 模拟系统状态运行一步
X(t) = ffun(X(t-1),t) +processNoise(t);
% 模拟传感器对系统观测(测量)一次
Z(t) = hfun(X(t),t) + measureNoise(t);
% 调用 EKF 算法
tic
[Xekf(t),Pekf(t)]=ekf(Xekf(t-1),Z(t),Pekf(t-1),t,Qekf,Rekf);
Tekf(t)=toc;
% 调用 UKF 算法
tic
[Xukf(t),Pukf(t)]=ukf(Xukf(t-1),Z(t),Pukf(t-1),Qukf,Rukf,t);
Tukf(t)=toc;
% 调用 PF 算法
tic
[Xpf(t),Xpfset(t,:)]=pf(Xpfset(t-1,:),Z(t),N,t,R,g1,g2);
Tpf(t)=toc;
% 调用 EPF 算法
tic
[Xepf(t),Xepfset(t,:),Pepf(t,:)]=epf(Xepfset(t-1,:),Z(t),t,Pepf(t-1,:),N,R,Qekf,Rekf,g1,g2);
Tepf(t)=toc;
% 调用 UPF 算法
tic
[Xupf(t),Xupfset(t,:),Pupf(t,:)]=upf(Xupfset(t-1,:),Z(t),t,Pupf(t-1,:),N,R,Qukf,Rukf,g1,g2);
Tupf(t)=toc;
end
% 数据分析、偏差比较
ErrorEkf=abs(Xekf-X); %ekf 算法估计得到的状态与真实状态之间的偏差
ErrorUkf=abs(Xukf-X); %ukf 算法估计得到的状态与真实状态之间的偏差
ErrorPf=abs(Xpf-X); %pf 算法估计得到的状态与真实状态之间的偏差
ErrorEpf=abs(Xepf-X); %epf 算法估计得到的状态与真实状态之间的偏差
ErrorUpf=abs(Xupf-X); %upf 算法估计得到的状态与真实状态之间的偏差
% 画图
figure
hold on;box on;
p1=plot(1:T,X,'-k.','lineWidth',2);
p2=plot(1:T,Xekf,'m:','lineWidth',2);
p3=plot(1:T,Xukf,'--','lineWidth',2);
p4=plot(1:T,Xpf,'-ro','lineWidth',2);
p5=plot(1:T,Xepf,'-g*','lineWidth',2);
p6=plot(1:T,Xupf,'-b^','lineWidth',2);
legend([p1,p2,p3,p4,p5,p6],'真实状态','EKF估计','UKF估计','PF估计','EPF估计','UPF估计')
xlabel('时间');ylabel('状态值');
title('系统状态图')
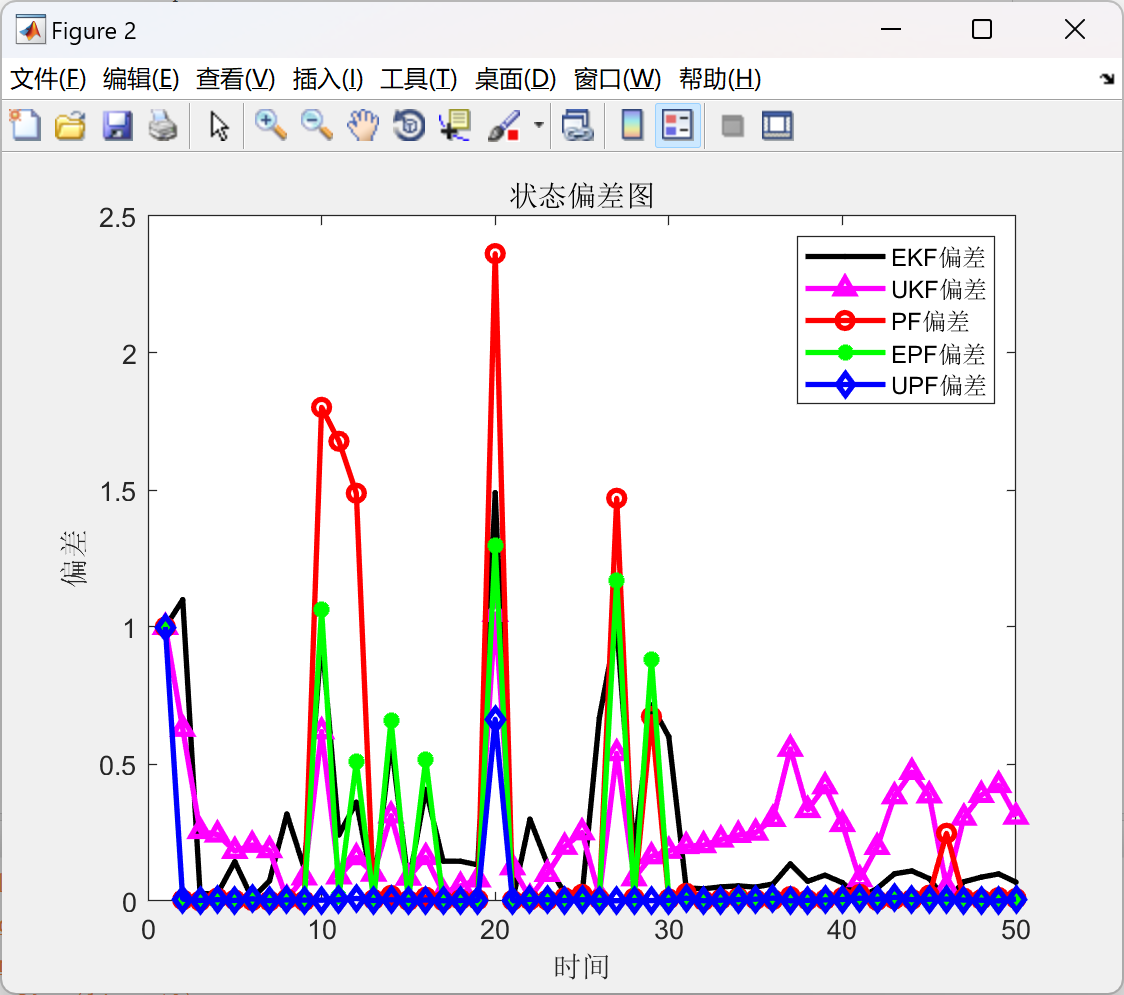
% 偏差比较图
figure
hold on;box on;
p1=plot(1:T,ErrorEkf,'-k.','lineWidth',2);
p2=plot(1:T,ErrorUkf,'-m^','lineWidth',2);
p3=plot(1:T,ErrorPf,'-ro','lineWidth',2);
p4=plot(1:T,ErrorEpf,'-g*','lineWidth',2);
p5=plot(1:T,ErrorUpf,'-bd','lineWidth',2);
legend([p1,p2,p3,p4,p5],'EKF偏差','UKF偏差','PF偏差','EPF偏差','UPF偏差')
xlabel('时间');ylabel('偏差');
title('状态偏差图');
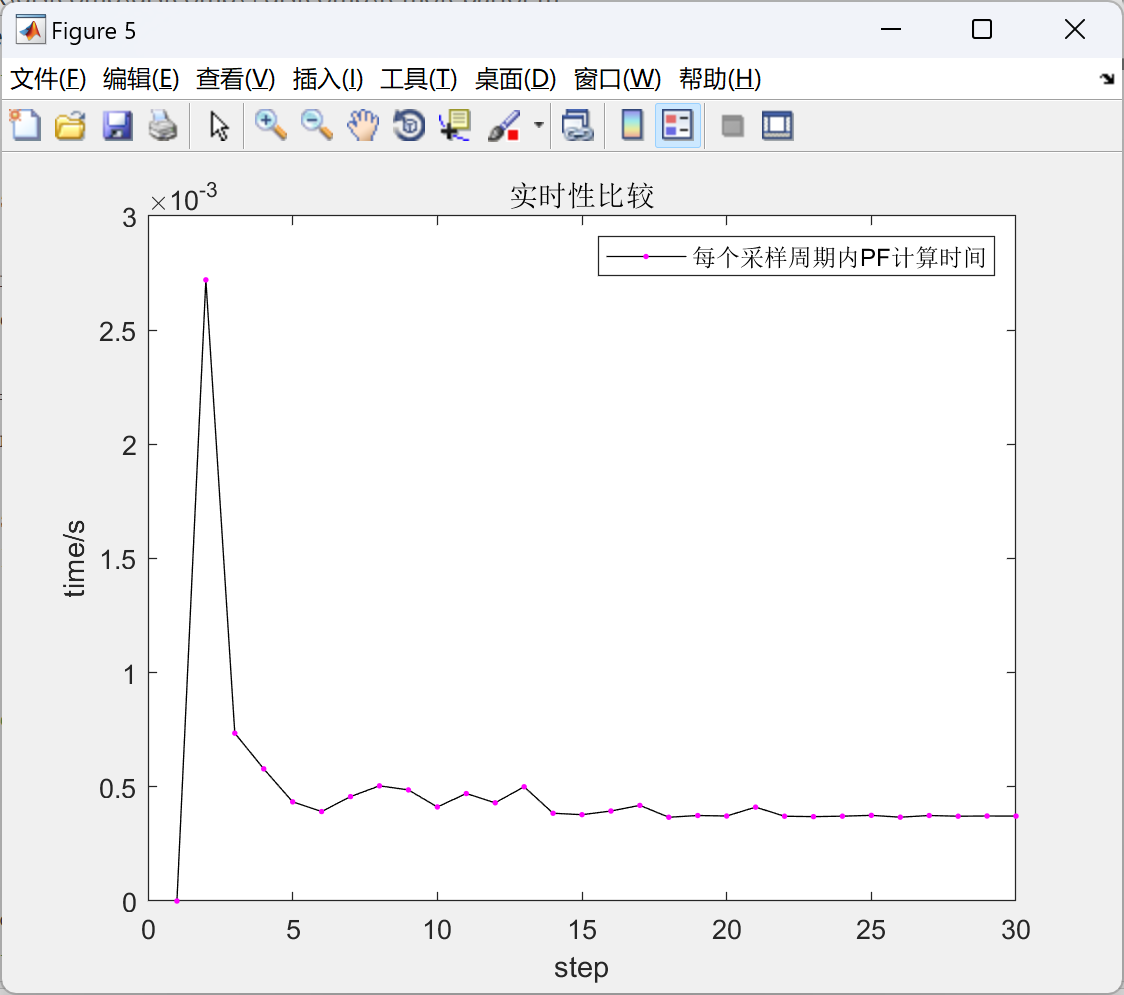
% 算法实时性比较图
figure
hold on;box on;
p1=plot(1:T,Tekf,'-k.','lineWidth',2);
p2=plot(1:T,Tukf,'-m^','lineWidth',2);
p3=plot(1:T,Tpf,'-ro','lineWidth',2);
p4=plot(1:T,Tepf,'-g*','lineWidth',2);
p5=plot(1:T,Tupf,'-bd','lineWidth',2);
legend([p1,p2,p3,p4,p5],'EKF时间','UKF时间','PF时间','EPF时间','UPF时间')
xlabel('时间');ylabel('计算时间');
title('实时性比较');
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%