马尔可夫不等式把概率关联到数学期望,给出了随机变量的累积分布函数一个宽泛但仍有用的界。
定义
马尔可夫不等式用于估计尾事件的概率上界。
- 若随机变量 X X X只取非负值,则 ∀ a > 0 \forall a>0 ∀a>0有:
P ( X ≥ a ) ≤ E ( X ) a \mathbb{P}(X \geq a) \leq \frac{\mathbb{E}(X)}{a} P(X≥a)≤aE(X)
证明
思路1
放大概率,得到部分函数期望
截断函数期望,二者相比较
- 考虑 X ≥ a X\ge a X≥a的情况 → X a ≥ 1 \frac {X}{a} \ge 1 aX≥1
- 对于不等式左边有:
P ( X ≥ a ) = ∫ a + ∞ f ( x ) d x ≤ ∫ a + ∞ X a f ( x ) d x \mathbb P(X \geq a)=\int_{a}^{+\infty} f(x) d x \leq \int_{a}^{+\infty} \frac{X}{a} f(x) d x P(X≥a)=∫a+∞f(x)dx≤∫a+∞aXf(x)dx
- 对于不等式右边有:
E ( X a ) = ∫ − ∞ a X a f ( x ) d x + ∫ a + ∞ X a f ( x ) d x E\left(\frac{X}{a}\right)=\int_{-\infty}^{a} \frac{X}{a} f(x) d x+\int_{a}^{+\infty} \frac{X}{a} f(x) d x E(aX)=∫−∞aaXf(x)dx+∫a+∞aXf(x)dx
- 由于:
∫ − ∞ a X a f ( x ) d x ≥ 0 \int_{-\infty}^{a} \frac{X}{a} f(x) d x \geq 0 ∫−∞aaXf(x)dx≥0
- 因此:
P ( X ≥ a ) ≤ ∫ a + ∞ X a f ( x ) d x ≤ E ( X a ) \mathbb P(X \geq a) \leq \int_{a}^{+\infty} \frac{X}{a} f(x) d x \leq E\left(\frac{X}{a}\right) P(X≥a)≤∫a+∞aXf(x)dx≤E(aX)
- 即:
P ( X ≥ a ) ≤ E ( X a ) = E ( X ) a \mathbb P(X \geq a) \leq E\left(\frac{X}{a}\right)=\frac{E(X)}{a} P(X≥a)≤E(aX)=aE(X)
思路2
原始期望大于截断部分非负值的期望
求取期望时缩小 X X X得到 a a a
E ( X ) = ∫ − ∞ ∞ x f ( x ) d x ≥ ∫ a ∞ x f ( x ) d x ( a ≥ 0 ) ≥ ∫ a ∞ a f ( x ) d x = a ∫ a ∞ f ( x ) d x = a P ( X ≥ a ) \begin{aligned} \mathbb{E}(X) &=\int_{-\infty}^{\infty} x f(x) d x \\ & \geq \int_{a}^{\infty} x f(x) d x \quad(a \geq 0) \\ & \geq \int_{a}^{\infty} a f(x) d x \\ &=a \int_{a}^{\infty} f(x) d x \\ &=a \mathbb{P}(X \geq a) \end{aligned} E(X)=∫−∞∞xf(x)dx≥∫a∞xf(x)dx(a≥0)≥∫a∞af(x)dx=a∫a∞f(x)dx=aP(X≥a)
图示
a a a越大于均值, X > a X>a X>a的概率越小
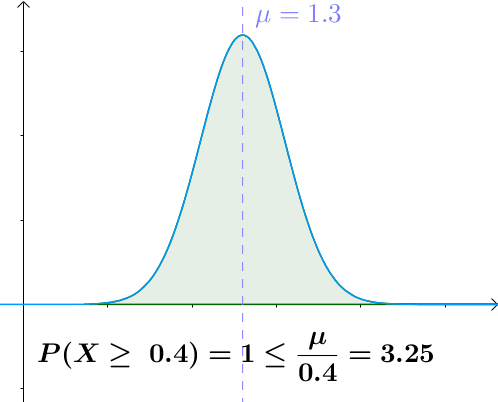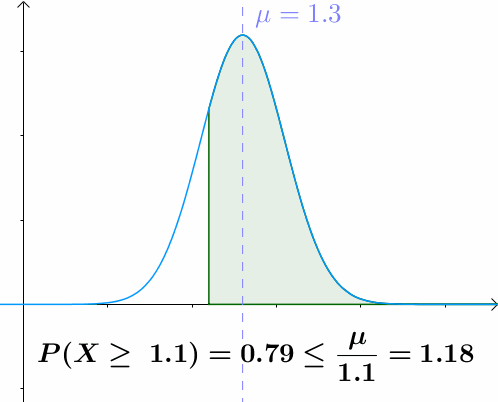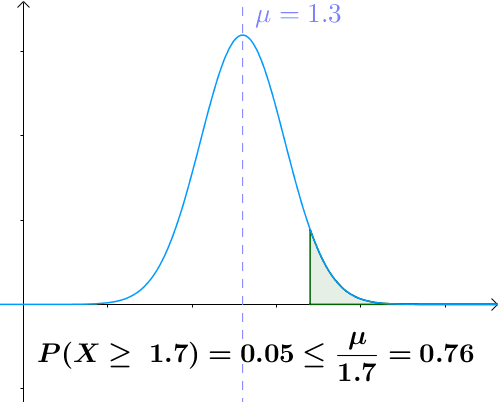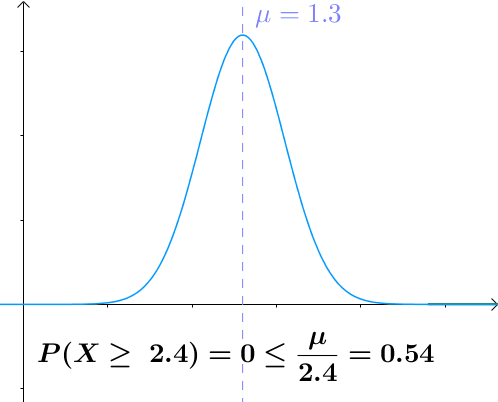
用途
- 将概率与期望联系起来建立了不等式关系
- 约束较松,可以用来粗略估计尾部事件
例如:
如果 X X X是工资,那么 E ( X ) E(X) E(X)就是平均工资,假设 a = n E ( X ) a=n E(X) a=nE(X),即平均工资的 n n n倍。那么根据马尔可夫不等式,不超过 1 / n 1/n 1/n的人会有超过平均工资的 n n n倍的工资。
参考资料
-
https://baike.baidu.com/item/%E9%A9%AC%E5%B0%94%E5%8F%AF%E5%A4%AB%E4%B8%8D%E7%AD%89%E5%BC%8F/7565874?fr=aladdin
-
https://www.zhihu.com/question/27821324
-
https://blog.csdn.net/ukakasu/article/details/82688413






















 7621
7621











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








