如何用行列式求解椭圆的面积
同学们大家好,今天我们来学习如何用行列式计算椭圆的面积。
1 中学的思路
在中学的时候,我们是这样推导的。设椭圆的焦点在 轴上,半长轴和半短轴为
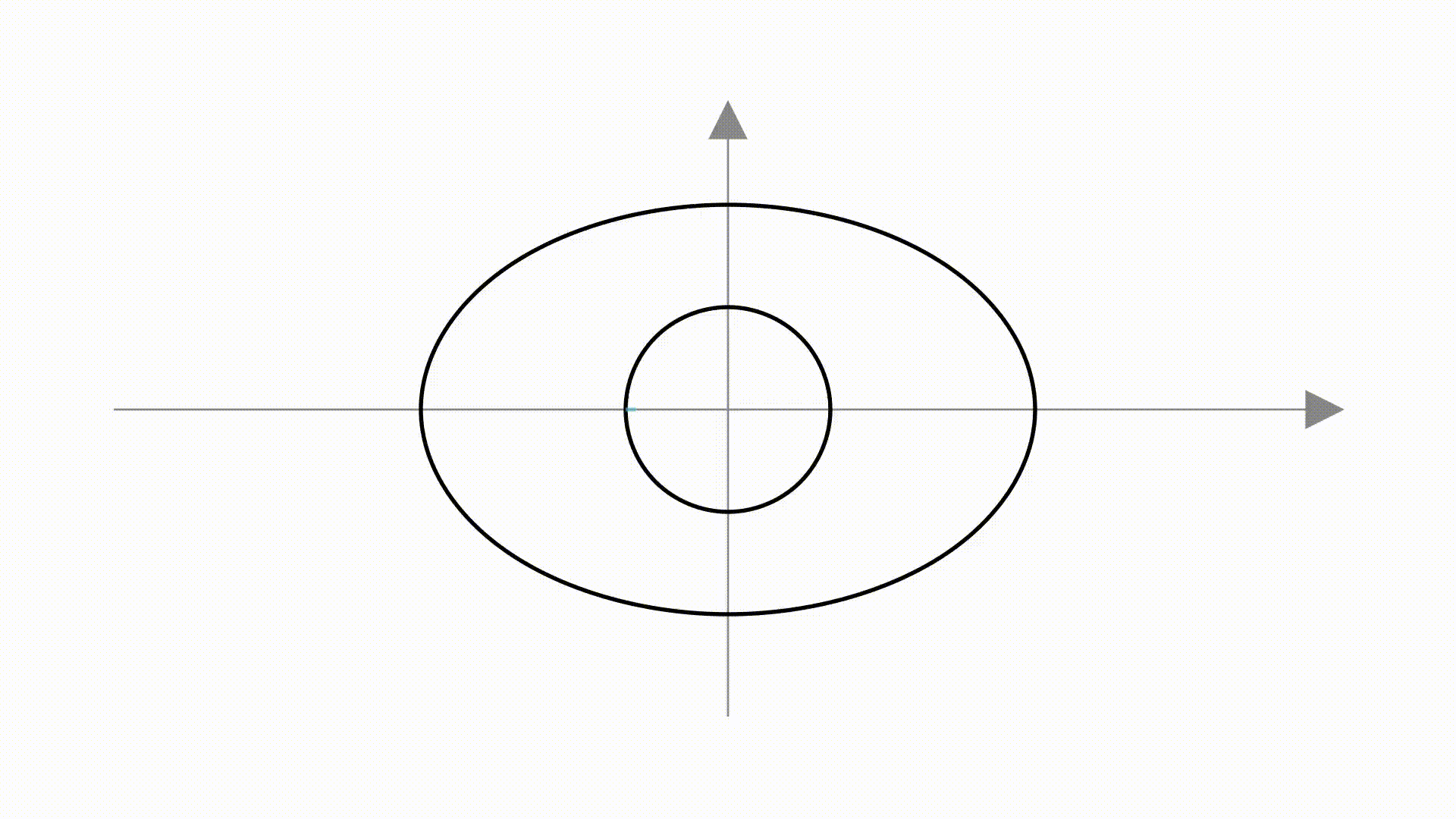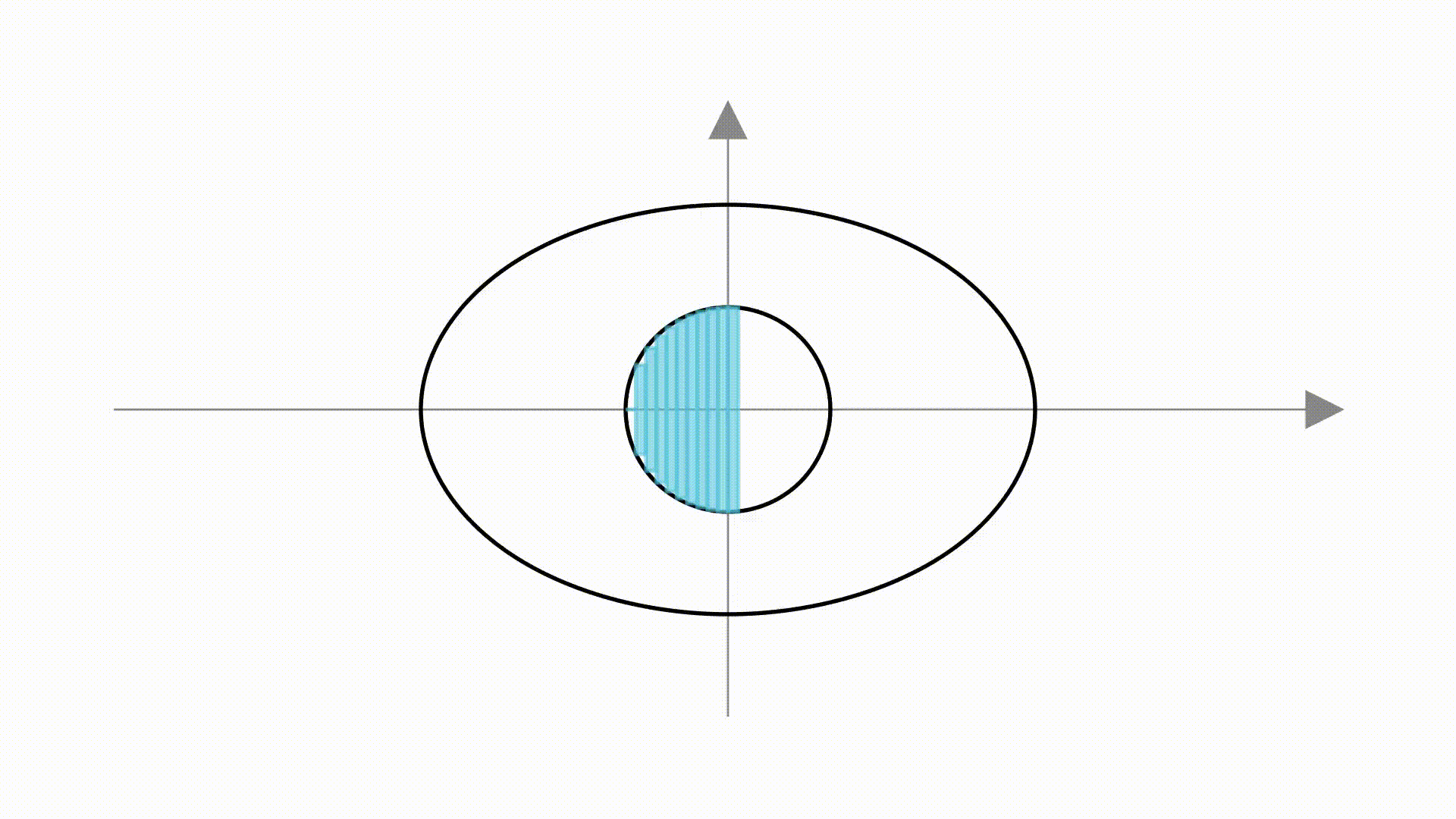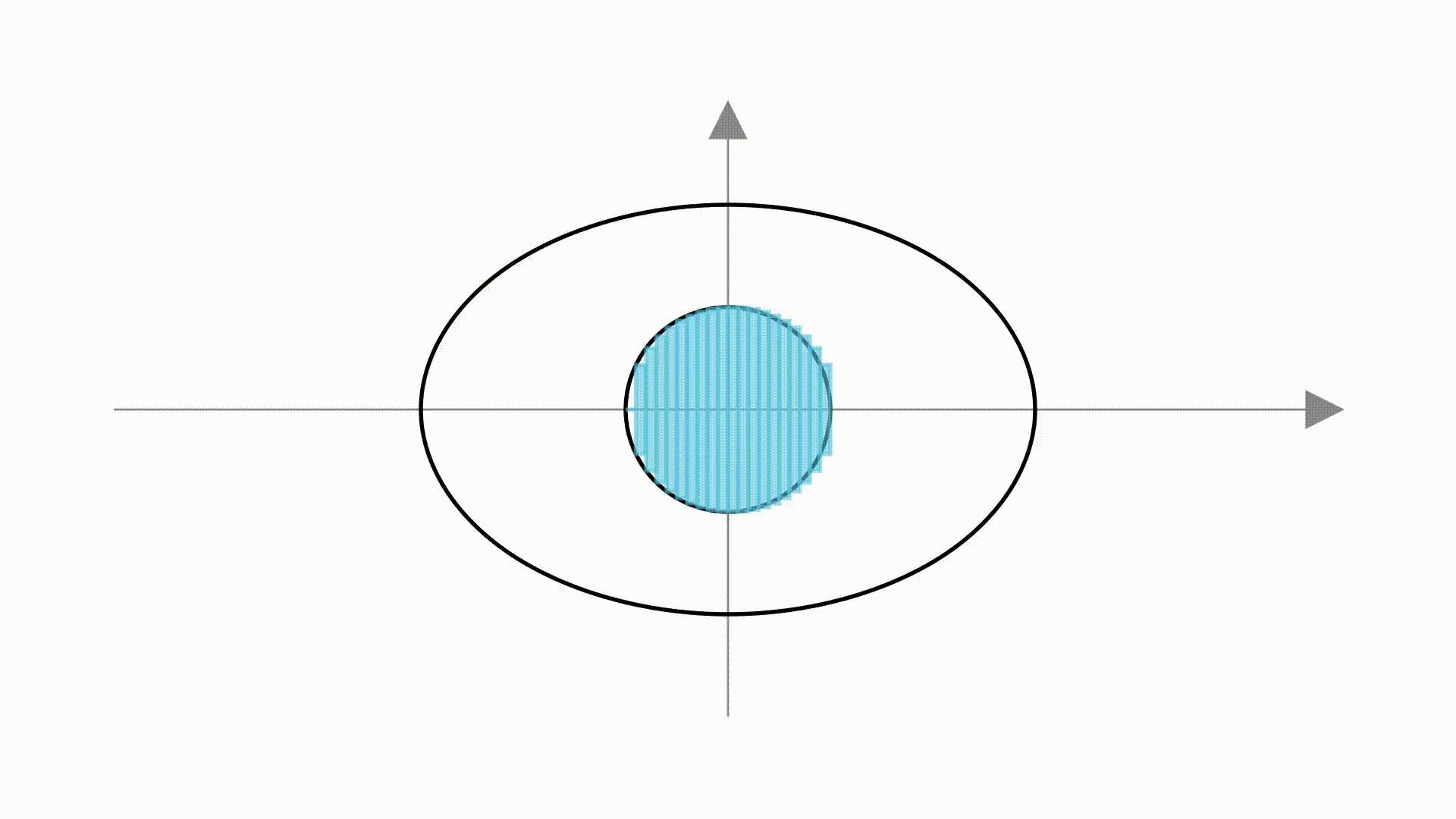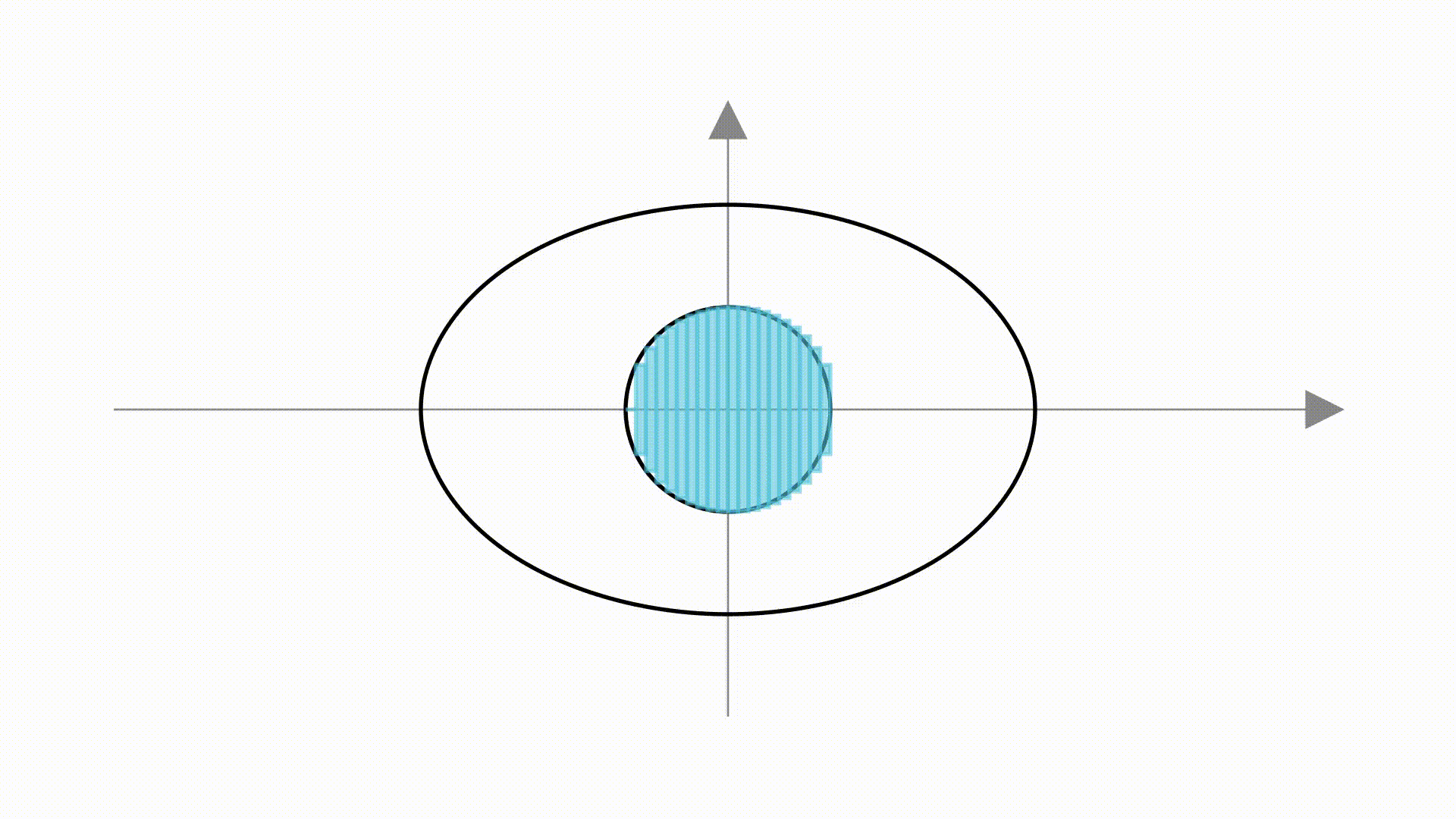
,则它的图像是这样的。

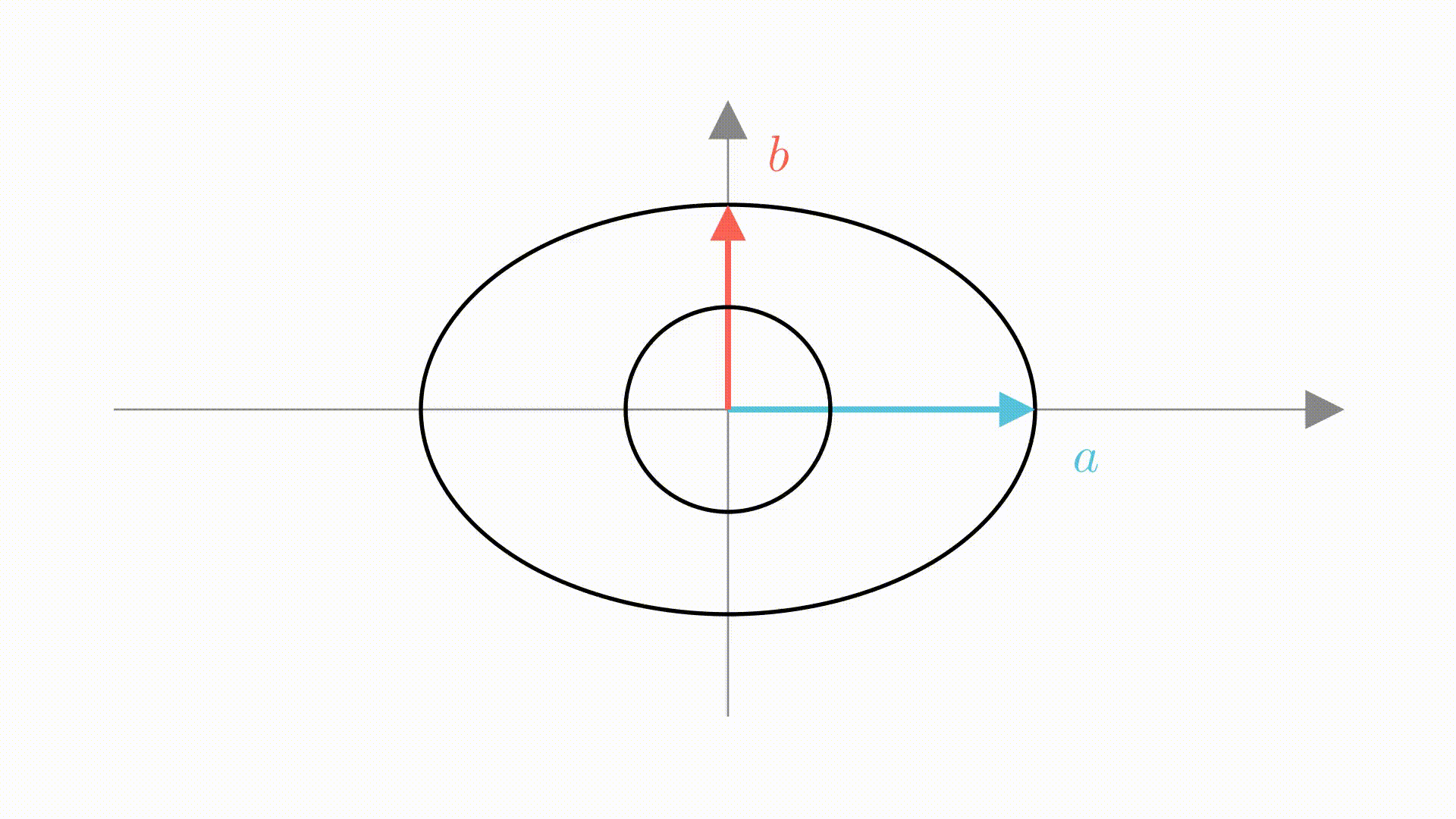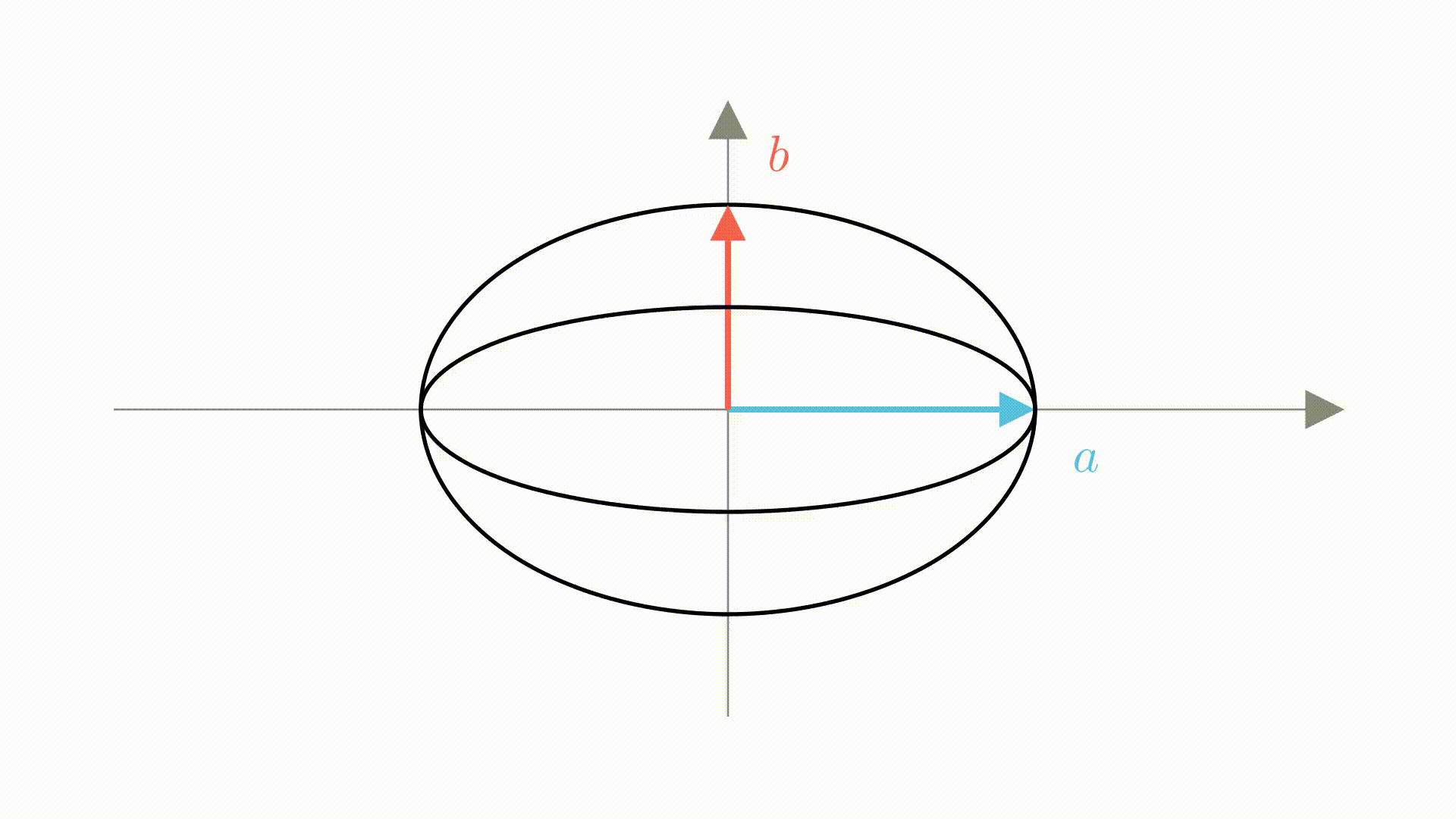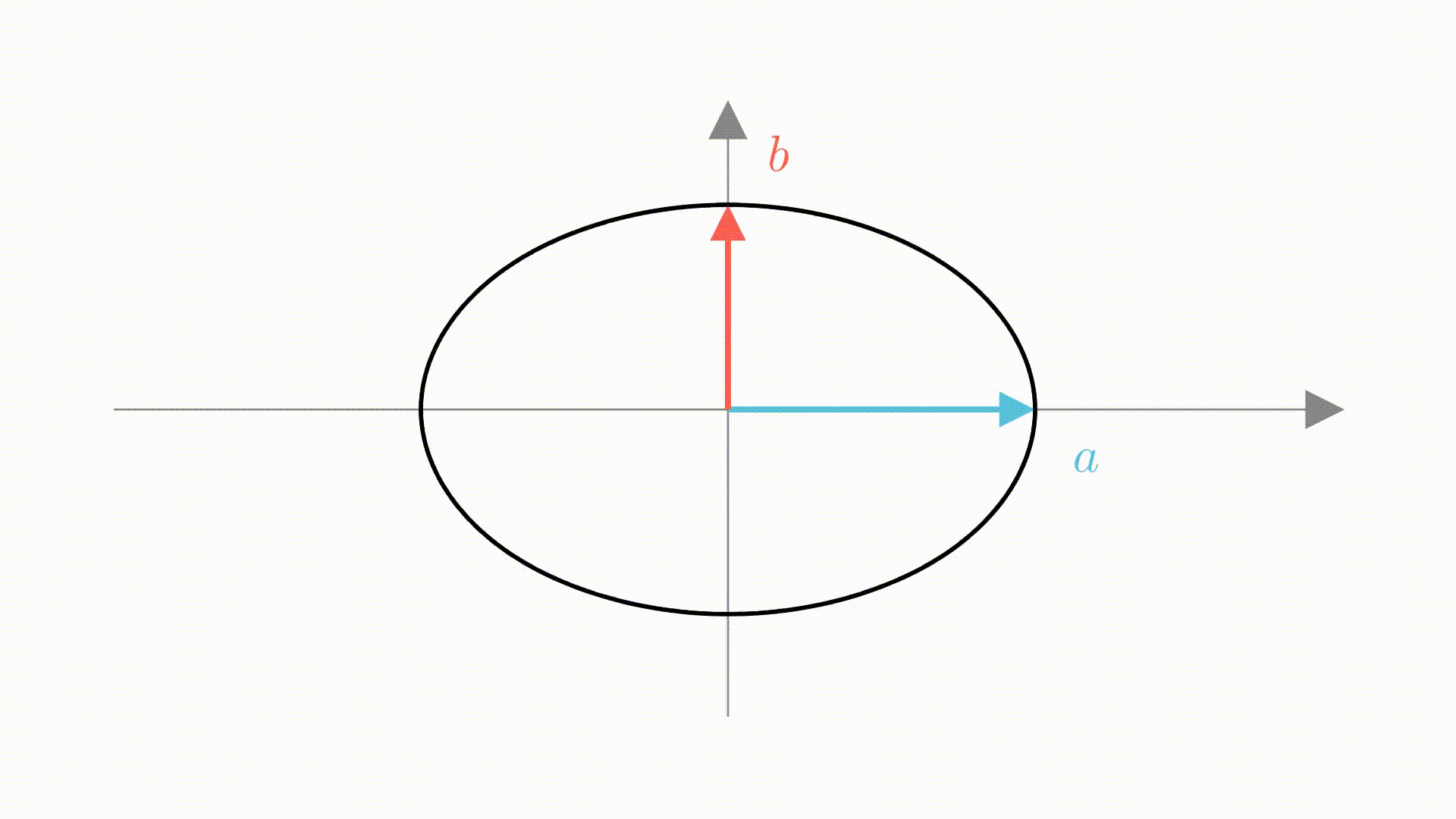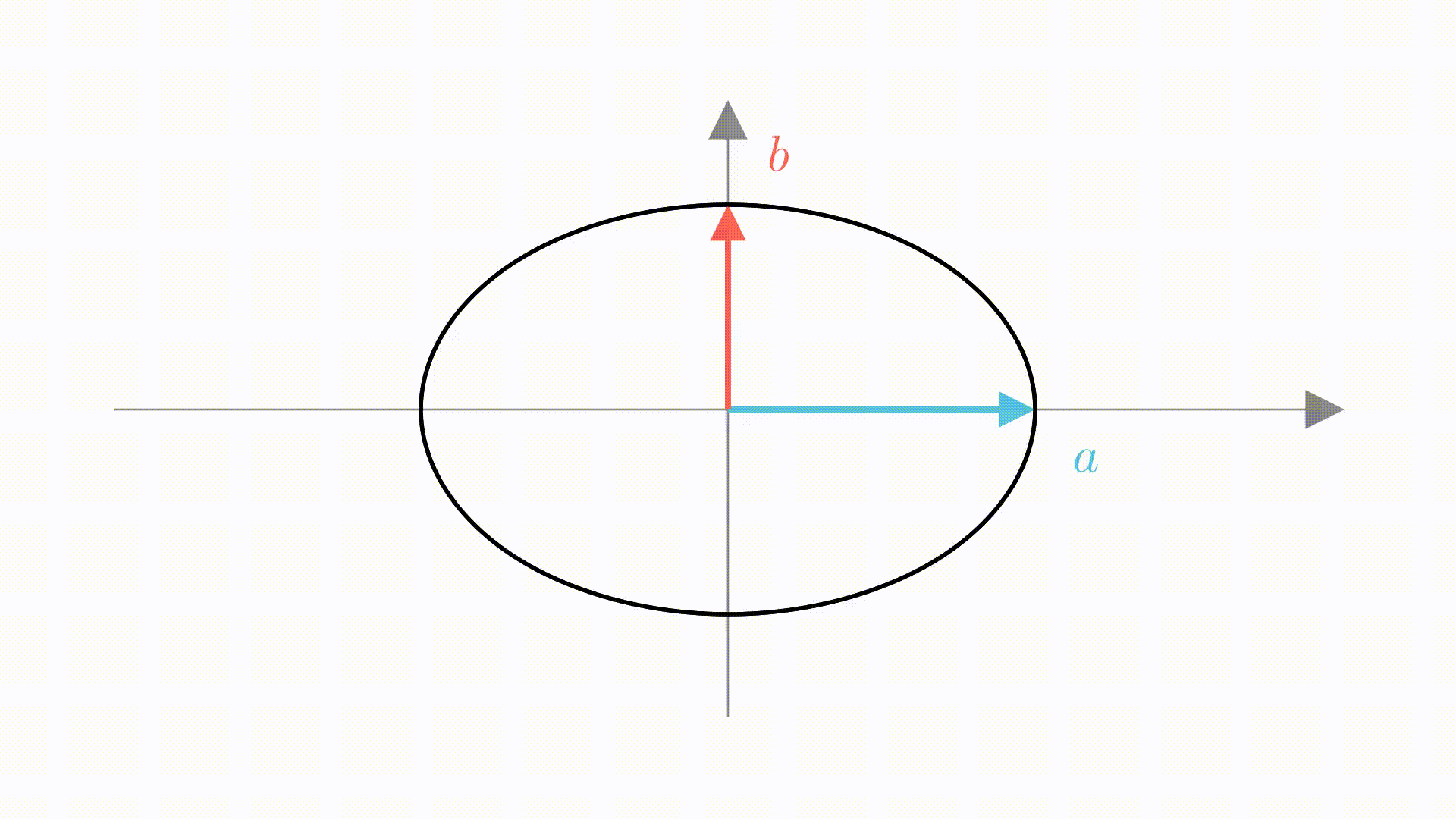
在里面画上一个单位圆

直观上,我们可以看出,它是单位圆在 轴上增长
倍,
轴上增长
倍形成的
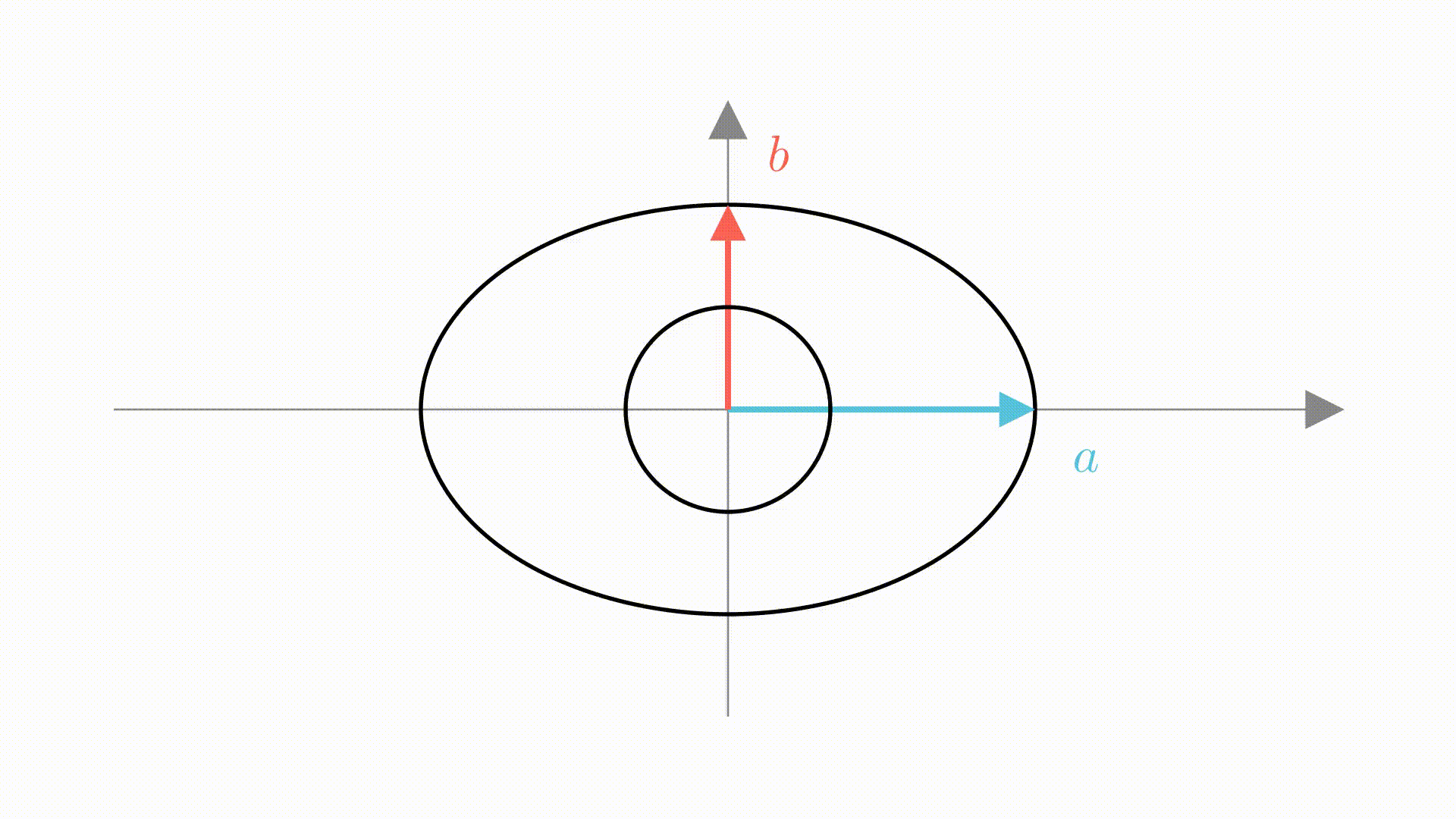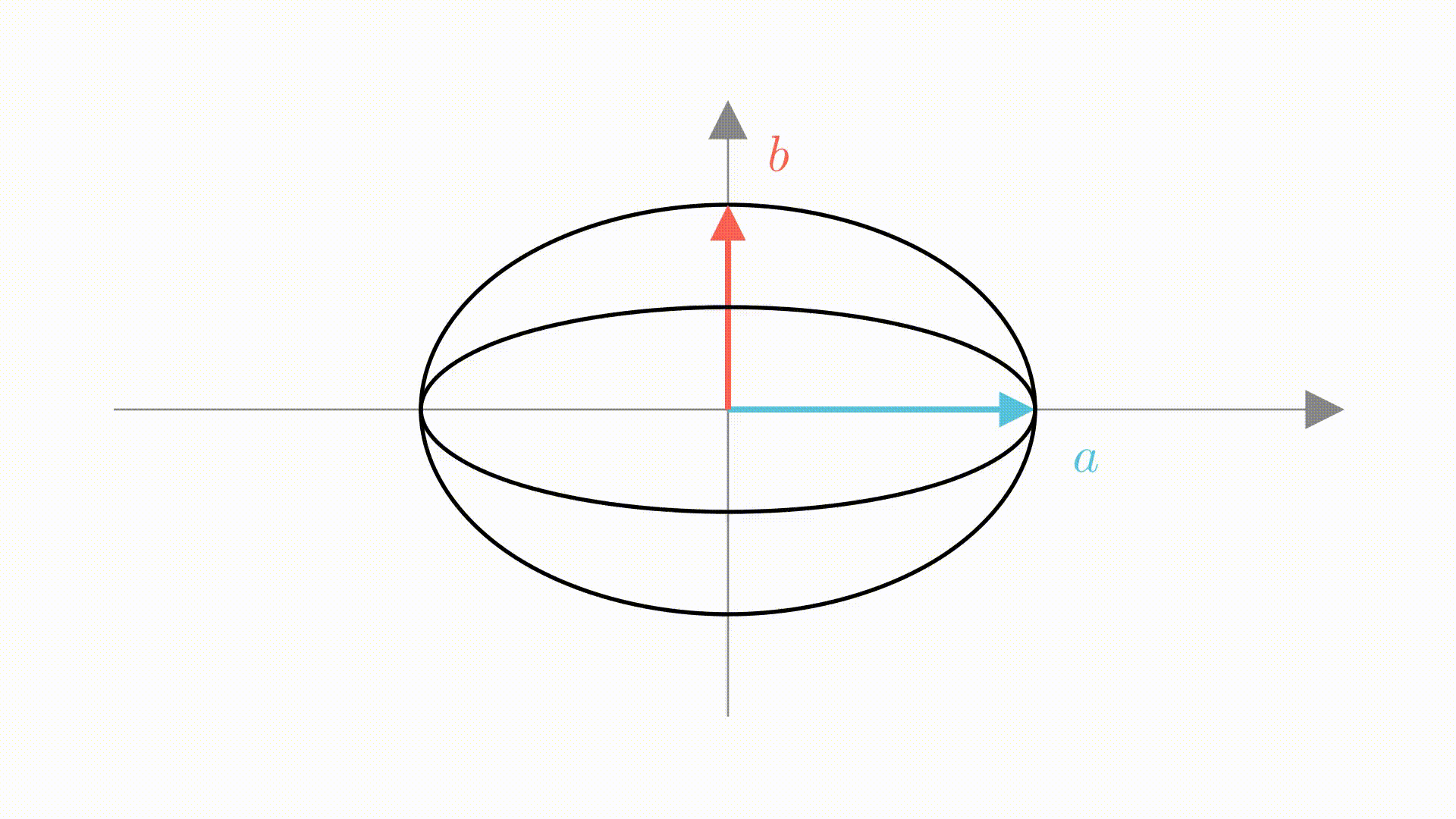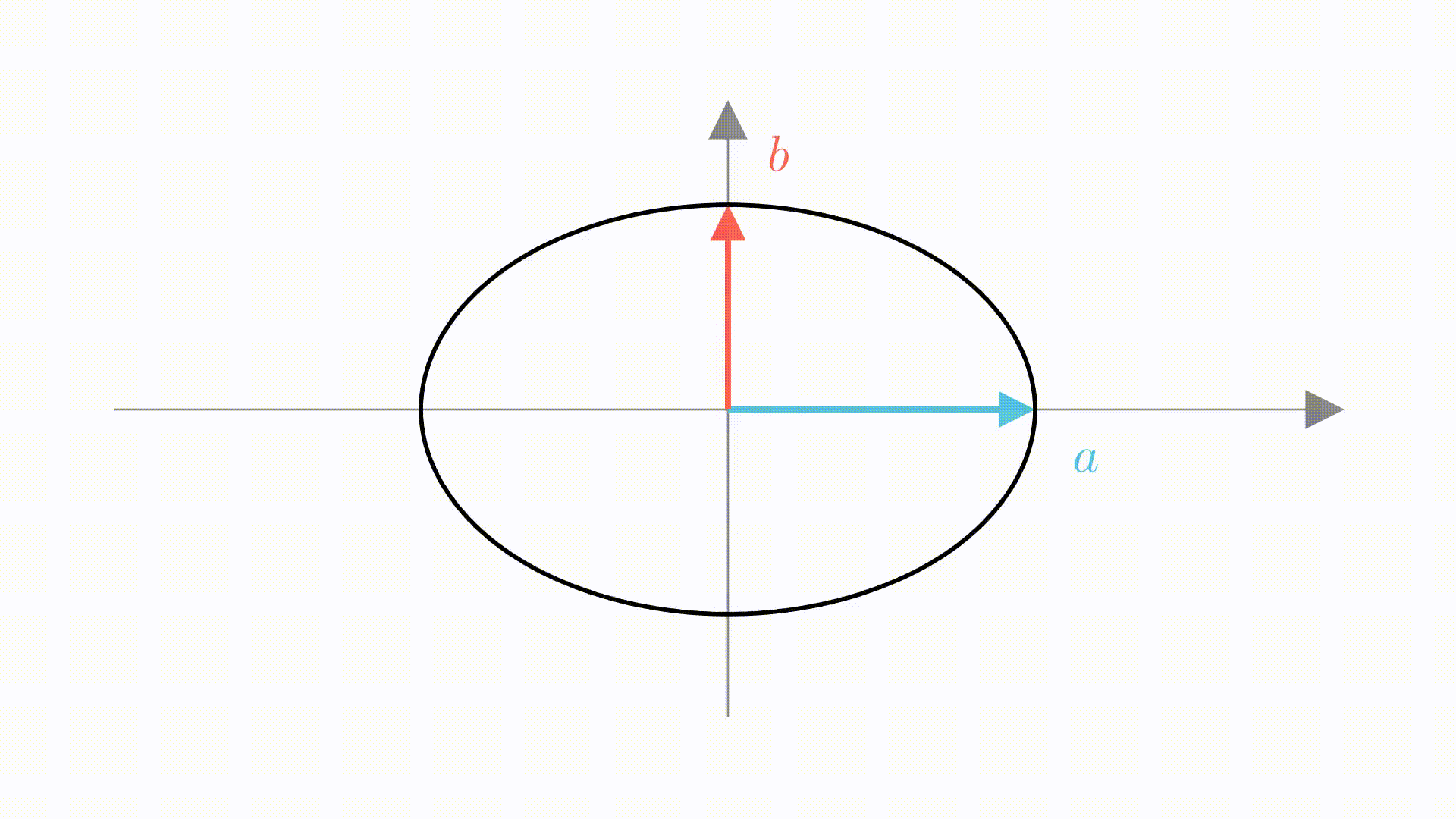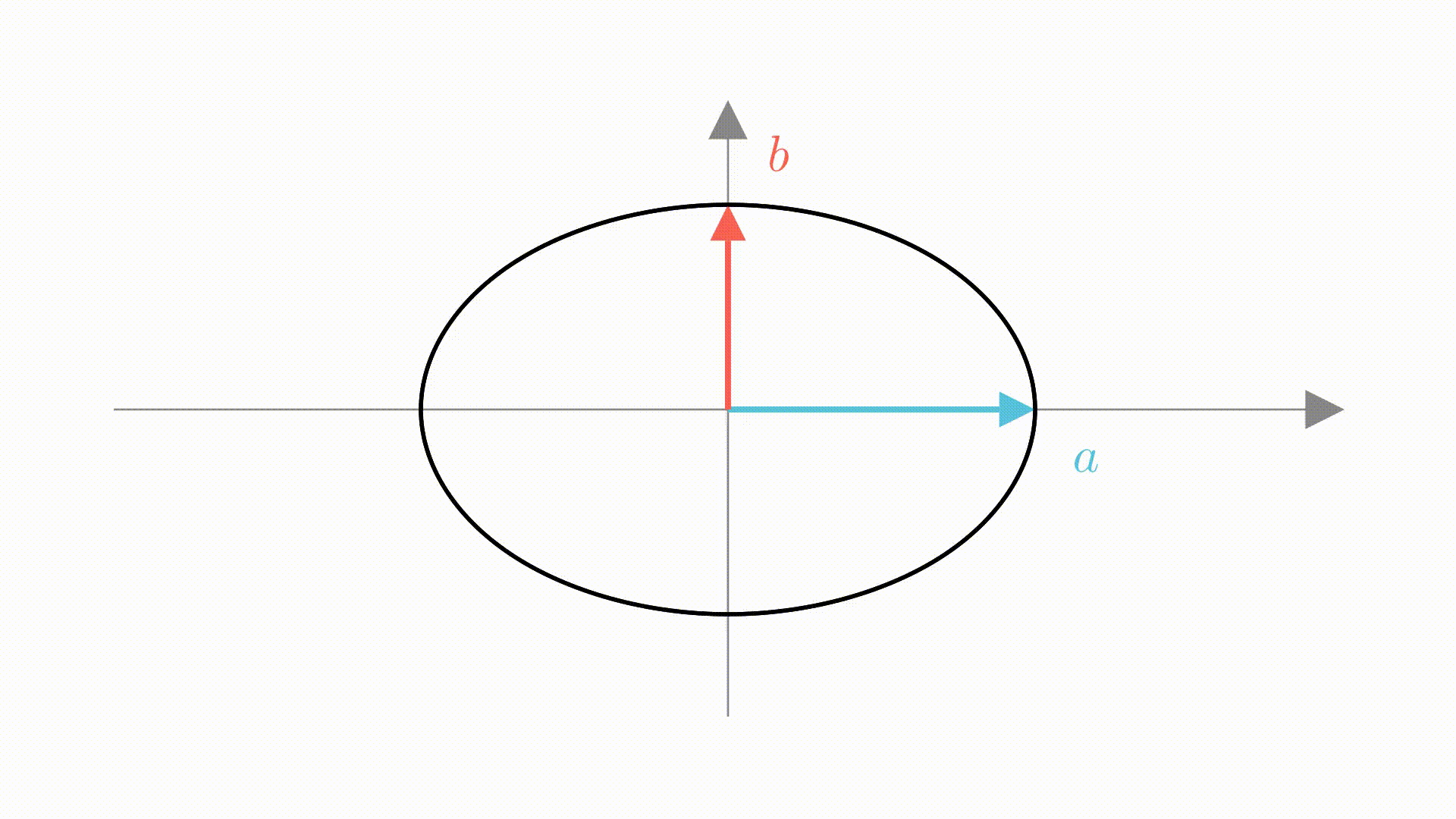
如果,把单位圆看成是若干个矩形组成的。
那么,在圆变成椭圆的过程中,就是把矩形的两条边增大了 倍和
倍。
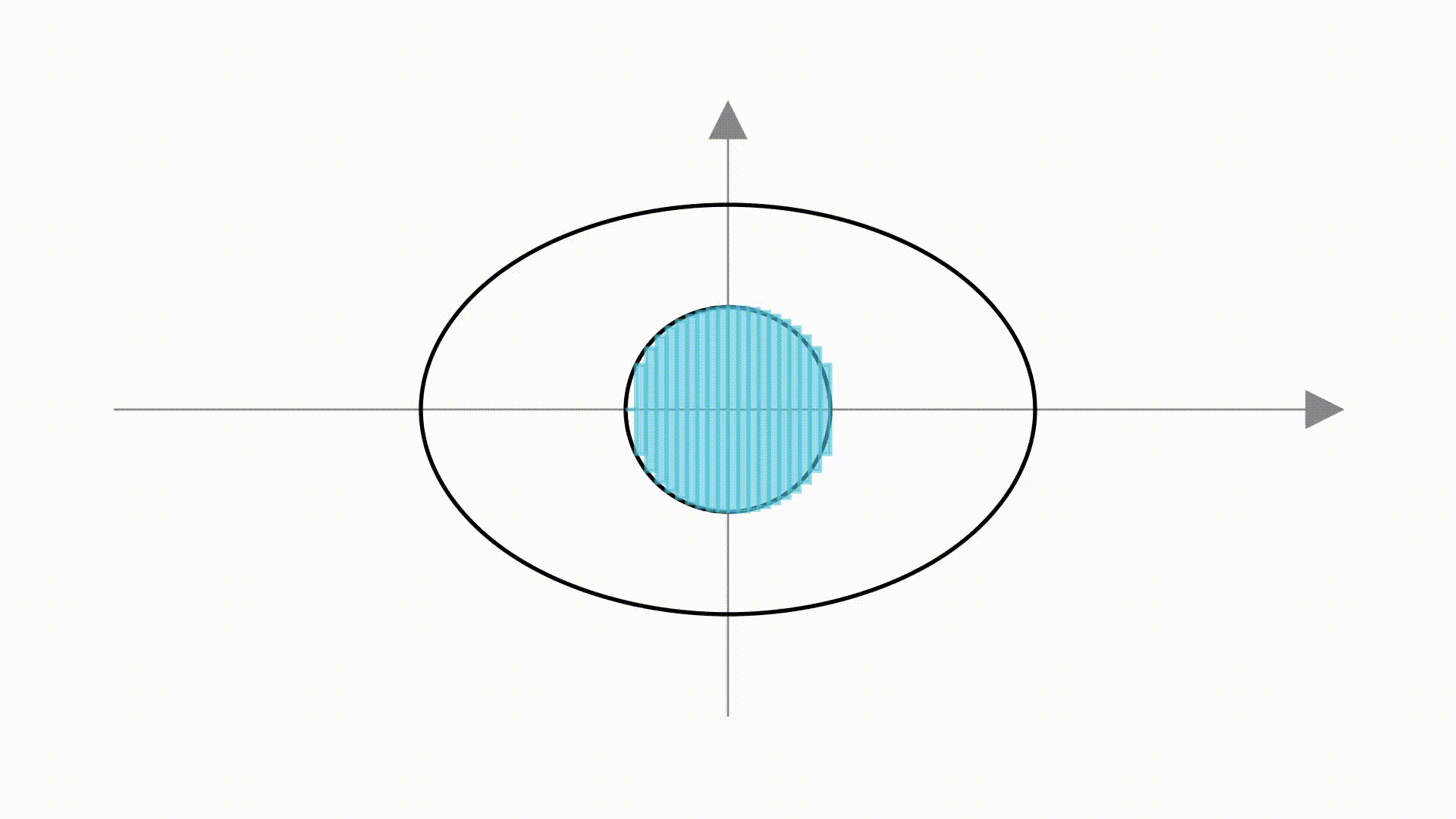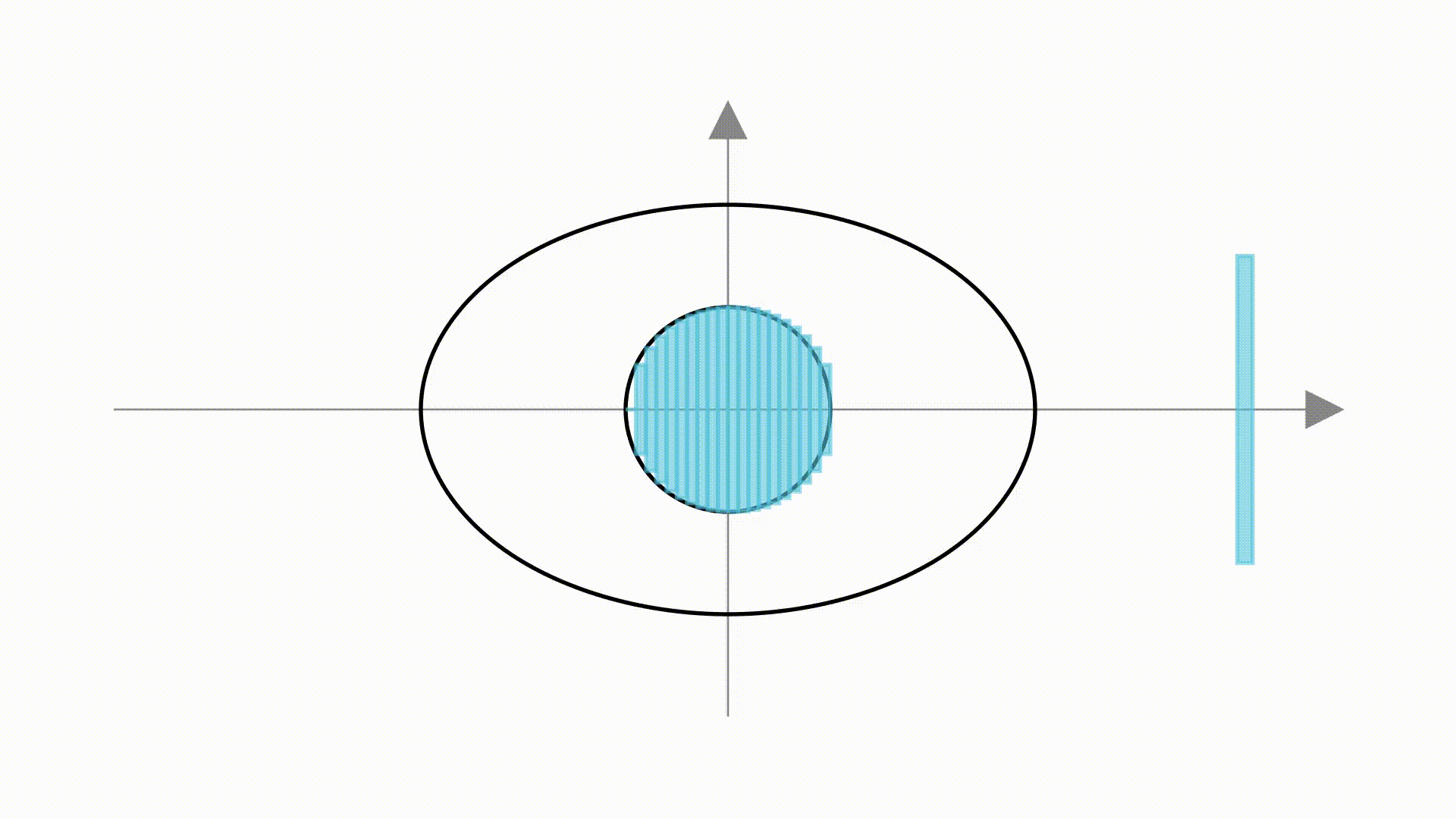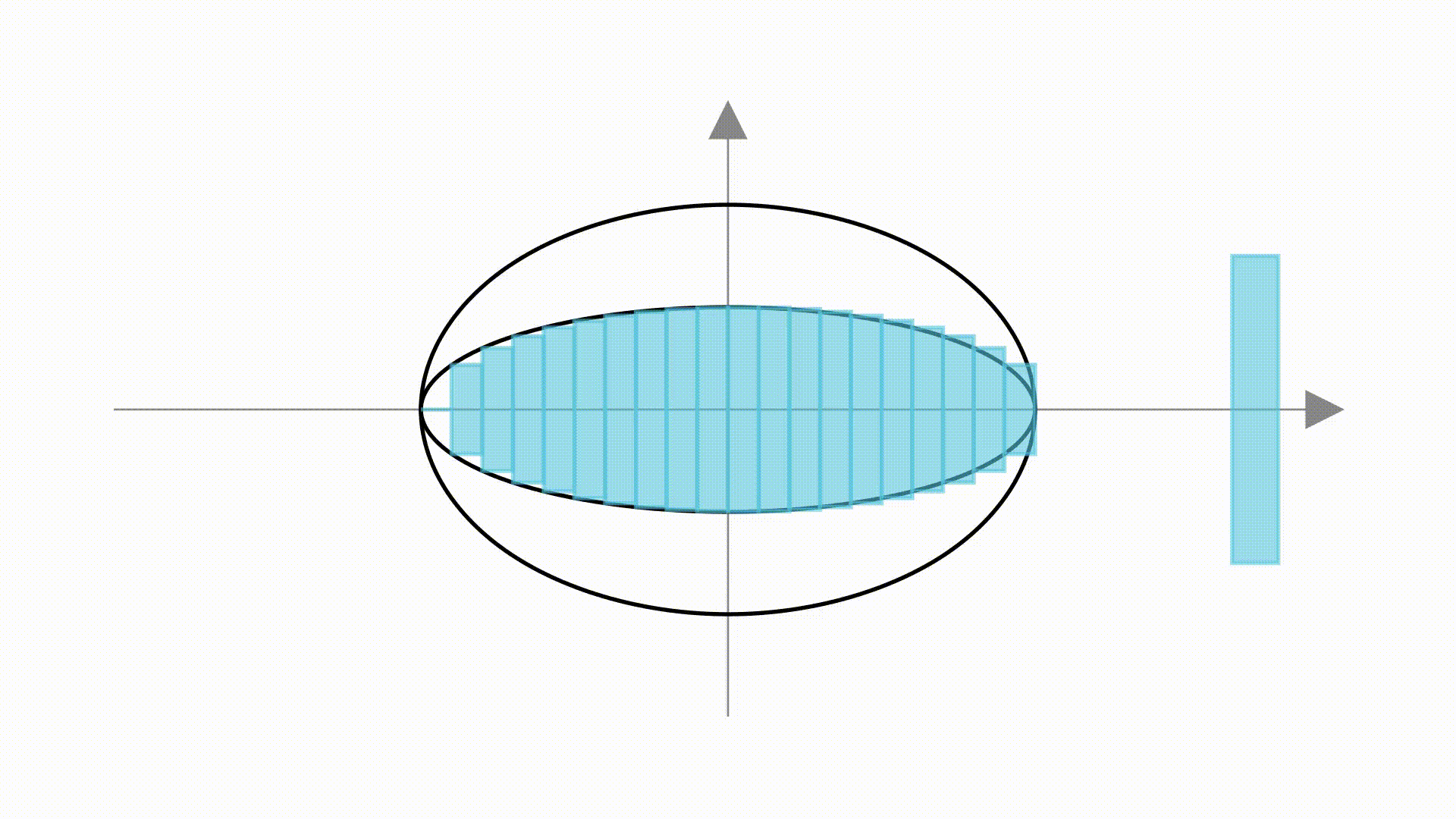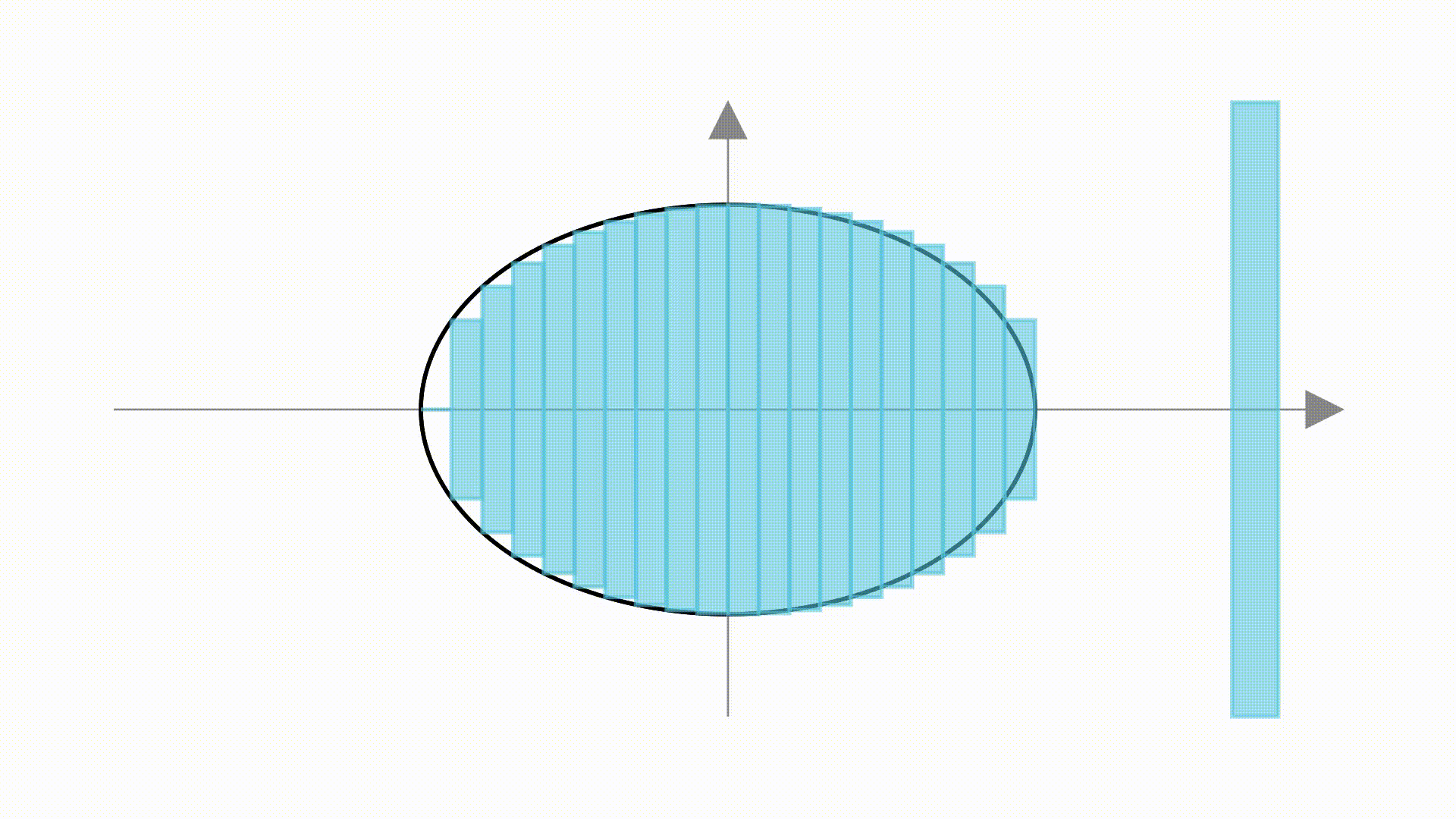
这样椭圆的面积就是单位圆的 倍,从而得出椭圆面积为

这个方法虽然很直观,但缺乏严谨性。比如肉眼可见的,左边部分的矩形并没填满圆,右边部分的矩形又超过了圆。

2 思想
下面,我们借用线代的工具来完成椭圆面积的推导,思路还是刚刚那个思路。将单位圆在 轴上增长
倍,
轴上增长
倍形成椭圆。
只是把这段过程,用矩阵来描述
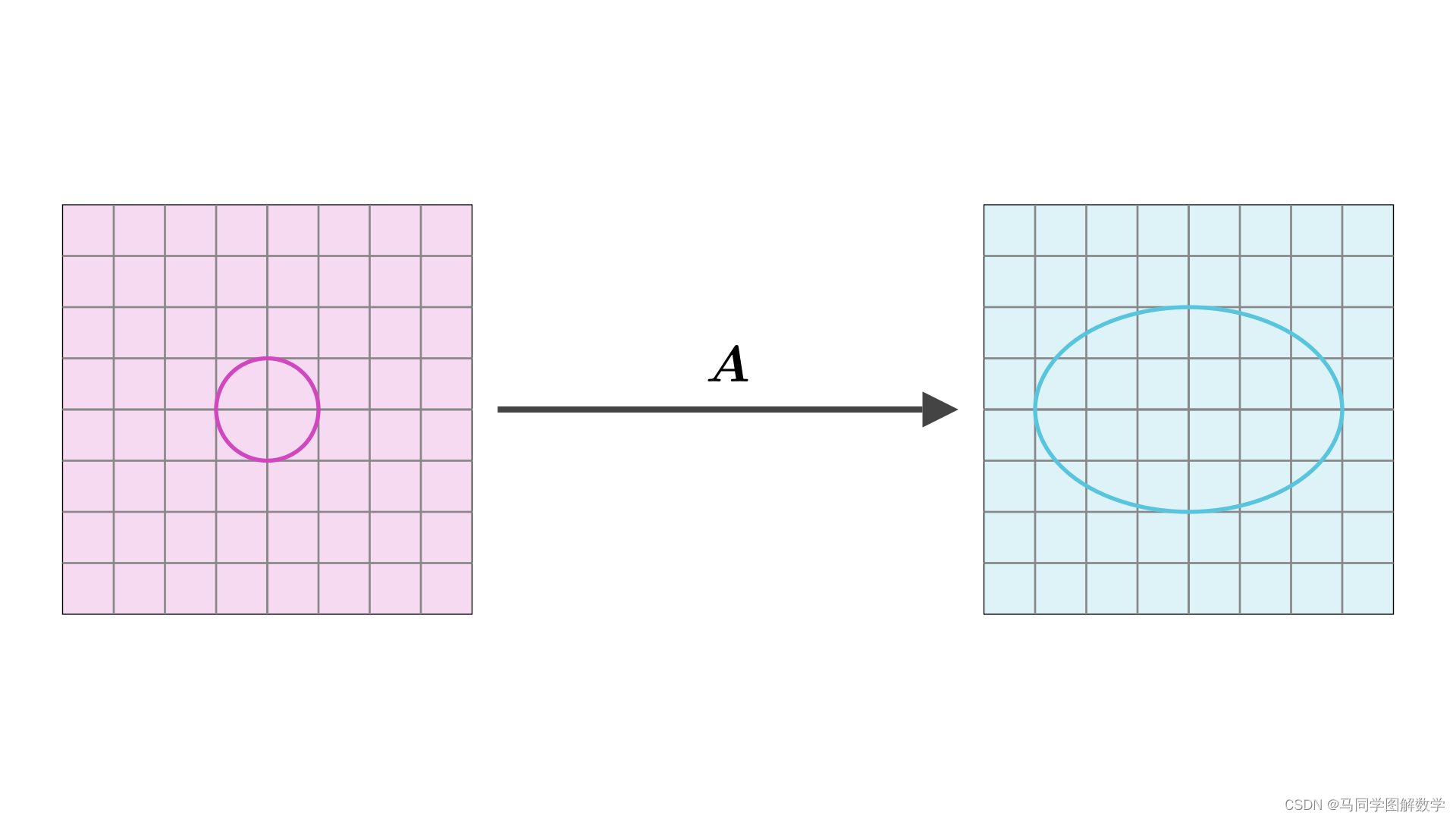
假如我们可以将圆与椭圆用向量来表示,并且求解出变换矩阵 。那么根据行列式的几何意义可以知道,变换后的面积,比上变换前的面积,就等于行列式。这样
![]()
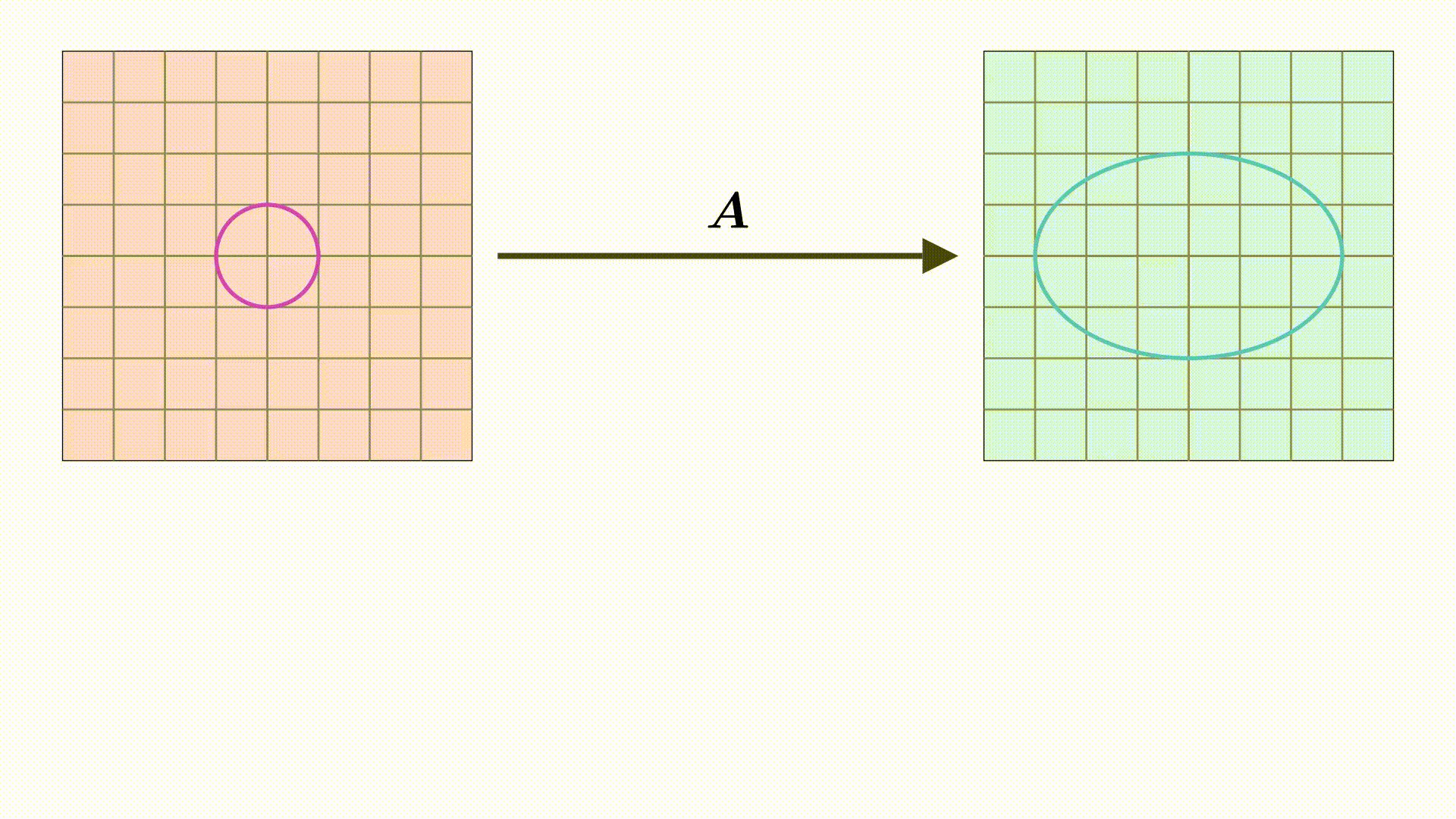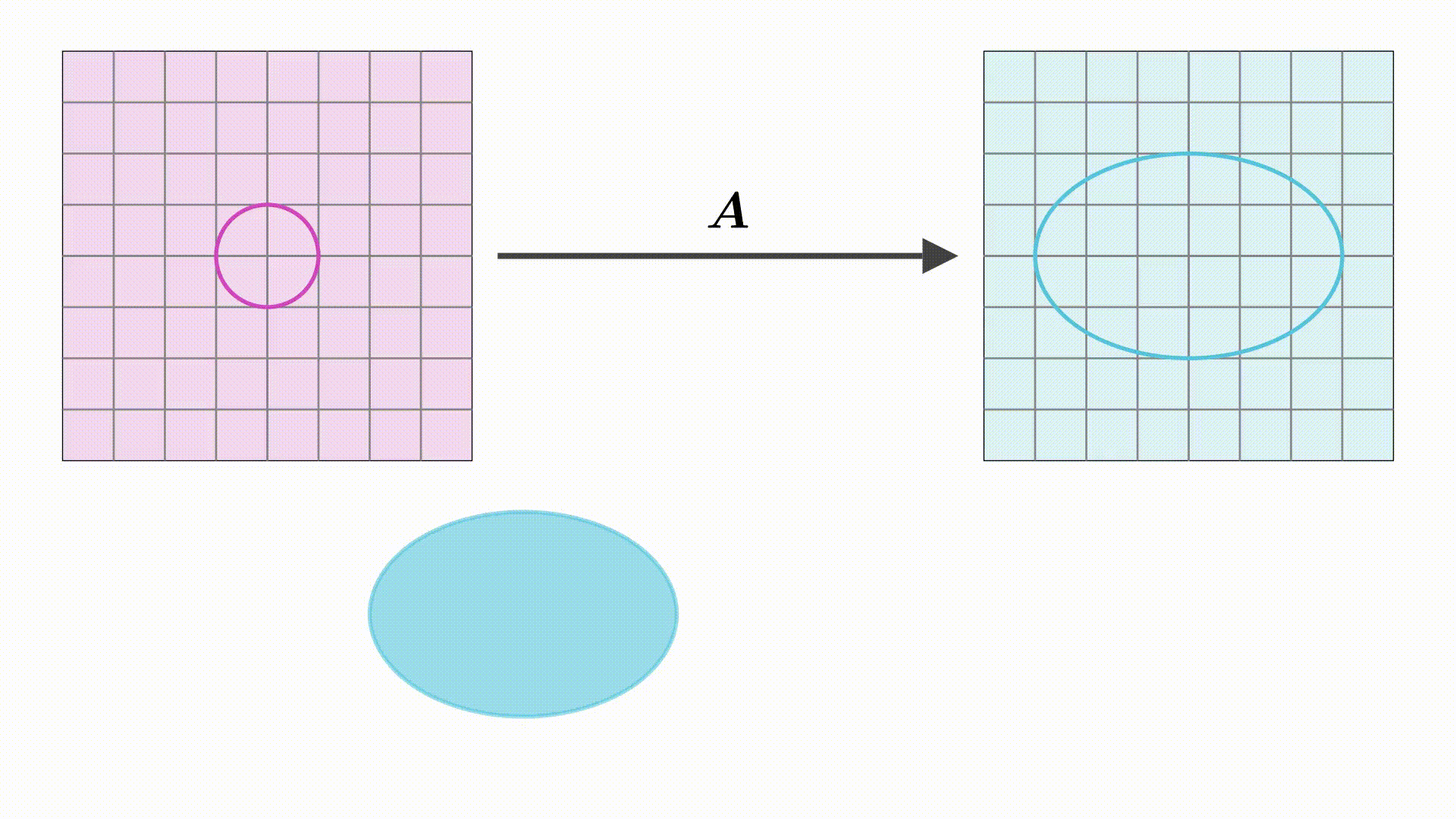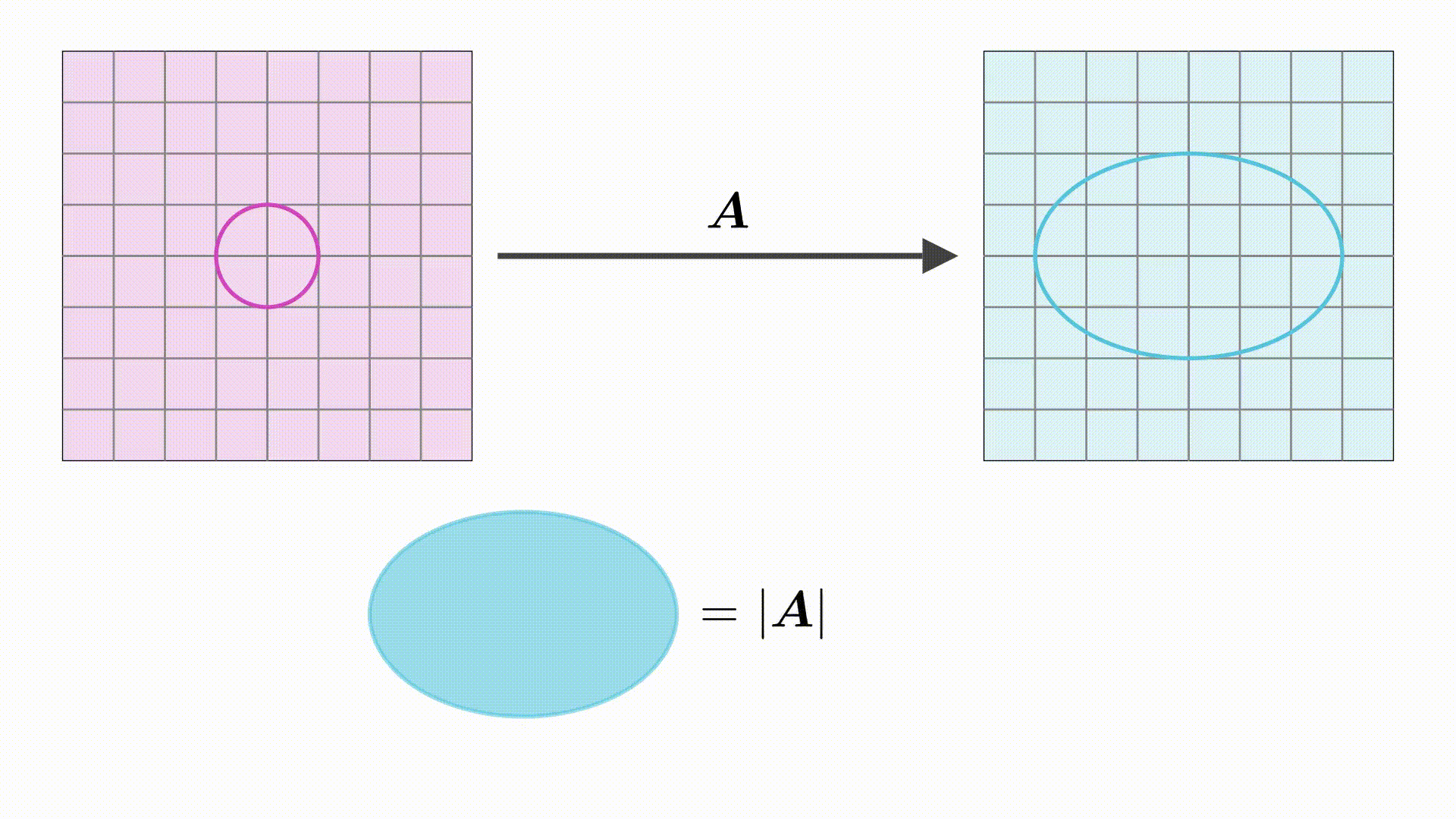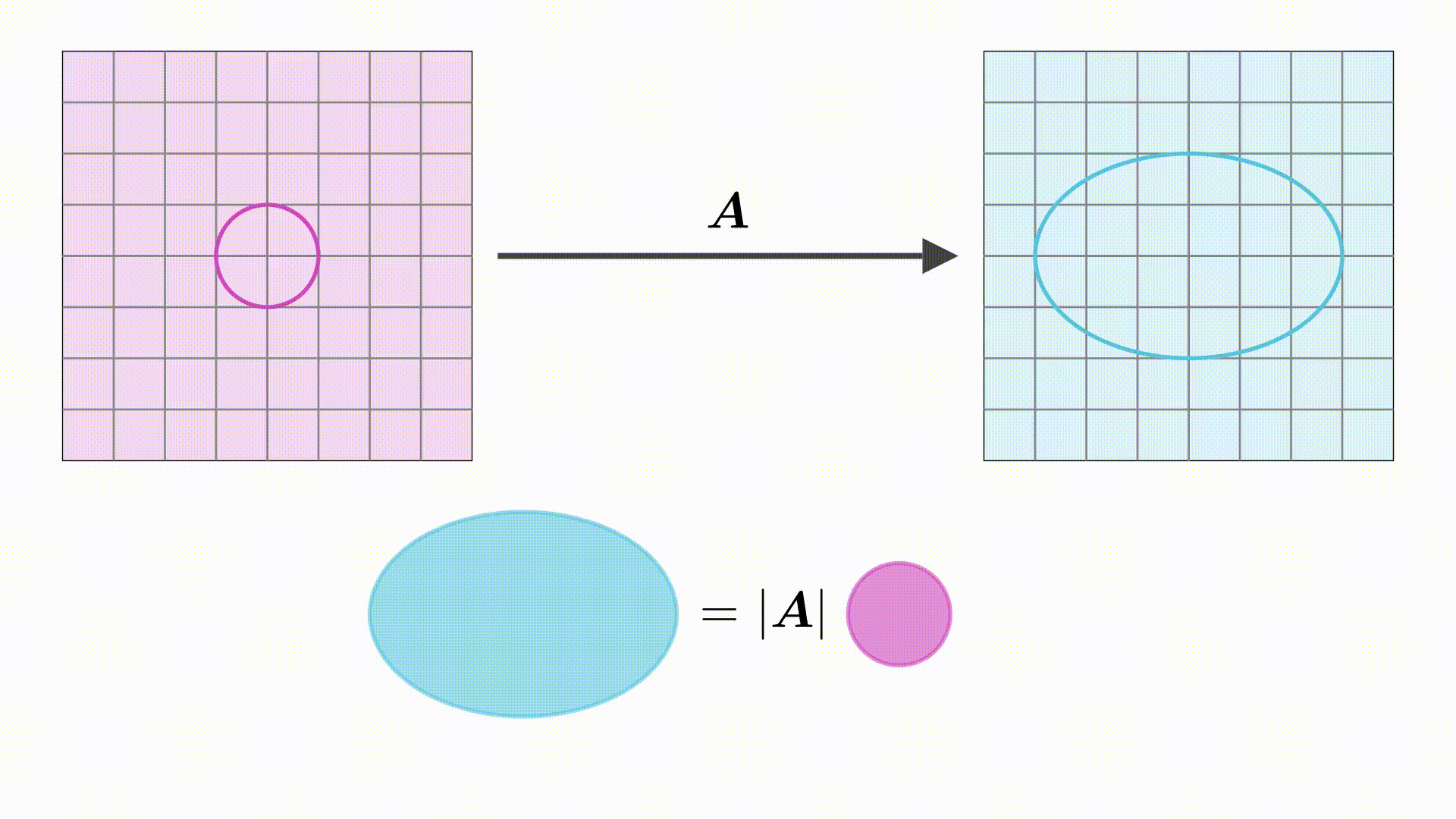
3 圆和椭圆的表示
思路有了,下面开始具体操作。首先写出圆的参数方程,因为单位圆的半径为1,所以其参数方程为
据此,将它改写成一个二维向量
这个向量存在在二维平面中,当 取具体值时,它就是平面上的一个点,当
在
到
范围内变化时,它就是圆
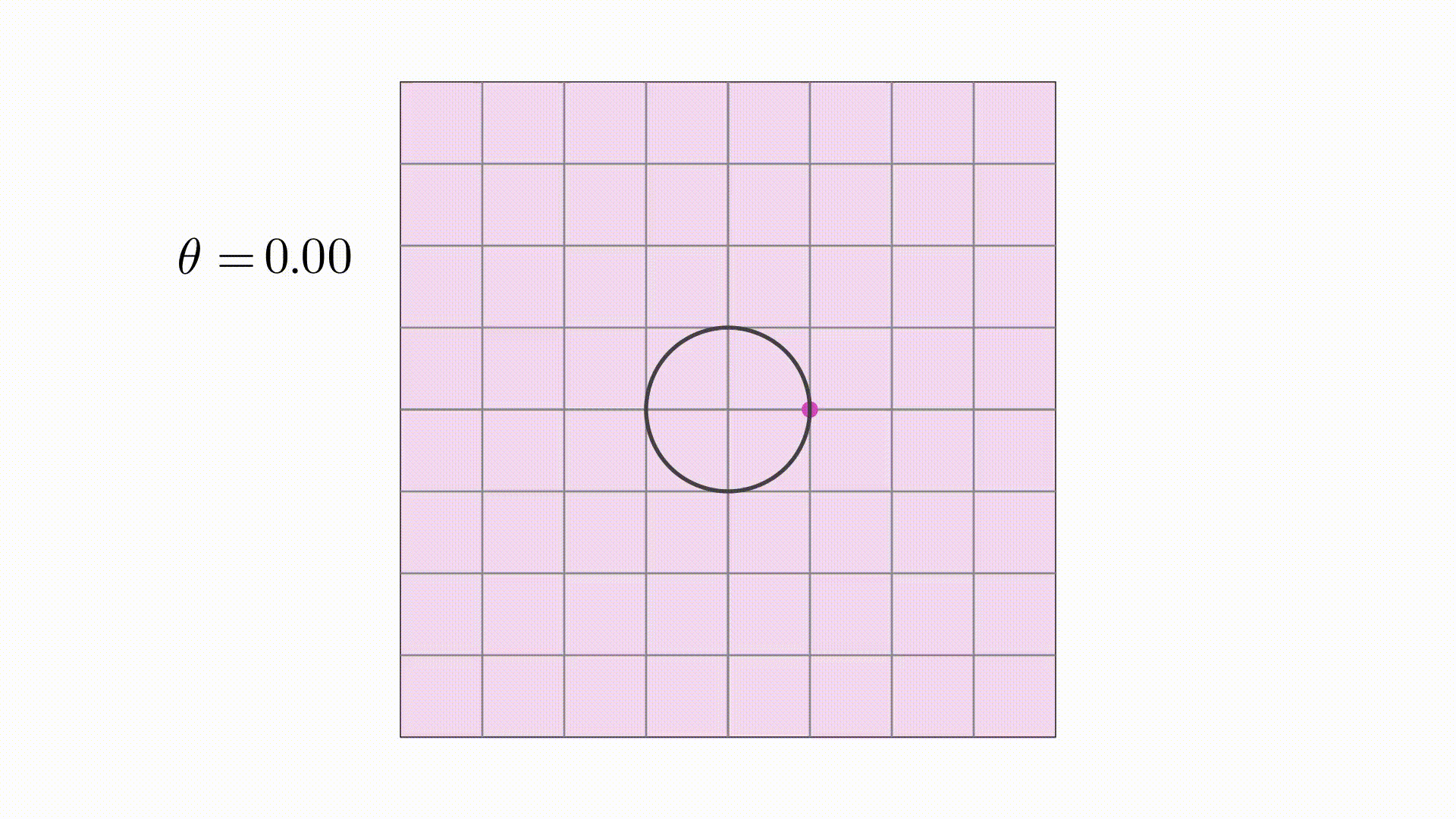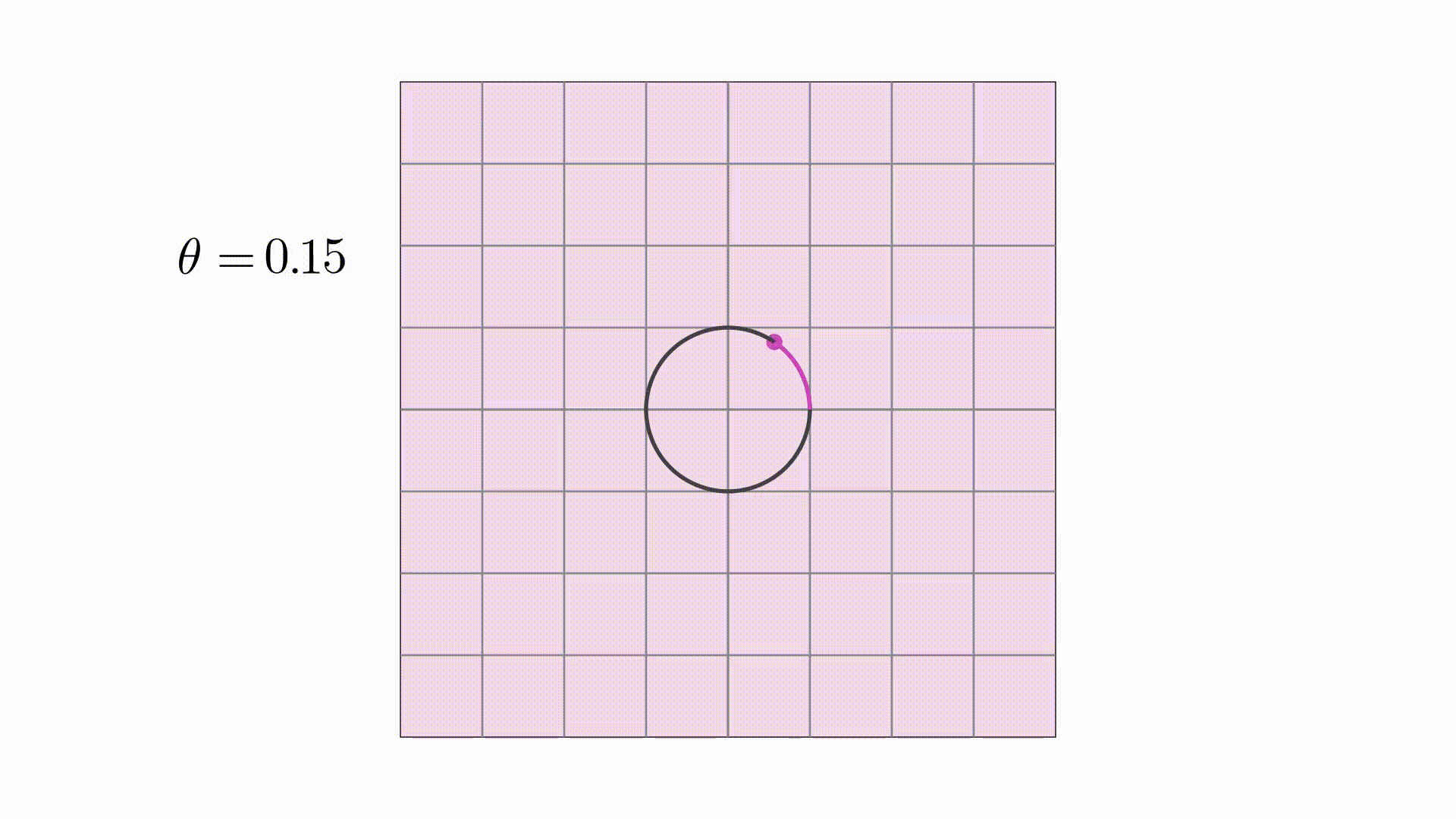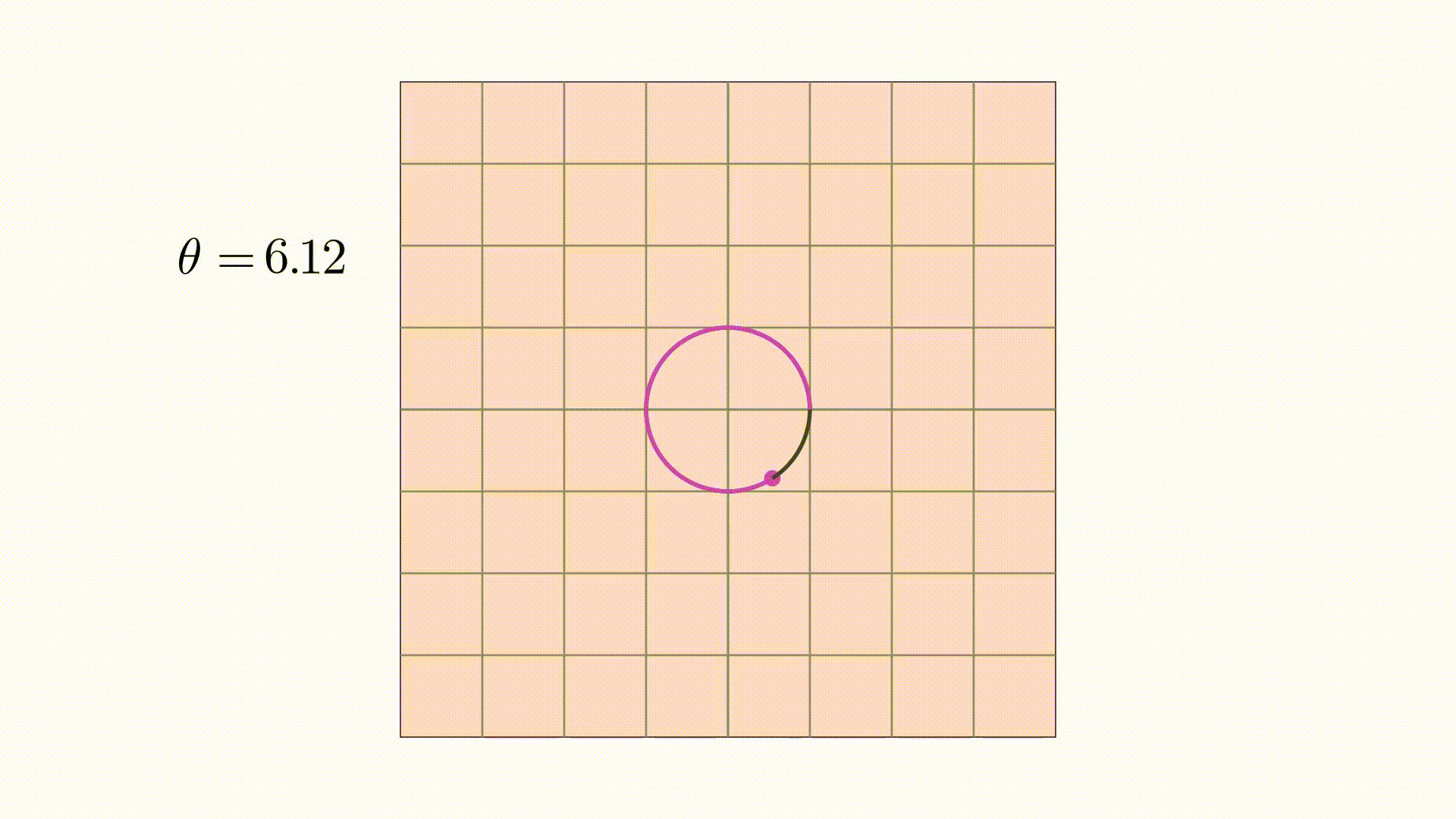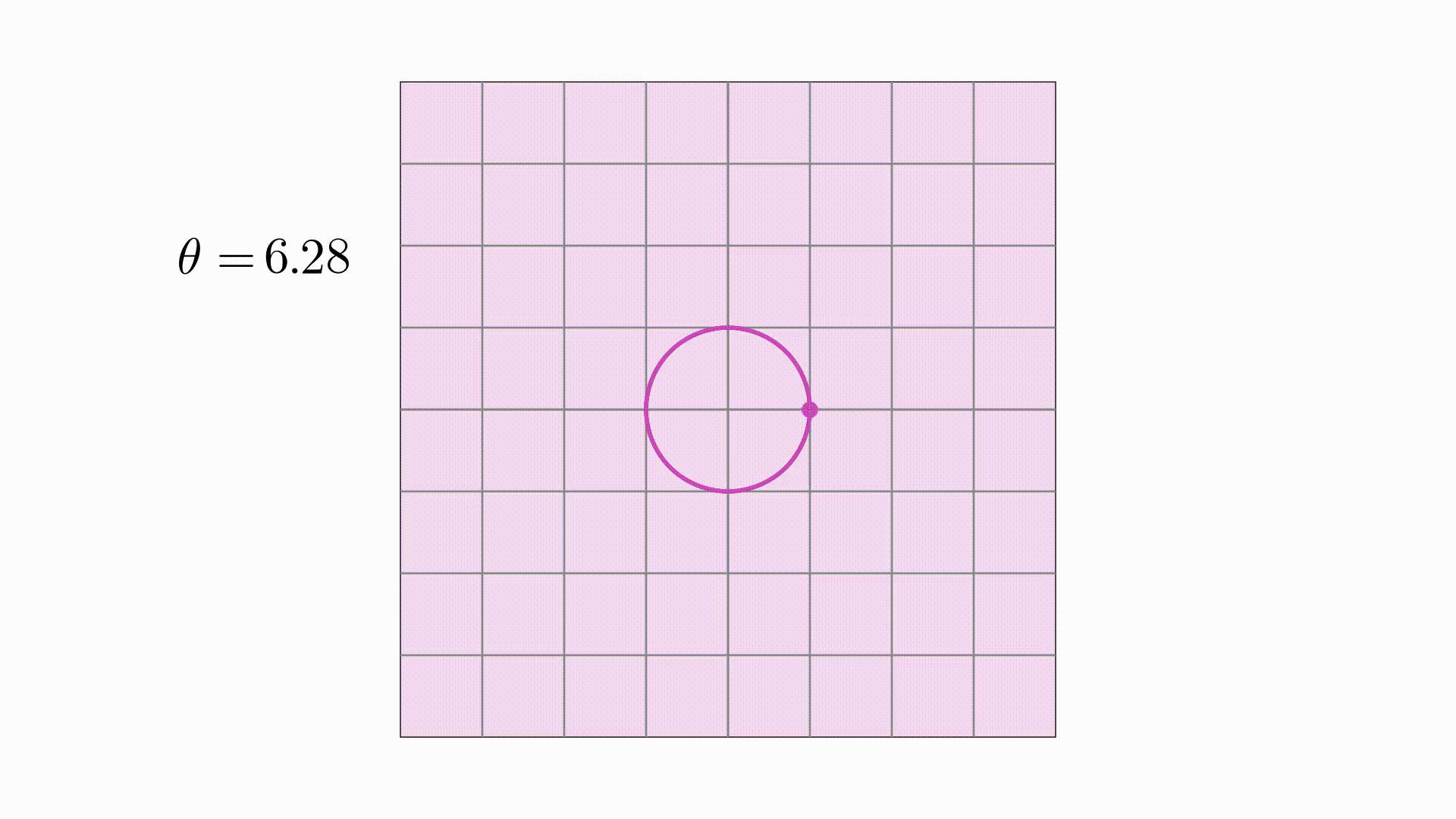
同样的,根据椭圆的参数方程,可以写出其向量形式
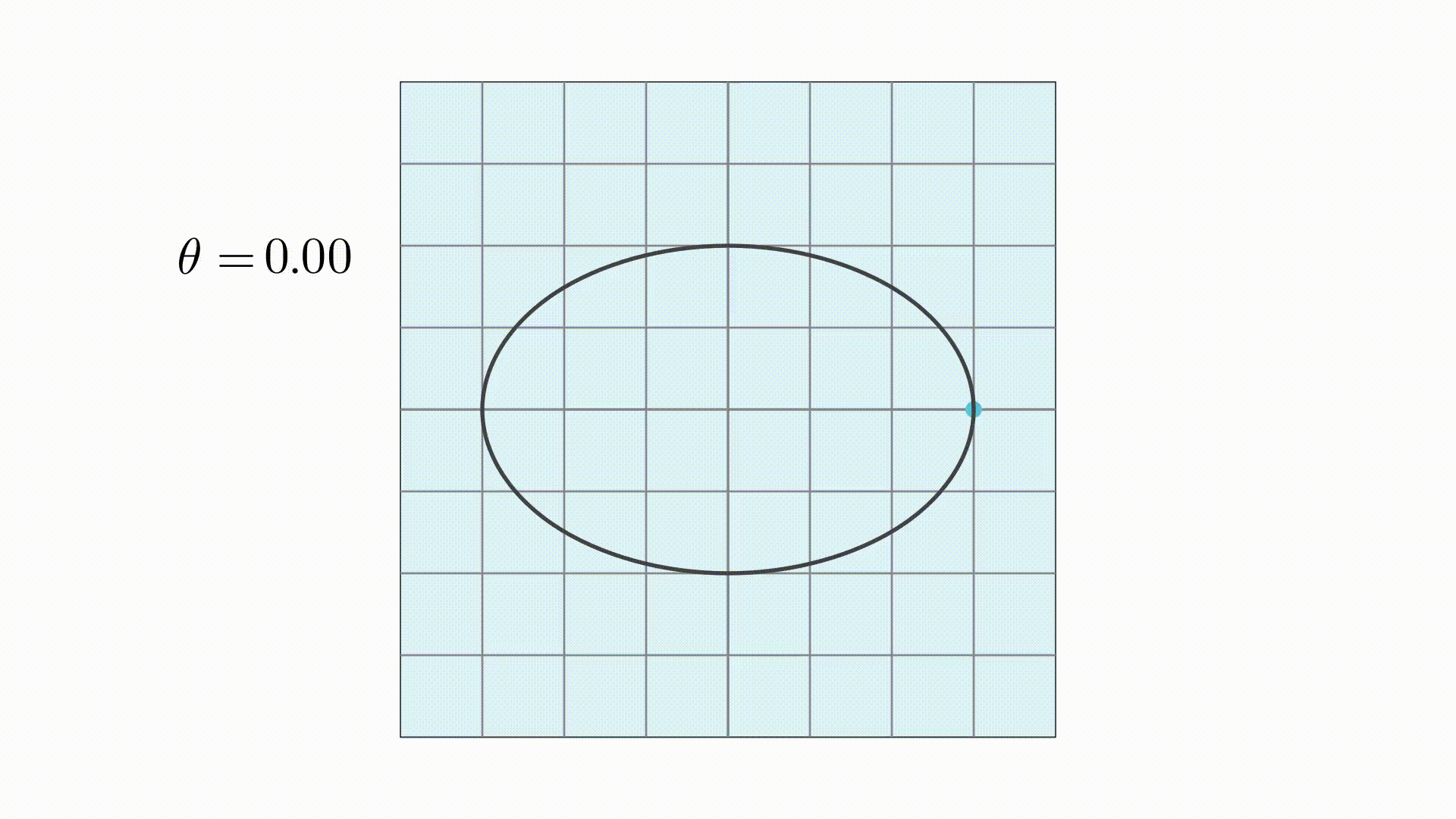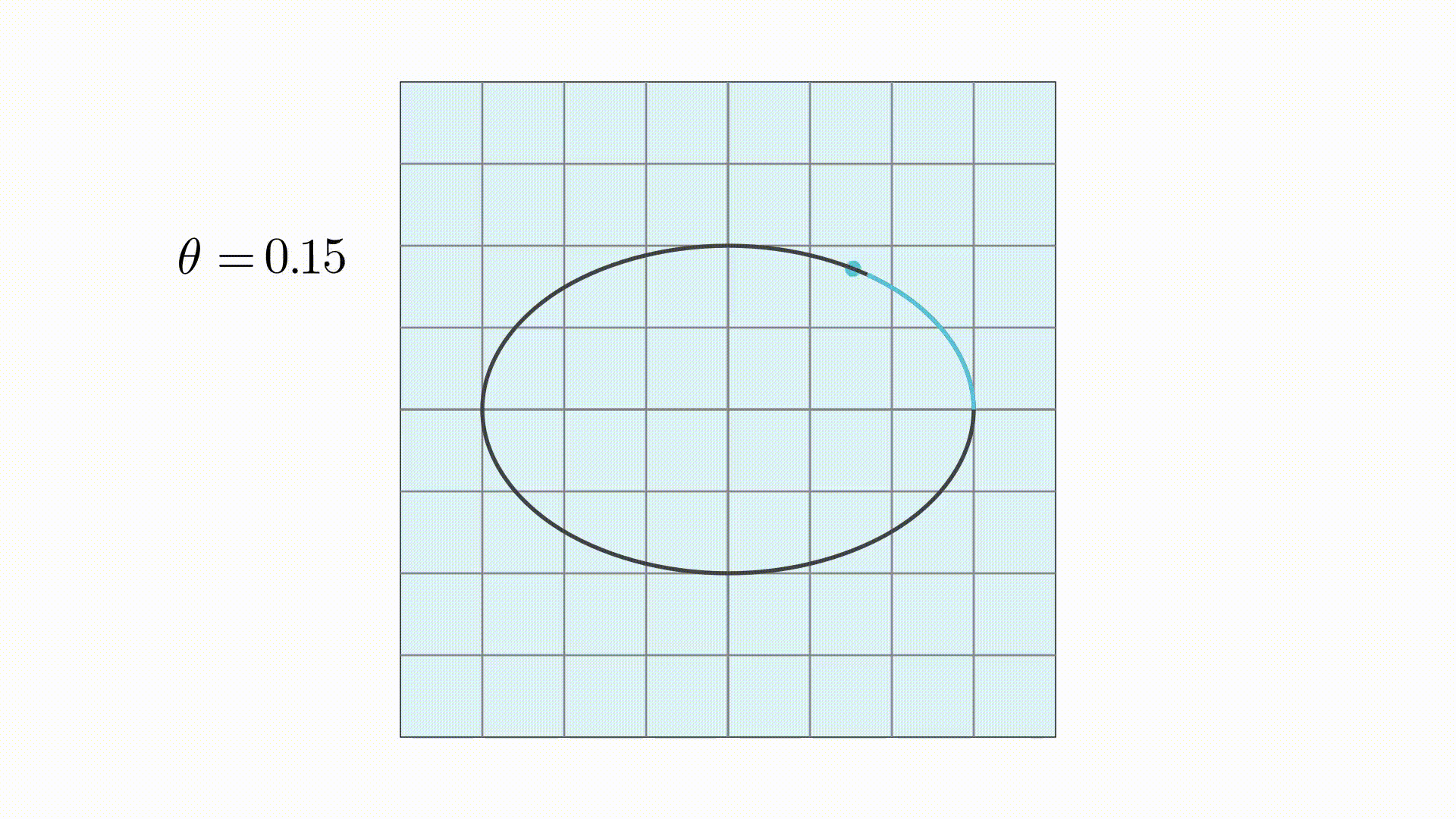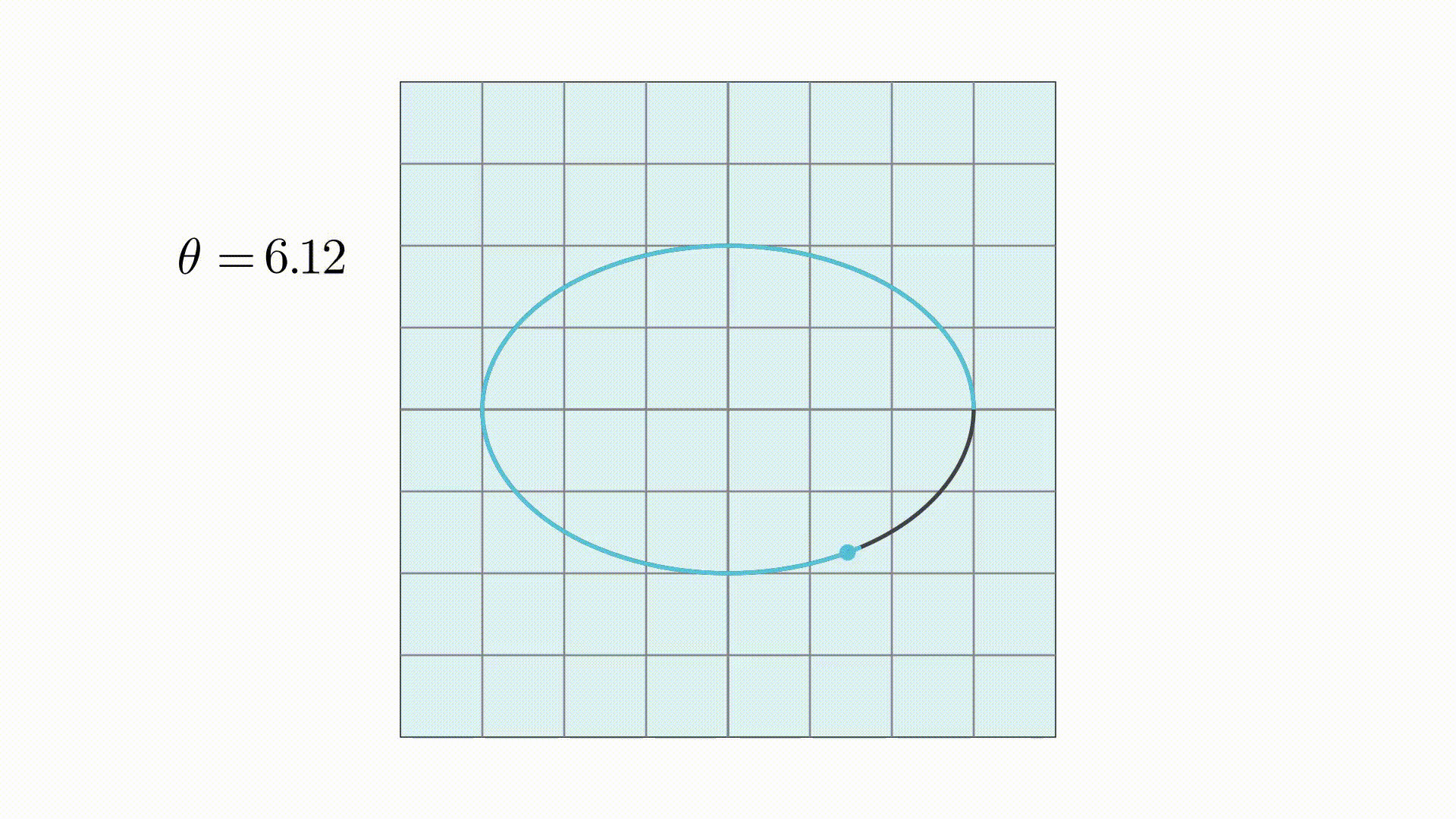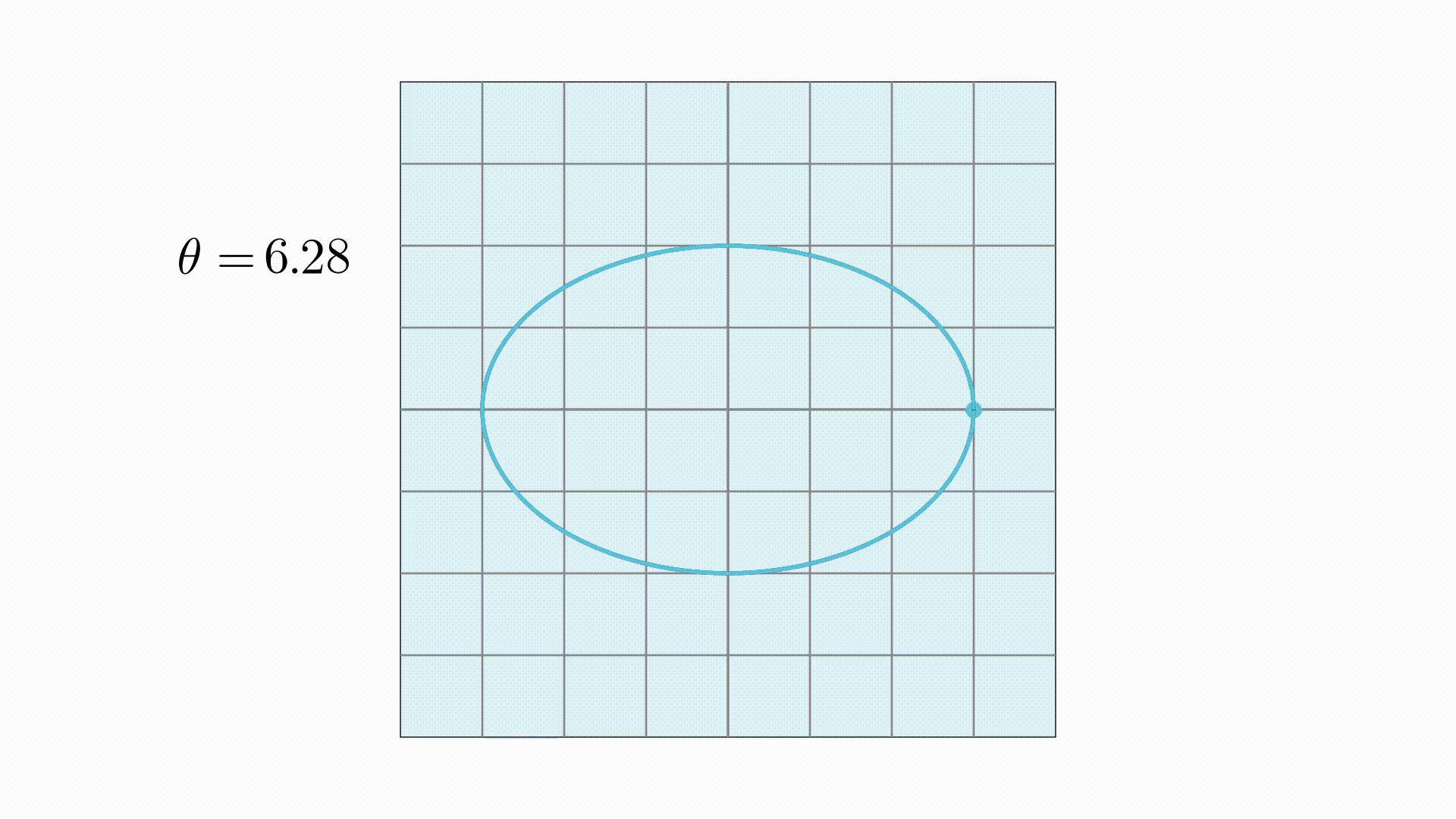
圆和椭圆现在都已经写成向量形式了,下面就还剩下映射矩阵需要求解
4 求解矩阵
要求解这个矩阵,还是要回到单位圆变椭圆的思路上来
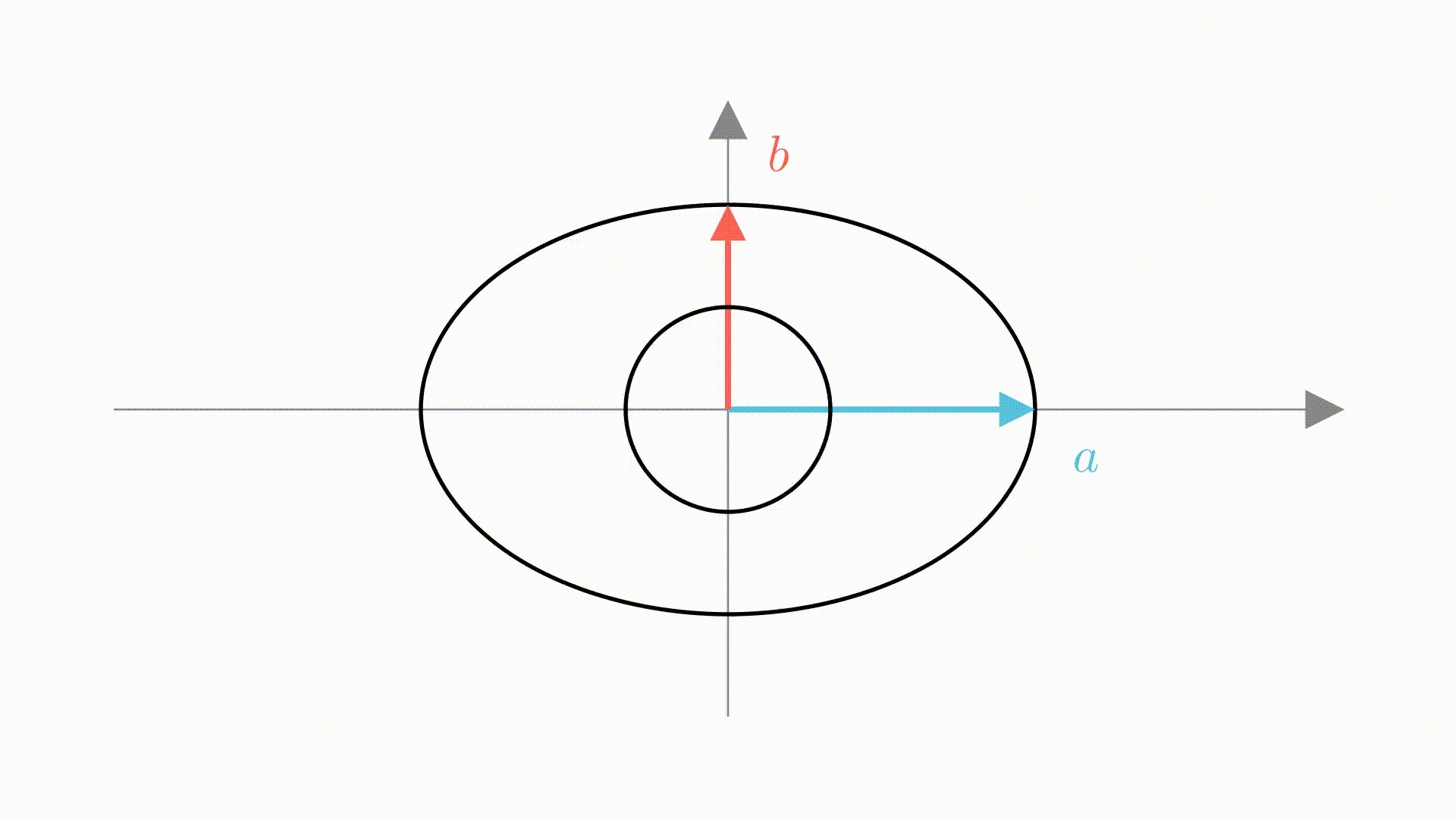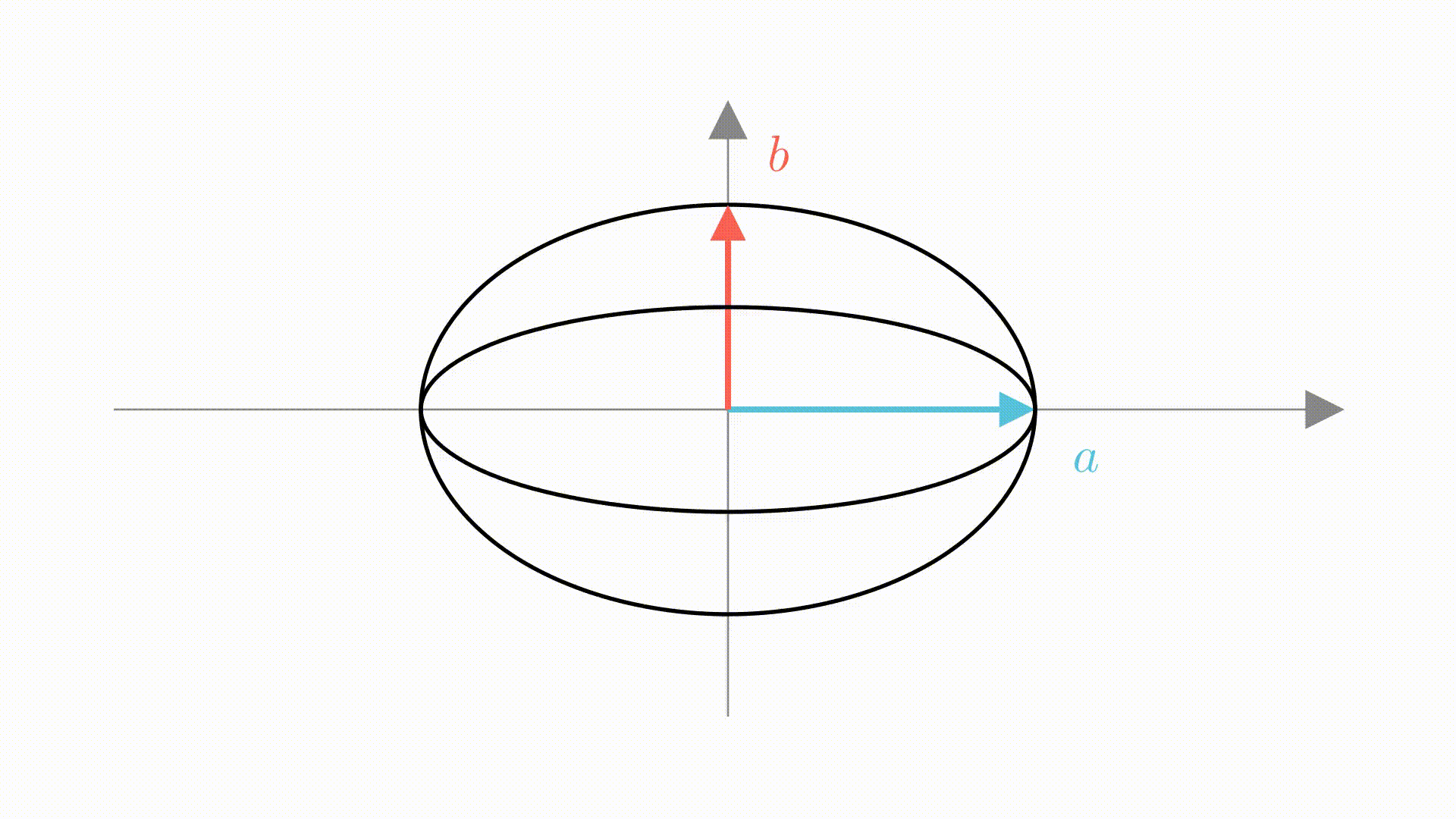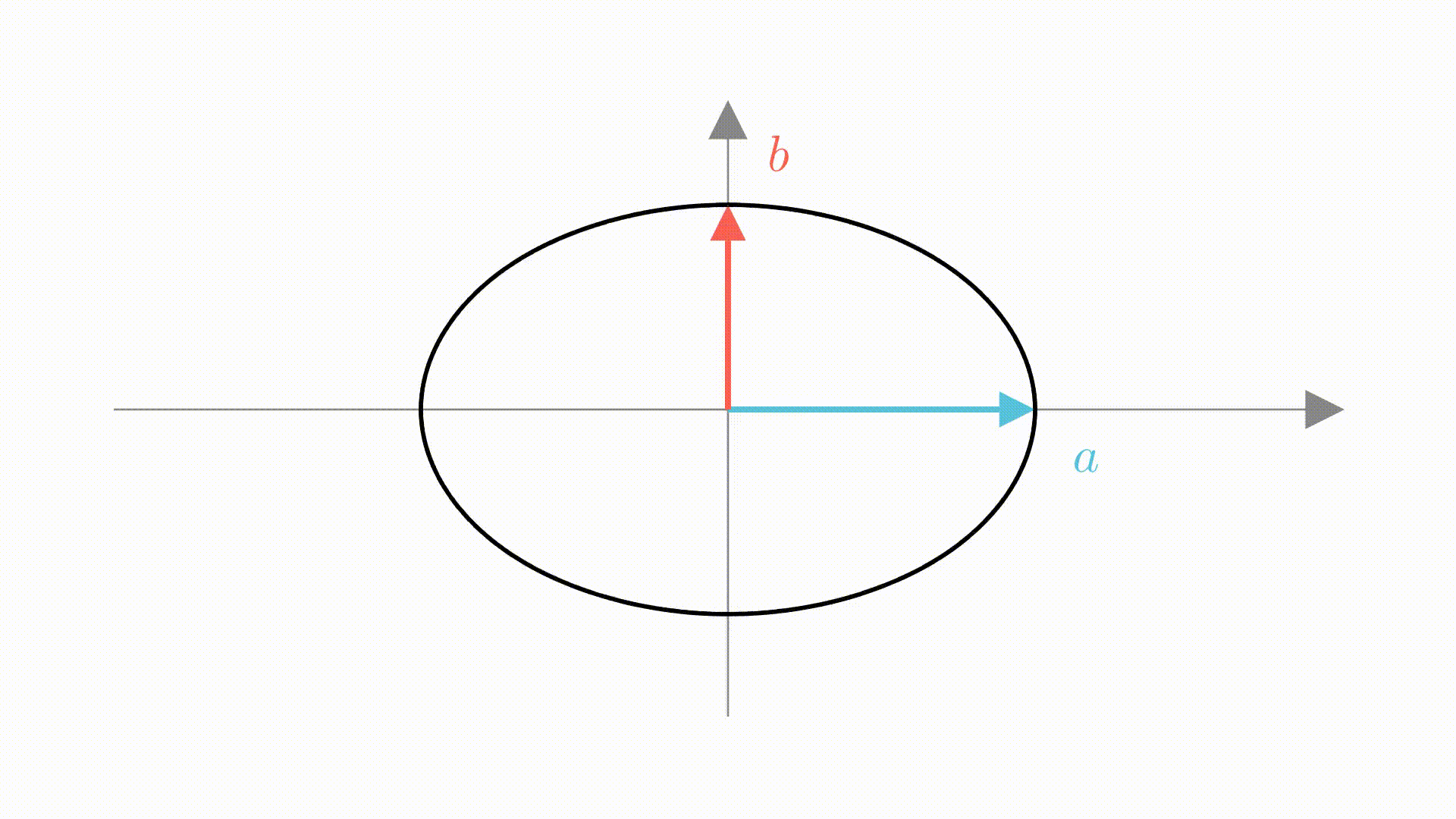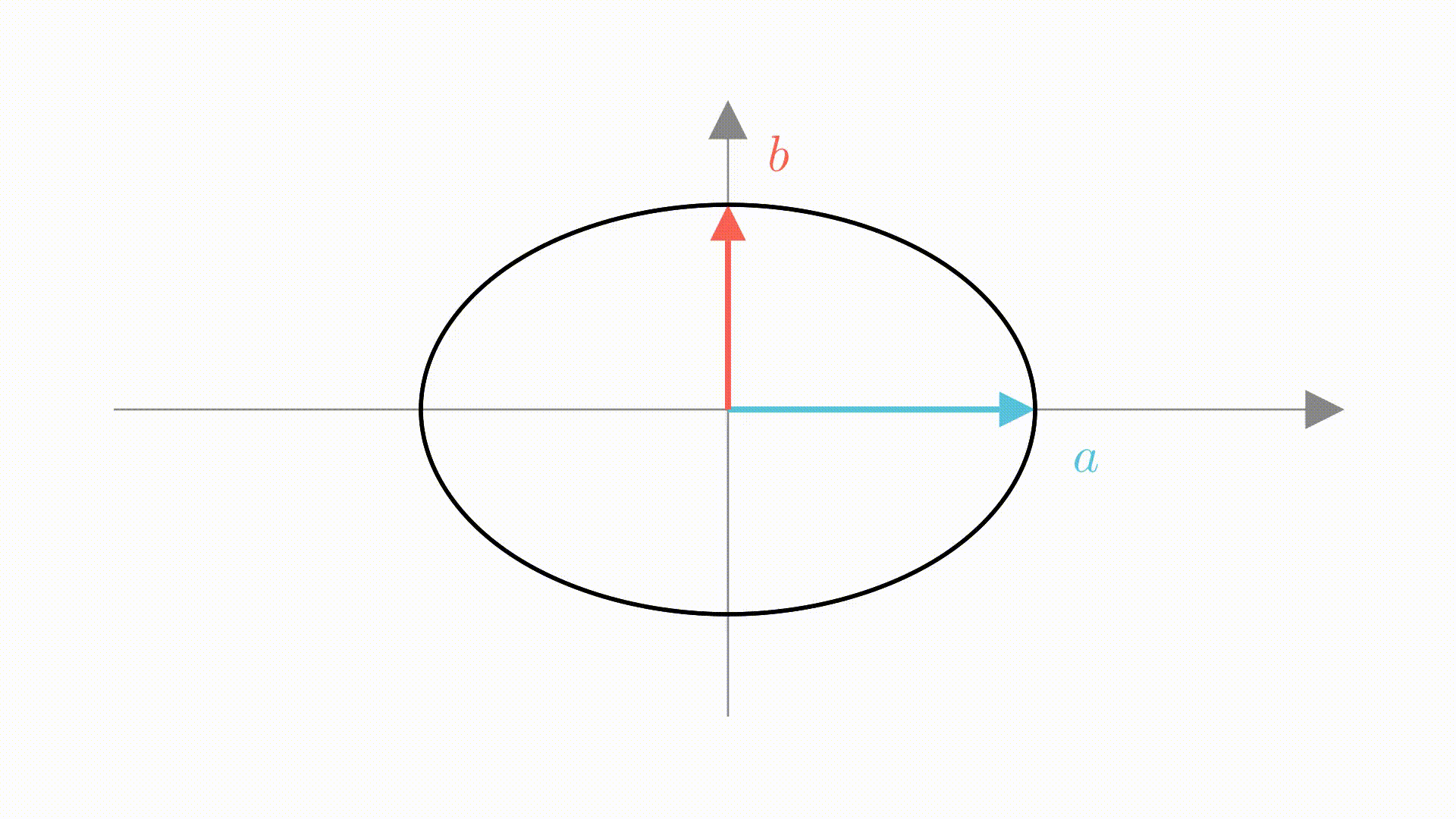
可以看到,这个变化过程分为两步,第一步是在横向上拉长 倍,第二步就是在竖直方向上拉长
倍

这样,很容易看出两次变换所用的矩阵

继而求出变换矩阵
将它作用在单位圆上,得到的结果和刚刚椭圆的表达式相同。
这再次说明了变换矩阵就是
5 结论
最后,根据行列式的几何意义可知

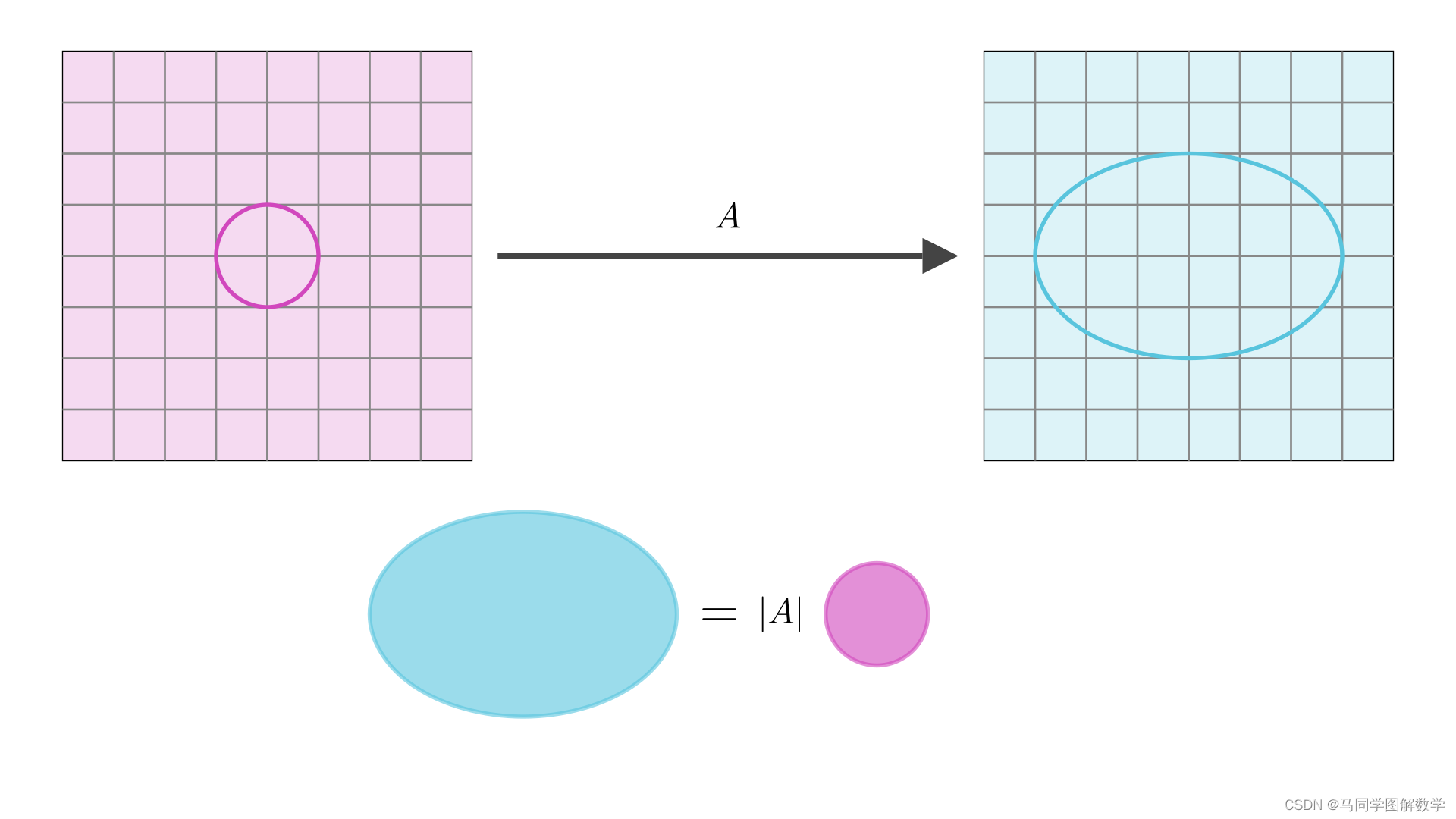
将 ,单位圆面积=
带入上式可得
![]()
百个故事,千幅图片,万名同学,欢迎加入:
首页-马同学图解数学-淘宝网淘宝, 店铺, 旺铺, 马同学图解数学 https://matongxue.taobao.com/
https://matongxue.taobao.com/

























 2017
2017

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










