python实现单目视觉手眼标定

最新推荐文章于 2024-08-21 03:44:16 发布

大大大管的笔记本

最新推荐文章于 2024-08-21 03:44:16 发布

阅读量2.3k

点赞数 9

文章标签：计算机视觉 matlab python opencv Powered by 金山文档

本文链接：https://blog.csdn.net/cg1135217680/article/details/129793146

版权

本文主要参考机械臂手眼标定原理及代码_绿竹巷人的博客-CSDN博客中的内容。手眼标定的原理比较简单主要为几个坐标系的转换。其中，包括的坐标系有：机械臂基坐标系、机械臂末端法兰坐标系、相机坐标系、棋盘格坐标系。有的地方会将机械臂末端法兰坐标系写为末端关节坐标系。

在以上4个坐标系中，已知的有：机械臂基坐标系到机械臂末端法兰坐标系的转换关系（通常可以从机械臂的示教器中读取参数，参数包括末端法兰的位置X，Y，Z，和转角RX，RY，RZ。部分示教器中RX和RZ的位置不太一样。）、相机坐标系到棋盘格坐标系的转换关系（可以通过OpenCV中的cv2.findChessboardCorners()函数去找到棋盘格，在经过cv2.cornerSubPix()函数获得较为准确的亚像素坐标。）

但是经过作者的测试及资料查阅，cv2.findChessboardCorners()函数的鲁棒性较低，经常检测不到棋盘格。所以作者采用了另外一种笨办法，就是通过Matlab中的工具包calibrateCamera经行标定。由于作者比较懒，所以具体的流程可以查看matlab单目相机标定_matlab 单目相机标定_Yoyo_wym的博客-CSDN博客。标定完成后，在导出的参数中有两项，分别为TranslationVectors和RotationVectors。这两项分别为平移向量和旋转向量。

在手眼标定时，通常使用的为X，Y，Z和RX，RY，RZ，所以需要将旋转向量变为旋转矩阵，这里可以使用cv2.Rodrigues()函数，其中的第一项则为旋转矩阵。代码如下：

rotMat = cv2.Rodrigues(rot_vector)[0]

之后只需要将选装矩阵与平移向量堆叠，形成坐标系之间的变换矩阵即可。代码如下：

def get_RT_from_chessboard(rot_vector, trans):
    rotMat = cv2.Rodrigues(rot_vector)[0]  # 旋转矩阵
    t = np.array([[trans[0], trans[1], trans[2]]]).T  # 平移向量
    RT = np.column_stack((rotMat, t))
    RT = np.row_stack((RT, np.array([0, 0, 0, 1])))
    return RT

完成以上操作后，将所有的相机坐标系到棋盘格坐标系的转换矩阵与机械臂基坐标系到机械臂末端法兰坐标系的转换矩阵分别存入两个不同的列表中。最后使用cv2.calibrateHandEye()函数完成标定即可。

（手眼标定的代码我放到最后啦）在完成手眼标定后，可以将旋转矩阵转换为角度值，便于观察正确与否。代码如下：

def isRotationMatrix(R):
    Rt = np.transpose(R)
    shouldBeIdentity = np.dot(Rt, R)
    I = np.identity(3, dtype=R.dtype)
    n = np.linalg.norm(I - shouldBeIdentity)
    return n < 1e-6


# Calculates rotation matrix to euler angles
# The result is the same as MATLAB except the order
# of the euler angles ( x and z are swapped ).
def rotationMatrixToEulerAngles(R):
    assert (isRotationMatrix(R))

    sy = math.sqrt(R[0, 0] * R[0, 0] + R[1, 0] * R[1, 0])

    singular = sy < 1e-6

    if not singular:
        x = math.atan2(R[2, 1], R[2, 2])
        y = math.atan2(-R[2, 0], sy)
        z = math.atan2(R[1, 0], R[0, 0])
    else:
        x = math.atan2(-R[1, 2], R[1, 1])
        y = math.atan2(-R[2, 0], sy)
        z = 0

    return np.array([x, y, z])

最后是python代码运行结果：

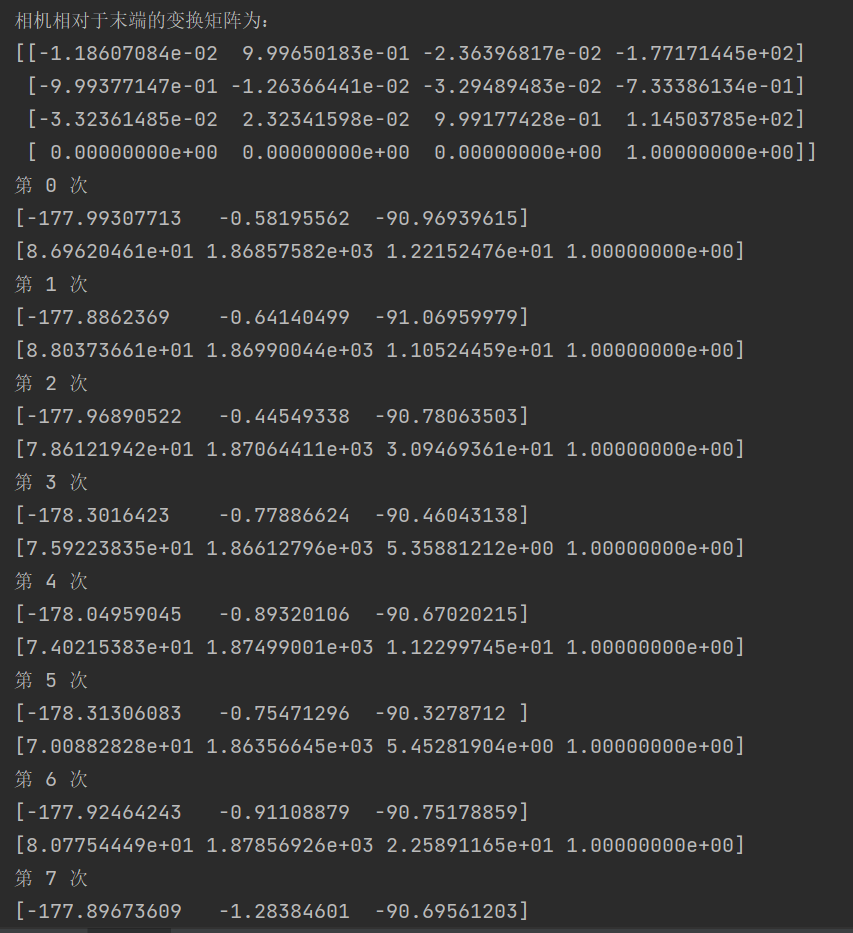
结果波动有一点大，主要是实验环境与设备精度较差。大家可以使用自己的数据运行一下。

（作者有一个疑问，就是为什么去掉几组对应数据后，运行结果相差非常大。希望有了解的大佬能够指点一二，万分感谢！）

全部代码：

import cv2
import numpy as np
from math import *
import math

robot_pose = [
    [1111.4, 11.1, 939.0, 178.7, 24.8, -177.0],
    [1047.7, 38.4, 911.4, 178.1, 28.0, -177.7],
    [1613.9, 299.4, 977.3, 169.5, 0.9, -160.7],
    [1487.5, -413.8, 980.9, -170.1, 9.6, 159.9],
    [1627.6, 41.9, 1069.3, -152.9, -1.5, -172.5],
    [1675.6, -569.4, 916.5, -171.7, -1.0, 149.3],
    [1814.6, 507.2, 916.5, -172.6, -16.4, -148.5],
    [1478.2, 243.4, 784.0, -147.4, -3.3, -155.3],
    [1311.4, -225.5, 697.7, -154.4, 24.7, -178.0],
    [1113.0, 105.6, 710.2, -154.2, 25.7, -155.0],
    [1154.9, 129.5, 705.2, 147.3, 31.0, 163.5],
    [1161.5, -4.3, 720.7, 171.0, 30.0, 172.1],
    [1109.0, -348.2, 710.9, -159.1, 37.1, 173.6],
    [1100.0, 18.0, 667.3, 173.2, 36.9, 177.3],
    [1065.1, 275.5, 667.3, 162.9, 39.1, -178.7],
    [1180.1, 129.1, 736.5, 135.4, 25.9, 160.3],
    [1285.0, 101.2, 810.3, 160.5, 21.3, 173.3],
    [1684.9, -164.7, 929.5, 173.1, -4.7, 172.5]]


rot_vector = np.array([[-0.444331639458419, -0.0541260870257246, -0.0191249342808060],
                       [-0.498694721737044, -0.0429388290593750, -0.0286855724870977],
                       [0.00566497406831067, -0.337577298507657, -0.152985926504062],
                       [-0.152067201622377, 0.363740570748545, 0.208582003808436],
                       [-0.0290826756496817, -0.124386546921850, 0.499606986176714],
                       [0.0396745975228313, 0.532743861541838, 0.145732463055067],
                       [0.228552594665488, -0.556510762759657, 0.247254032370080],
                       [-0.0886984906655996, -0.419225126413703, 0.602959893205377],
                       [-0.442137722665699, 0.0858118289158190, 0.443727274262198],
                       [-0.542053686596180, -0.327209135850706, 0.352376979298558],
                       [-0.581785170074419, 0.106379814755955, -0.468129120193672],
                       [-0.518950323499053, 0.0833672042262501, -0.110160108533779],
                       [-0.622358488964318, 0.221553902287258, 0.388221686317718],
                       [-0.633278794626946, 0.00350525694897012, -0.0912909997371519],
                       [-0.660043130264035, -0.128297998155833, -0.280889805194221],
                       [-0.531484445563775, 0.132334001838803, -0.671171897393355],
                       [-0.370397287972575, 0.0362460662049982, -0.303904912710458],
                       [0.0855293818191622, 0.136205282046175, -0.103892499262157]]).reshape(-1, 3)

trans = np.array([[-155.405388722990, -106.078268431491, 1022.14975665523],
                  [-123.712853072269, -111.860358437396, 1046.43459316310],
                  [-154.445365276512, -87.9330202489112, 832.657238265044],
                  [-61.9944877157222, -90.4090889406150, 977.717856307818],
                  [-62.2115497420955, -54.6506774350972, 914.440789618146],
                  [-92.3322702669019, -94.0108407177934, 949.138408249031],
                  [-73.7773093801483, -54.2970684680801, 829.080167053132],
                  [11.6609669255245, -90.3470790389651, 701.975535844775],
                  [-56.2136451427087, -108.858292148859, 755.432063184990],
                  [-88.1148353270807, -123.653251520512, 853.302557307283],
                  [-102.311918737224, -23.5244610290553, 843.664884217409],
                  [-87.3307158163044, -80.5646326895448, 838.946713657157],
                  [-31.4150116587646, -96.4488544605512, 953.381802217281],
                  [-126.819368393301, -56.3042323816518, 851.545743686402],
                  [-93.0147369487899, -71.0498239463426, 897.759976687940],
                  [-159.005601716752, 3.28143854480163, 844.527943710107],
                  [-91.9519688463492, -69.9728538555509, 821.179493778495],
                  [-151.250287977788, -60.1207007913382, 782.272363557195]
                  ]).reshape(-1, 3)


# 用于根据欧拉角计算旋转矩阵
def myRPY2R_robot(x, y, z):
    Rx = np.array([[1, 0, 0], [0, cos(x), -sin(x)], [0, sin(x), cos(x)]])
    Ry = np.array([[cos(y), 0, sin(y)], [0, 1, 0], [-sin(y), 0, cos(y)]])
    Rz = np.array([[cos(z), -sin(z), 0], [sin(z), cos(z), 0], [0, 0, 1]])
    R = np.dot(np.dot(Rz, Ry), Rx)
    return R


# 用于根据位姿计算变换矩阵
def pose_robot(z, y, x, Tx, Ty, Tz):  # 注意输入顺序！！！！！！
    """
    Args:
        x: x轴旋转角度
        y: y轴旋转角度
        z: z轴旋转角度
        Tx: Tx为平移横坐标
        Ty: Ty为平移纵坐标
        Tz: Tz为平移高坐标
    Returns: 旋转矩阵与平移矩阵的叠加，即两坐标系之间的转换矩阵
    """
    thetaX = x / 180 * pi
    thetaY = y / 180 * pi
    thetaZ = z / 180 * pi
    R = myRPY2R_robot(thetaX, thetaY, thetaZ)
    t = np.array([[Tx], [Ty], [Tz]])
    RT1 = np.column_stack([R, t])  # 列合并
    RT1 = np.row_stack((RT1, np.array([0, 0, 0, 1])))
    return RT1


# 用来从棋盘格图片得到相机外参
def get_RT_from_chessboard(rot_vector, trans):
    rotMat = cv2.Rodrigues(rot_vector)[0]
    t = np.array([[trans[0], trans[1], trans[2]]]).T
    RT = np.column_stack((rotMat, t))
    RT = np.row_stack((RT, np.array([0, 0, 0, 1])))
    return RT


def isRotationMatrix(R):
    Rt = np.transpose(R)
    shouldBeIdentity = np.dot(Rt, R)
    I = np.identity(3, dtype=R.dtype)
    n = np.linalg.norm(I - shouldBeIdentity)
    return n < 1e-6


def rotationMatrixToEulerAngles(R):
    assert (isRotationMatrix(R))

    sy = math.sqrt(R[0, 0] * R[0, 0] + R[1, 0] * R[1, 0])

    singular = sy < 1e-6

    if not singular:
        x = math.atan2(R[2, 1], R[2, 2])
        y = math.atan2(-R[2, 0], sy)
        z = math.atan2(R[1, 0], R[0, 0])
    else:
        x = math.atan2(-R[1, 2], R[1, 1])
        y = math.atan2(-R[2, 0], sy)
        z = 0

    return np.array([x, y, z])


good_picture = [i for i in range(18)]

# 计算标定板到相机的变换矩阵
R_all_chess_to_cam_1 = []
T_all_chess_to_cam_1 = []
for i in good_picture:
    chess2cam_RT = get_RT_from_chessboard(rot_vector[i].T, trans[i].T)

    R_all_chess_to_cam_1.append(chess2cam_RT[:3, :3])  # 旋转矩阵
    T_all_chess_to_cam_1.append(chess2cam_RT[:3, 3].reshape((3, 1)))  # 平移向量

# 计算法兰末端位姿与相机的变换矩阵
R_all_end_to_base_1 = []
T_all_end_to_base_1 = []
# print(sheet_1.iloc[0]['ax'])
for i in good_picture:

    end2robot_RT = pose_robot(robot_pose[i][3], robot_pose[i][4], robot_pose[i][5],
                              robot_pose[i][0], robot_pose[i][1], robot_pose[i][2])

    R_all_end_to_base_1.append(end2robot_RT[:3, :3])
    T_all_end_to_base_1.append(end2robot_RT[:3, 3].reshape((3, 1)))

# 手眼标定
R, T = cv2.calibrateHandEye(R_all_end_to_base_1, T_all_end_to_base_1, R_all_chess_to_cam_1, T_all_chess_to_cam_1)
RT = np.column_stack((R, T))
RT = np.row_stack((RT, np.array([0, 0, 0, 1])))  # 即相机到机械臂末端法兰变换矩阵
# RT = np.linalg.inv(RT)
print('相机相对于末端的变换矩阵为：')
print(RT)

chess2base_T = []
chess2base_theta = []

# 固定的棋盘格相对于机器人基坐标系位姿不变，对结果验证，原则上来说，每次结果相差较小
for i in range(len(good_picture)):
    RT_end_to_base = np.column_stack((R_all_end_to_base_1[i], T_all_end_to_base_1[i]))
    RT_end_to_base = np.row_stack((RT_end_to_base, np.array([0, 0, 0, 1])))

    RT_chess_to_cam = np.column_stack((R_all_chess_to_cam_1[i], T_all_chess_to_cam_1[i]))
    RT_chess_to_cam = np.row_stack((RT_chess_to_cam, np.array([0, 0, 0, 1])))

    RT_cam_to_end = np.column_stack((R, T))
    RT_cam_to_end = np.row_stack((RT_cam_to_end, np.array([0, 0, 0, 1])))

    RT_chess_to_base = RT_end_to_base @ RT_cam_to_end @ RT_chess_to_cam  # 即为固定的棋盘格相对于机器人基坐标系位姿不变
    RT_chess_to_base = np.linalg.inv(RT_chess_to_base)

    chess2base_T.append(RT_chess_to_base[:, -1])
    chess2base_theta.append(RT_chess_to_base[:3, :3])

# 棋盘格相对于机械臂基座标XYZ不变，对结果验证
for i in range(len(chess2base_T)):
    print('第', i, '次')
    print(rotationMatrixToEulerAngles(chess2base_theta[i]) / np.pi * 180)
    print(chess2base_T[i])
    print('')