路径跟踪算法之模型预测控制(MPC)跟踪

路径跟踪算法之模型预测控制(MPC)跟踪

1.MPC简介

模型预测控制（以下简称 MPC）是一种依赖于系统模型进行数学优化的复杂控制器。它利用优化算法计算有限时间范围内一系列的控制输入序列，并优化该序列，但控制器仅执行序列中的第一组控制输入，然后再次重复该循环。MPC 主要分为 3 个关键步骤：模型预测、滚动优化、反馈校正。

2.MPC在轨迹跟踪过程中的应用

在轨迹跟踪应用领域，通常 MPC 建模可根据机器人的控制方式选择基于运动学运动状态方程建模或者基于动力学运动状态方程建模。前者是根据车辆转向的几何学角度关系和速度位置关系来建立描述车辆的运动的预测模型，一般只适用于低速运动场景；后者是对被控对象进行综合受力分析，从受力平衡的角度建模，一般应用在高速运动场景，如汽车无人驾驶。本文基于双轮差速运动学模型，推导实现差速运动的MPC轨迹跟踪控制。 双轮差速运动学线性 MPC 轨迹跟踪实现的基本思路是状态方程–线性化–离散化–预测方程–约束线性化–非线性目标函数转为二次规划–求解最优问题。其中线性化可采用泰勒级数展开忽略高次项的方式，离散化可采用后向差分法，这两个部分都有一定的模型精度丢失。

3.推导过程

3.1双轮差速运动学建模
首先，以双轮中心点作为参考点建立双轮差速运动学状态方程：

其中状态量为[x,y,z]T,控制量为:[v,w]T。
式 3-1 为非线性方程，角度和位置存在耦合关系，为了便于逻辑计算与后续
结果解算，在期望位置点采用一级泰勒展开进行近似线性化处理：

其中:

式 3-2 减去式 3-3 后得到：

其中：

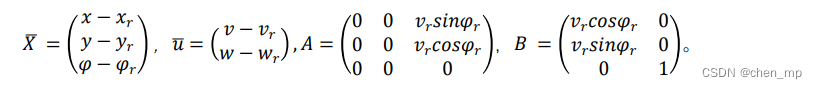
线性化完成之后，形成连续的线性运动学模型，为了在控制周期内编程实现，再采用欧拉前项差分法将模型离散化：

变换得：

整理得离散化的线性表达式：


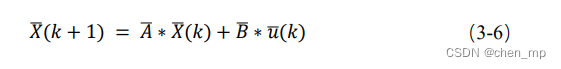
其中$\overline{\text{A}}$ = (I + TA)，$\overline{\text{B}}$ = TB，$\overline{\text{A}}$， B