后端状态估计-卡尔曼滤波器理解+扩展-SLAM14讲笔记(六)

最新推荐文章于 2022-12-13 15:10:35 发布

Stu.xian

最新推荐文章于 2022-12-13 15:10:35 发布

阅读量1k

点赞数 2

分类专栏： slam 文章标签：人工智能机器学习

本文链接：https://blog.csdn.net/chuangkeiss/article/details/127443820

版权

slam 专栏收录该内容

11 篇文章 4 订阅

订阅专栏

文章目录

系列文章目录
前言
一、pandas是什么？
二、使用步骤
- 1.引入库
- 2.读入数据

状态估计的概率解释：位姿x和路标y服从某种概率分布，目的是通过某些运动数据u（比如惯性测量传感器IMU输入）和观测数据z（比如拍摄到的照片像素点的值）来确定状态量x和y的分布。

首先我们回顾一下SLAM过程中的运动方程和观测方程：假设在t=0到t=N的时间内，有位姿 $\boldsymbol{x}_{0}$ 到 $\boldsymbol{x}_{N}$ ，并且有路标 $\boldsymbol{y}_{1}, \cdots, \boldsymbol{y}_{M}$ ，则可以写成数学模型为：

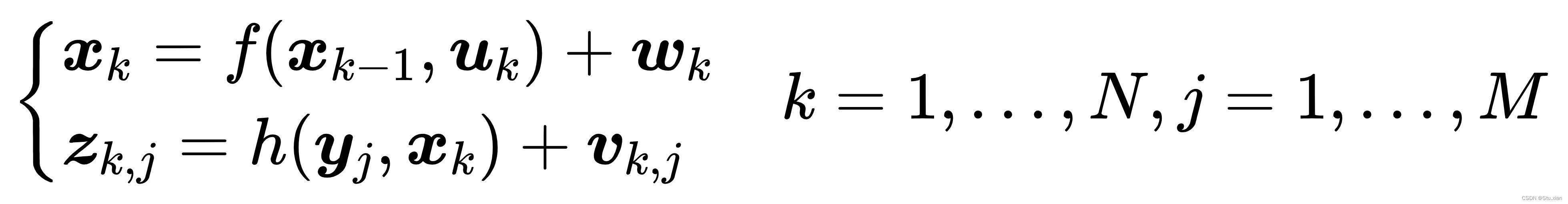
1.值得注意的是在运动方程中（可以理解为机器人从k-1时刻到k时刻，位置x的变化）uk是运动传感器的数据的输入，wk为该过程中加入的噪声。当机器人在xk位置上看到某个路标yi时，产生了一个观测数据 $z_{k,j}$ (即观测数据依赖位置与路标)， $v_{k,j}$ 为观测噪声.虽然这个很简单，但所有的工作围绕这个方程展开的，所以再提一遍。

2.在观测方程中，只有在 $x_{k}$ 看见了 $y_{i}$ 时，才会产生观测数据，否则就没有，事实上在某一位置特征点的数量众多，实际中观测方程会远远大于运动方程。

由于位姿和路标点是待估计量，我们令 $x_{k}$ 为k时刻所有的未知量，他包含了相机位姿和m个路标： $\boldsymbol{x}_{k} \stackrel{\text { def }}{=}\left\{\boldsymbol{x}_{k}, \boldsymbol{y}_{1}, \ldots, \boldsymbol{y}_{m}\right\}$ ，同时k时刻所有的观测数据为 $z_{k}$ 则：

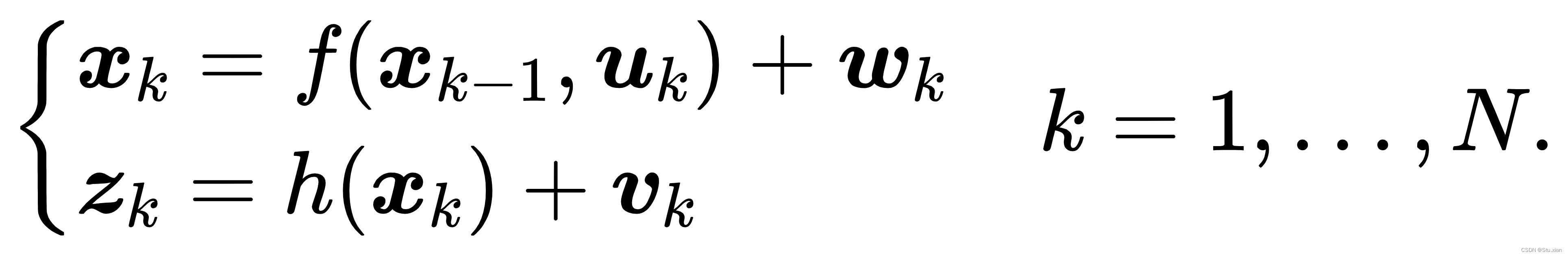
第k时刻是，我们希望用过去0到k时刻中的数据来估计现在的状态分布：

根据贝叶斯法则有：

对于前面非线性优化忘了的，感觉一头雾水。我们可以先从根源了解一下贝叶斯法则：

这时我们先看一下上式子所包含的意义：

这里根据贝叶斯公式直观看书上应该简化了，让人很难容易理解，中间应该有一部分。具体我也是参考这个博主

SLAM14讲学习笔记（六）后端（最难一章：卡尔曼滤波器推导、理解以及扩展）

$P\left(\boldsymbol{x}_{k} \mid \boldsymbol{x}_{0}, \boldsymbol{u}_{1: k}, \boldsymbol{z}_{1: k}\right) \$ 后验：根据0~k时刻所有的数据，来得到当前的状态。

$P\left(\boldsymbol{z}_{k} \mid \boldsymbol{x}_{k}\right)$ 似然：给定了一个先验Xk的情况下，什么观测数据Zk最能符合这个先验“的概率。（由观测方程可得）

$P\left(\boldsymbol{x}_{k} \mid \boldsymbol{x}_{0}, \boldsymbol{u}_{1: k}, \boldsymbol{z}_{1: k-1}\right)$ 先验：是根据0~k-1时刻的观测数据，推测得知k时刻的先验状态（对于这个，里面的u作为一个传感器数据，其实可以忽略掉它，因为0~k-1时刻的数据不应该包含uk，但是本书里面着重要讲的是视觉SLAM，u应该指的是惯性逻辑单元IMU之类的数据，如果只依靠观测的图像来判断状态的话，忽略掉u就行了）

后验概率 = 似然 * 先验。

以k-1时刻为条件概率展开：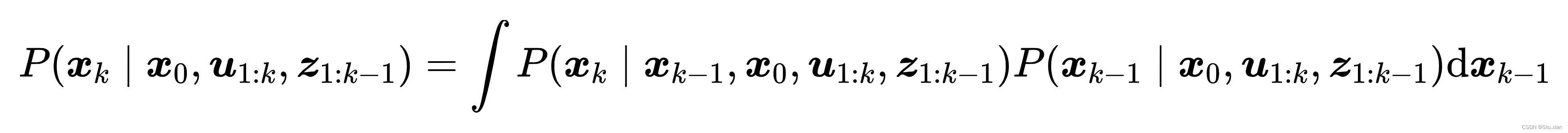

全概率公式

我们现在考虑的是渐进式问题，即k时刻的状态与k-1时刻状态有关（马尔科夫性质）。这样我们就可以得到扩展卡尔曼滤波（EKF）为代表的滤波器方法。

当前时刻状态只和上一个时刻有关，右侧（指的是那个积分）第一部分可进一步简化:

这里，由于k时刻状态与k-1之前的无关，所以就简化成只与k-1和 uk有关的形式，与k 时刻的运动方程对应。第二部分可简化为

先假设状态量都服从高斯分布，扩展卡尔版滤波是非线性的，在此之前我们首先线性的卡尔曼滤波谈起，线性高斯是指运动方程和观测方程可以由线性来描述：

并假设这里的噪声服从零均值高斯分布：

考虑随机变量，另一变量y满足：

其中A,b为线性变量的系数矩阵和偏移量, w为噪声项,为零均值的高斯分布 $\boldsymbol{w} \sim N(\mathbf{0}, \boldsymbol{R})$ 。

现在，利用马尔可夫性，假设我们知道了k -1时刻的后验(在k-1时刻看来）状态估计ag-1及其协方差P-1，现在要根据k时刻的输入和观测数据，确定x的后验分布。为区分推导中的先验和后验，
以上帽子cx。表示后验，以下帽子c表示先验分布，
卡尔曼滤波器第一步，通过运动方程确定 $x_{k}$ 的先验分布（线性）：

这一步称为预测，它显示了如何从上一个时刻的状态，根据输入信息（但有噪声）推断当前时刻的状态分布，这个分布也就是先验。记：

由观测我们可以计算在某个状态改下应该产生怎样的观测数据：

此时我们根据公式来推出后验，假设后验的概率分布为 $\boldsymbol{x}_{k} \sim N\left(\hat{\boldsymbol{x}}_{k}, \hat{\boldsymbol{P}}_{k}\right)$ ，则：

已知等式两侧都是高斯分布，那么只需比较指数分布，无需理会前面的因子部分。（由附录A.1）

现在我们将指数部分展开，有：

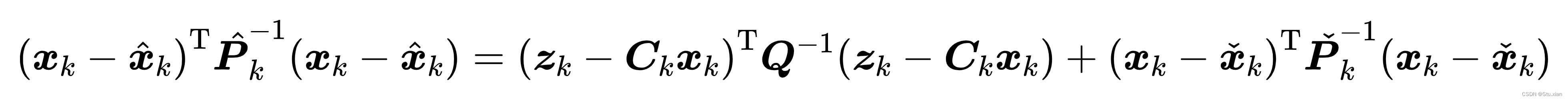
1.这时突然出现 $\hat{\boldsymbol{x}}_{k}$ 和，公式太多会有点分不清楚了：

（遗留问题）

2.这里我们捋一下怎么推导过来的，第一次我也没怎么看懂。 $x_{k}$ 可以表示任意状态，我们在前面定义了路标和位姿，在k时刻这个状态是服从高斯分布的。 $\hat{\boldsymbol{x}}_{k}$ 为它的均值（这里表示后验） $\hat{\boldsymbol{P}}_{k}$ 为它的协方差（后验）。

然后对公式进一步推导：

现在我们整理一次项和二次项，对于二次系数我们可得到：

该式给出了协方差的计算过程。为了便于后面列写式子，定义一个中间变量:

于是就有：

同理比较一次项系数，有：

整理（取系数并转置）得

在整理得到：

此时我们就得到了后验均值的表达。根据书上我们再总结一下：

1.预测：

2.更新,先计算K，又称为卡尔曼增益:

然后计算后验概率分布：

至此我们推导了经典的卡尔曼滤波器的整个过程。

Stu.xian

关注

2
点赞
踩
1

收藏

觉得还不错? 一键收藏
0
评论
后端状态估计-卡尔曼滤波器理解+扩展-SLAM14讲笔记(六)

是根据0~k-1时刻的观测数据，推测得知k时刻的先验状态（对于这个，里面的u作为一个传感器数据，其实可以忽略掉它，因为0~k-1时刻的数据不应该包含uk，但是本书里面着重要讲的是视觉SLAM，u应该指的是惯性逻辑单元IMU之类的数据，如果只依靠观测的图像来判断状态的话，忽略掉u就行了）现在，利用马尔可夫性，假设我们知道了k -1时刻的后验(在k-1时刻看来）状态估计ag-1及其协方差P-1，现在要根据k时刻的输入和观测数据，确定x的后验分布。为区分推导中的先验和后验，此时我们就得到了后验均值的表达。
复制链接

扫一扫