滑模控制几种趋近率的对比（hm-2）

我们以最简单的牛顿第二定律作为被控对象来进行几种趋近率的对比。

 

滑模面设计为：

 

e(t)为期望位置和实际位置的差，则有：

 分别采用等速趋近率、指数趋近率以及幂次趋近率：

 

 

代入得到：

 

在指数趋近中,趋近速度从较大值逐步减小到零,不仅缩短了趋近时间,而且使运动点到达切换面时的速度很小。单纯的指数趋近，运动点逼近切换面是一个渐近的过程，不能保证有限时间内到达，切换面上也就不存在滑动模态了，所以要增加一个等速趋近项，使当s接近于零时，趋近速度是ε而不是零，可以保证有限时间到达。为了保证快速趋近的同时削弱抖振,应在增大k的同时减小ε。

幂次趋近率通过调整α值，可保证当系统状态远离滑动模态(s较大)时,能以较大的速度趋近于滑动模态，当系统状态趋近滑动模态(s较小)时,保证较小的控制增益,以降低抖振。

为了进行比较，取m=1，c1=1期望位置x=3，初始位置x=0

等速趋近率：

 

 指数趋近率

 

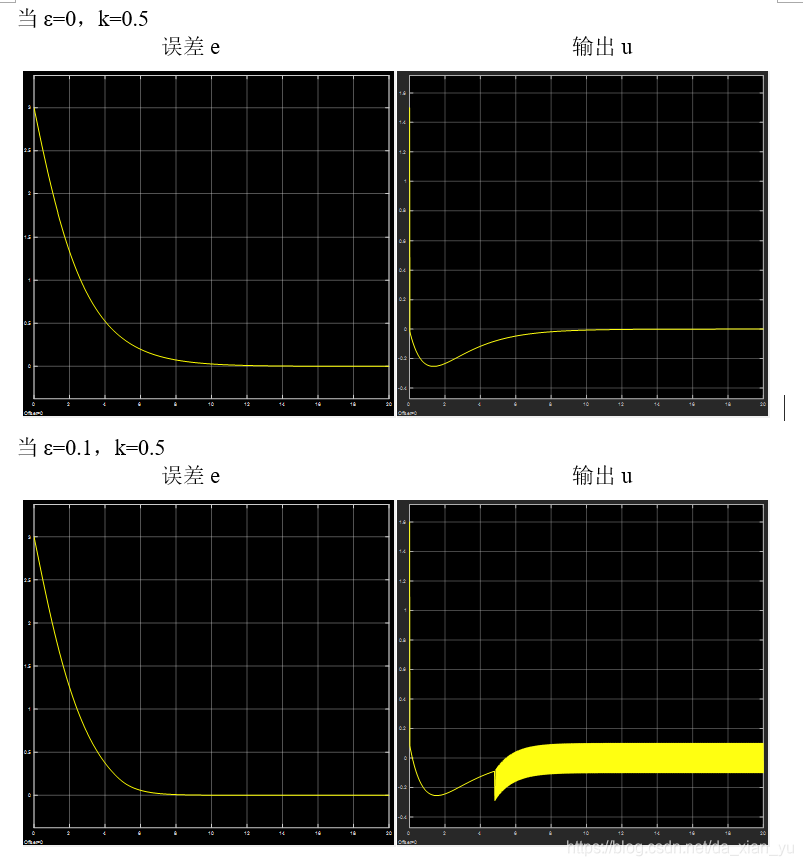
幂次趋近率