使用IMU进行状态估计及进阶

Feisy

已于 2022-09-14 10:12:25 修改

阅读量4.2k

点赞数 5

分类专栏：机器人文章标签：状态估计

于 2022-02-08 11:18:18 首次发布

本文链接：https://blog.csdn.net/feisy/article/details/122820265

版权

机器人专栏收录该内容

16 篇文章 4 订阅

订阅专栏

文章目录

前言
基本思想
一姿态估计
二姿态估算与滤波的关系
三贝叶斯滤波-核心内容(by忠厚老实的老王）
四贝叶斯滤波和其他滤波的关系
五卡尔曼滤波
六扩展卡尔曼滤波
七无痕卡尔曼滤波
八粒子滤波
madgick的姿态估算分析
流形上的卡尔曼滤波
不变卡尔曼滤波
自动驾驶方面的滤波建议-by忠厚老实的老王
- 图优化
- 非线性优化

前言

本文章将汇总我这么长时间来，使用IMU进行姿态估计的总结，所以会很多内容，并且不能够一次性完成。我会分成很多次，一步步介绍下去。
目前的计划是，从零开始介绍姿态估算，然后进一步介绍姿态估算与滤波的关系，然后介绍各个我知道的进阶算法。

本文将采用状态估计，而不是姿态估计。因为姿态估计的范围比较狭小，是状态估计中的一部分，后续可能会介绍状态估计中的位置，速度等估计。

基本思想

状态估计=计算公式+数据

首先，我们需要知道的是，给你一些传感器的数据，我们怎么根据这些数据来计算得到姿态？这个就是计算公式的作用。
有了公式以后，我们需要更好的数据来进行更精准的估计，所以，我们需要滤波。

一姿态估计

几乎所有姿态估计的资料都是大篇幅的介绍滤波什么的，不讲姿态估计和滤波有什么鬼关系。
原因是因为，对于各种姿态估计的计算方法来说，一旦原理确定了，姿态估计的计算公式是比较固定的，所以重心就变成了怎么去获取更精切的数据。
在实际运用中的开发也是如此，可能姿态估计计算一行代码就完了，剩下的代码都是进行滤波的。

这部分主要是记录一些姿态估计的计算方法的。

1.1 通过6轴IMU来进行姿态估计的入门级方法

下面的方法只需要简单的三角函数以及反三角函数就可以进行姿态估计：
看本文尾部参考资料[1]。
我在geek-workshop看到Malc发了翻译过的文章，见[2]

1.1.1 通过加速度计计算姿态

该公式的原理是通过计算重力在各个方向上的分量，通过反三角函数就可以计算得到姿态：Racc=[Axr,Ayr,Azr]

Axr = arccos(Rx/R)
Ayr = arccos(Ry/R)
Azr = arccos(Rz/R)

1.1.2 引入陀螺仪来得到更好的姿态估计

加速度计已经告诉我们Axr，Ayr，Azr的倾角，为什么还要费事去得到陀螺仪的数据？答案很简单：加速度计的数据不是100%准确的。有几个原因，还记加速度计测量的是惯性力，这个力可以由重力引起（理想情况只受重力影响），当也可能由设备的加速度（运动）引起。因此，就算加速度计处于一个相对比较平稳的状态，它对一般的震动和机械噪声很敏感。这就是为什么大部分的IMU系统都需要陀螺仪来使加速度计的输出更平滑。但是怎么办到这点呢？陀螺仪不受噪声影响吗？
陀螺仪也会有噪声，但由于它检测的是旋转，因此对线性机械运动没那么敏感，不过陀螺仪有另外一种问题，比如漂移（当选择停止的时候电压不会回到零速率电压）。然而，通过计算加速度计和陀螺仪的平均值我们能得到一个相对更准确的当前设备的倾角值，这比单独使用加速度计更好。

You might be asking yourself by this point, if accelerometer model already gave us inclination angles of Axr,Ayr,Azr why would we want to bother with the gyroscope data ? The answer is simple: accelerometer data can’t always be trusted 100%. There are several reason, remember that accelerometer measures inertial force, such a force can be caused by gravitation (and ideally only by gravitation), but it might also be caused by acceleration (movement) of the device. As a result even if accelerometer is in a relatively stable state, it is still very sensitive to vibration and mechanical noise in general. This is the main reason why most IMU systems use a gyroscope to smooth out any accelerometer errors. But how is this done ? And is the gyroscope free from noise ?

The gyroscope is not free from noise however because it measures rotation it is less sensitive to linear mechanical movements, the type of noise that accelerometer suffers from, however gyroscopes have other types of problems like for example drift (not coming back to zero-rate value when rotation stops). Nevertheless by averaging data that comes from accelerometer and gyroscope we can obtain a relatively better estimate of current device inclination than we would obtain by using the accelerometer data alone.

使用陀螺仪的方法：陀螺仪估计姿态=使用估计姿态+陀螺仪测得的角速度*dt
对于陀螺仪来说，它衡量的是角速度，理论上如果我们将角速度进行积分，可以得到姿态，但因为精度，误差以及计算的问题，实际上这样子做得到的结果是十分差的。
但是，我们认为，陀螺仪长时间累积下来的结果，是跟我们估计的姿态接近的，与其进行积分计算，我们用估计的姿态作为陀螺仪累积的结果更好。
因此，我们在预测的姿态基础上，加上角速度乘以时间的变化，从陀螺仪中得到了一个新的姿态：Rgyro=[RxGyro ,RzGyro,RzGyro]

RxGyro = RxEst(n-1)+Rotx*T
RyGyro = RyEst(n-1)+Roty*T
RzGyro = RyEst(n-1)+Rotz*T

这样，我们引入了陀螺仪的测量数据，如果加速度计的数据有巨大误差，通过陀螺仪的数据，可以将估计的误差降低。

上面的公式只是演示，具体的实现涉及从估计的姿态中反算出RxEst等，看[1],[2]

现在我们有了两个姿态,怎么做呢？加权组合得到新姿态

Rest(n) = (Racc * w1 + Rgyro * w2 ) / (w1 + w2)

1.2 四元数解算姿态角解析

可以参考著名的《An efficient orientation filter for inertial and inertial/magnetic sensor arrays》

~~我的解读文章~~

二姿态估算与滤波的关系

2.1 状态方程和观测方程

在这里插入图片描述

2.2 数据和滤波的关系

我们计算姿态的公式是理想的，只要数据足够准确，计算出来的结果就很好。
但是现实是，只要有测量，就会有误差。
误差包括仪器本身自带的偏差，外部环境的影响，计算的精度损失等等。
怎么获取更精确的数据，是个十分难的问题。

获取更精确的数据，这是滤波的目的，滤波的作用是让数据遵循的分布的误差变小

记 x是我们感兴趣的数据，x遵循某种分布f(N,delta),delta是指分布的方差

通过滤波来获得更精准的数据的步骤：

使用滤波算法对数据的分布f(N,delta)（记住，是数据的分布，不是数据），使其方差越来越小（方差变小，则误差变小）

方差变小之后，我们就可以根据分布来计算数据的值，比如说像下面的求均值方法：

如果是高斯分布，则可以从分布中获取。

滤波和状态数据的关系：真实的数据的分布是隐藏的，状态方程和观测方程都只是状态数据的来源，我们根据这两种类型的数据，通过滤波，可以计算得到数据的分布，然后通过迭代，让这个分布的方差（即误差）越来越小，从而越来越精准。

在这里插入图片描述

记住，将状态方程和观测方程都看成只是带了信息的数据来源，两者都不是最佳的数据。

三贝叶斯滤波-核心内容(by忠厚老实的老王）

3.0 贝叶斯公式：核心思想是通过先验概率和似然概率计算得到的后验概率的方差比前两者更小（方差小意味着误差小）

https://www.bilibili.com/video/BV1Yq4y1E7BU/?spm_id_from=333.788.recommend_more_video.6
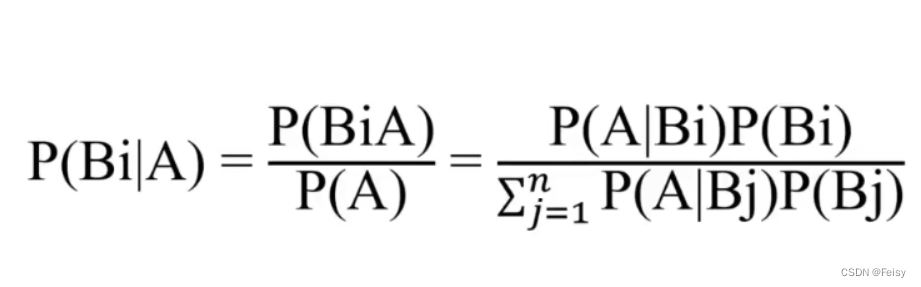
在这里插入图片描述

贝叶斯率滤波的思想：新信息出现后的B的概率=B概率 * 新信息带来的调整
至于为什么 A 事件发生后导致的调整为P(A|B)/P(A),这就需要代数了，推导也不复杂.(没有找到推导过程，暂且默认它是对的)

3.1 条件概率

3.1.1 条件概率的定义

在这里插入图片描述
这里跟我们理解的有点不一样，我们一般认为，条件的意思是加上了限制，概率会变得更小。
但经常条件概率下反而经常增大。

原因是，样本空间发生了变化。没有条件时总样本空间是S，有条件时样本空间是A。很好
帮助理解的例子是后面的例子1。

3.1.2 条件概率的图示讲解

图示一
S是样本空间
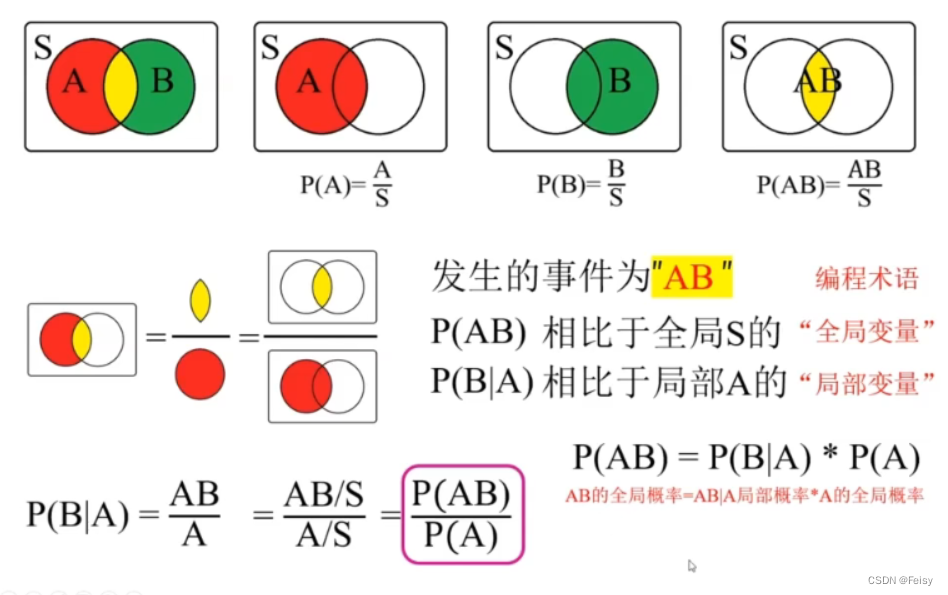
在这里插入图片描述
在条件概率下，样本空间发生变化了，不能在原来的S上讨论，要在A的基础上进行讨论

3.1.3 条件概率的例子

例子一
1 背景
一个女孩子去参加相亲，有100个男嘉宾供她选择。你也是其中一个。假设每个人被选中的
概率是相同的。而女孩没有任何条件，则你被选中的概率为1/100

2 条件概率的情况
如果女孩加上身高180，有房有车，工作在北上广，则只有5个人符合条件，你是其中之一。
则你被选中的概率是1/5.

加上条件概率以后，需要关注的范围从100，减到5，大大缩小了范围，更有助于做判断.

3.2 全概率公式与贝叶斯公式

3.2.1 全概率公式

在这里插入图片描述

3.2.2 贝叶斯公式

在这里插入图片描述

3.3 贝叶斯公式的简单运用例子

在这里插入图片描述
tips:我做的答案不一定准

因为第一个球是红球，所以条件A限定在第一，二个盒子了。
抽了一个红球出来，，还剩下2红1白，从这三个中抽取一个红球的概率是2/3

P(A) = 1/2
P(AB)=1/5(白红，红白，红红，白白)

P(B|A)=P(AB)/P(A) = (1/5)/(1/2) = 2/5

3.4 贝叶斯滤波的三大概率

在这里插入图片描述

1 主观概率（先验概率）：试验之前的概率，可以猜一个概率，并认为它是对的。特点就是没有做试验，就定了一个概率

2 后验概率：猜测了一个值后，然后观测，在观测值的条件下，猜测的值为真实值的概率 P(B|A),A猜测的值，B是观测的的值

3似然概率:源自最大似然估计，表示哪个原因最有可能导致了结果，一般用来表示测量的准确度（传感器）

似然举例：
A班99男1女，B班99女1男
我们随机抽一个班，再随机抽一个人进行观测，结果是女。
此女最像是从B班抽取出来。

我的观测结果是女的，那么是什么原因导致了这个结果？
最大似然的意思就是这个女孩是最有可能从B班抽取的,因为B班的女的太多了。

3.5 离散随机变量的贝叶斯滤波

3.5.1 定义以及公式

A 事件发生后,B发生的概率 P(B|A)=P(BA)/P(A)

A,B用x,y表示，那就变成了如下的形式：
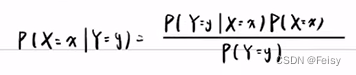
在这里插入图片描述

3.5.2 例子温度的预测

温度的先验概率：也就是我们主动给的一个概率

在这里插入图片描述

测量温度

在这里插入图片描述

后验概率

在这里插入图片描述

看看公式里面的成分：

先验概率：

后验概率(测量在后）：

似然概率(测量在前)：

一个常量值：P(T_m=10.3)表示测量值为10.3的概率。
这里会有个疑问，这个值已经是测量出来的了，已经发生了的，那它的概率是1? 答案是：不是的。
随机变量的取值和它的概率不是一个概念。比如说抛硬币，正面朝上，它的概率是0.5,而
不是1.
P(T_m=10.3)是随机试验的一个结果而已，
随机变量的取值是一次随机试验可能的结果。
随机变量的分布律代表对随机变量的不确定的刻画。
即：随机变量的取值和随机变量的分布律没有任何关系

P(T_m=10.3)的计算方法：
用全概率公式来算：

先验概率是猜的，在我们给出的时候，它就已经定了。
似然概率是跟仪器相关的，当我们拿出一个温度计时，它的似然概率就已经定了。
因此
P(T_m=10.3)是一个常数。

改写一下上面得到的后验概率的公式，将P(T_m=10.3)用一个常数n来表示
在这里插入图片描述

怎么求n=P(T_m=10.3)? 所有后验概率加起来就可以了，因为：
在这里插入图片描述
而后验概率之和为1：
由此可得：

3.6 连续随机变量的贝叶斯公式

3.6.1 错误的公式套用

如果我们根据离散型的贝叶斯公式来套用连续性随机变量的公式，会得出下面的公式：
在这里插入图片描述
这样子直接套用，会有两个问题：

对于连续性随机变量来说，单个值发生的概率为0，因此下面的表达式是0，也就是上式中的分母是0

下面这种形式的似然概率是从未定义过的，不符合条件概率的形式。

3.6.2 正确的连续型随机变量的贝叶斯公式推导

思路：化积分为求和

在这里插入图片描述

基于上面的基础，我们就可以将连续型随机变量的贝叶斯公式，用离散型的那种公式表达出来：

上式还有个问题就是，这种形式会导致分子，分母都是0，也无法计算。
严格上说，分子分母不是0，是无穷小，所以可以写成极限的形式。

使用中值定理可得：

进一步化简：

3.6.3 后验概率的贝叶斯公式

在这里插入图片描述

写成离散型的那种形式：

3.7 似然概率与狄拉克函数

3.7.1 从测温度的例子说起

大写的X代表系统的状态，大写的Y表示观测值

先验概率：数学期望是10，方差为1的标准正态分布作为先验概率,X=10是最有可能的温度。
方差是对猜测的结果的不确定的刻画。如果猜测非常自信，方差可以小，如果不自信，方差可以给大点。
因此，此处方差为1，表示真实的温度在9-11度之间

使用温度计测量温度：

如果有似然概率的计算公式，就可以计算后验概率了。
但是，似然概率怎么写？
真按照概率密度函数PDF的计算方法，就要对上面的式子求导：

求导结果是0。因为这是关于x,y的函数，一积分，y就没了。这时，方程只是关于x的函数，对这个x的函数求导y，就变成了0了。
这显然不是我们想要的

这里要利用一个小技巧：将似然概率密度公式乘以一个很小的值
因此，似然概率密度就变成：
上面的表达式的含义就是代表了传感器的精度

上面那句话怎么用概率的方式来表达呢？如下：

在这里插入图片描述

表示温度计测量的温度落在[x-0.2,x+0.2]的概率是1，它等价于

这个说的就是传感器的精度，表示温度计观测到的值落在真实值x上下0.2的概率很大，100%。

对于上面例子的图示：就是[x-0.2,x+0.2]的曲面积分是1，那条红色的竖线，就是我们要算的概率密度

那么似然概率具体的值是多少呢？很遗憾，具体的值是不知道的。因为一般来说，传感器只会给你
[-0.2,0.2]类似这样一个精度的范围，但它不会给你更多的信息。根据这个信息，只能推导出积分是多少，不能推导出那条红色竖线代表的值是多少。

存在问题：无法根据已有信息，精确求得似然概率的值。

3.7.2 似然概率模型

针对上面未解决的问题，我们自己给似然概率假设其遵循的模型，它会有什么样的形式。然后根据这个模型，就可以计算似然概率的值，就可以继续往下算了。

3.7.2.1 等可能模型

等可能型的意思是，在真实值给的的范围内，每个值出现的概率是相等的。

这意味着Y是服从均匀分布的,因此概率密度是个常数：
常数是最好积分的，比如上面3.7.2的温度例子中，面积的积分是1，我们将概率密度的值C代入：
可以求得C=2.5
这样子，似然概率函数的求值函数如下：

3.7.2.2 阶梯模型

阶梯模型，意味着传感器的精度是分段的。越靠近真实值，可能性就比较高。

跟上面均匀分布模型相似，我们可以计算得到概率密度函数：

阶梯模型有个非常重要的推广：直方图模型，用常数形式的离散模型来表示非常复杂的非线性模型。

根据直方图模型，可以诱导出直方图滤波（非线性卡尔曼滤波的一种，与粒子滤波起名）

3.7.2.3 正态分布（最常用）

正态分布的话，就会导致[x-0.2,x+02]的积分是小于1：

正态分布的似然概率：

正态分布有个好处，均值和方差比较好控制

3.7.3 有了似然概率模型之后的测温度例子

先验概率：

似然概率：
似然概率模型使用正态分布，精度为[-0.2,0.2]>

后验概率：
后验概率=常数 x 先验概率 x 似然概率

具体算一下后验概率

3.7.4 计算结果总结：贝叶斯滤波可以让方差显著降低，不确定度减少。这表明滤波有效，滤掉了噪声

对比一下计算结果

先验方差：1，似然方差：0.2² -------->后验方差：0.038²

3.7.5 上面计算过程复杂，由此引出一个重要定理

假设：先验概率和似然概率服从正态分布。
先验概率服从以下分布：

似然概率服从以下分布：

则后验概率为：

上面公式的解读：

方差大的占的权重就小（方差代表了预测的误差，方差更大，意味着更不准确，就给个小的权重，反之亦然）
随着计算的迭代，方差会越来越小。

证明：
暴力证明，可以用Mathematica算

极端情况一：先验概率的方差远大于似然概率的方差

极端情况二：先验概率的方差远小于似然概率的方差

两种情况结合起来得到结论：

方差的变化规律总结：

上面的式子，分母总是大于1，则意味着：

方差会越来越小，也就是不确定不断降低。
先验概率即使给的很不准，但是如果观测概率准确，就可以越来越靠近真实值。
即使先验概率和似然概率方差大，都不准，意味着初值和观测都不准，但是经过滤波后，后验概率也会变得准一些。这是一个非常好的性质。

3.7.6 狄拉克函数

3.7.6.1 狄拉克函数的定义：服从正态分布的似然概率方差趋于0时的形式

在这里插入图片描述

狄拉克函数性质一：在数学期望处是无穷大，其他地方是0（下面的公式表示数学期望是0）

狄拉克函数性质二：从负无穷到正无穷的积分是1。因为它也是概率密度，也要满足归一化

狄拉克函数性质三：选择性（最重要的性质）

3.7.6.2 引入狄拉克函数的目的：处理传感器无限精确的问题

如果传感器的概率密度分布函数的方差是0，则它的概率密度函数就是狄拉克函数

3.7.6.3 狄拉克函数的本质：离散的必然事件的概率密度

例子：
P（x=0）=1，是一个离散的随机变量，是个必然事件。将其连续化：

它的分布图像即使一个单位阶跃函数，在0处发生阶跃。
如果设：

则狄拉克函数是这个单位阶跃函数的导数：

3.7.6.4 狄拉克函数性质三：选择性的证明

用上一小节中的狄拉克函数是H(x)的导数代入到性质三的表达式：

使用复合函数的积分法则展开：

因为H(x)在负无穷的时候是0，在0处是1，上式可变成：

再对上面的公式使用牛顿-莱布尼茨公式并化简可得：

3.7.6.5 狄拉克函数的一些推论

推论1（需要积分区间包含0）

证明思路，证明[负无穷，a],[b,正无穷]的积分都是0，因为概率密度的和要满足所有概率之和为1，就证明了(a,b)的积分是1

推论2（需要积分区间包含0）

推论3

3.7.6.6 狄拉克函数在贝叶斯滤波的运用

对上面的概率密度进行积分

这个实际上是一个必然事件，在X=10的时候，Y=10，它的概率是1.这表示传感器的精度是无限的，测量所得温度就是真实值。

3.8 随机过程的贝叶斯滤波-重要

滤波的三个步骤：

1 给定一个先验概率

2 观测,得到似然概率

3 根据先验概率和似然概率，计算后验概率

3.8.1 随机过程存在的难点

在这里插入图片描述

1 有多个随机变量，彼此之间可能不独立

2 每个随机变量，有多个观测值。意思是我们会进行多次 [确定先验概率-观测-计算后验概率] 这样的迭代

3.8.2 多次迭代中，变量的先验概率的给定

一通过猜测给初值。

x0~xk这k次迭代的先验概率，每次都使用猜测值，就是随便猜一个值给它们.
这样子做会有缺点：
过于依赖观测，等于是直接放弃掉了预测的信息
比如说，有如下两个随机过程：

如果我们通过猜来给定初值，方程包含的信息就被舍弃掉了，因为我们只是靠猜来给值，方程给出的信息没有用上。这样子做，导致我们只能靠观测来滤波。
能写出随机过程的方程，即使建模不准，也是可以部分反映出一些信息的。猜测初值的行为就把这部分信息丢掉了。

二只有x0的初值是猜的，从x1~xk次迭代的先验概率是递推出来的。
好处：1 保留了随机过程的一些特性
这种方法也是贝叶斯滤波使用的。

递推怎么做？

3.8.3 贝叶斯滤波使用[状态方程-观测方程]这样的方式来做递推

3.8.3.1 状态方程：x_k = f(x_k-1)+Qk,Qk是预测噪声

状态方程是一种建模方式，表示xk与xk-1是什么关系
比如说，有这么一个状态方程：
xk = (1/2)*g * t^2 +Q,Q是摩擦或者阻力之类的随机扰动。

对上式进行泰勒展开到一阶,就得到xk和xk-1的关系：
在这里插入图片描述

一个很现实的问题：现实中大量的问题是写不出上面那种精确的表达式。比如说下面的曲线

这个曲线，你写不出xk和xk-1的关系。

上面问题的解决方法：
随便写一个：
随着而来的疑问：这样随便写真的好吗？
贝叶斯滤波在于融合。
先验是对问题的感性认知和经验所得。
而观测是数据，带来新的信息。
贝叶斯滤波融合这两个东西。当先验给得很差，几乎不带有信息，贝叶斯滤波仍然可以通过观测数据，估算出一个大概的东西。

幸运的是，我们还是能给很多问题的状态方程写出一个大概的表达式，有表达式就会带来信息，贝叶斯滤波就有用武之地。

3.8.3.2 观测方程：Yk=h(Xk)+Rk,反映了状态是如何引起传感器的读数,Rk是观测噪声

有时候，传感器感应的不一定是我们感兴趣的状态的直接数据，而是关于这些状态的函数的数据。
观测直接跟状态相关的例子：
我们想测的是温度，那么状态就是温度，而传感器则是温度计，观测的也是温度，观测值可能是Yk=Xk+Rk 这样的形式，直接跟状态有关
观测不是直接跟状态相关的例子：
状态是位移，观测的是一个角度传感器，只能观测到角度，那观测的数据则可能是Yk=arcsin(xk)+Rk这种不是直接跟状态关联，而是需要经过运算的关系。

3.8.4 贝叶斯滤波的递推

3.8.4.1 错误的递推示例：无观测情况下的递推

假设有这么一个随机过程：
在这里插入图片描述
无Qk，表示建模完全准确。

我们来对这个随机过程做贝叶斯滤波的递推：

1 设置初值，给x0猜一个值：

这表示x0服从(0,1)的正态分布。

2 做递推

这样的递推不行！！！！！！！！！！！！！！！！！！！！！

失败的根源在于没有引入观测！！

3.8.4.2 正确的递推讲解

仍然使用上面的状态方程：
在这里插入图片描述

1 初始步：给x0设置初值：

2 预测步：根据xk-1,预测xk^- （就是根据状态方程推导出先验概率）:

3 更新步：根据观测值yk对预测步得到的xk^- 进行更新,得到xk⁺ （就是计算后验概率）

更新步也称为后验步

递推的图示：

无观测的情况下：上一步的先验概率就是下一步的先验概率

有观测的情况下：上一步的后验概率作为下一步的先验概率

3.8.5 贝叶斯滤波的递推的具体做法

本节的内容大量来自于：你真的搞懂贝叶斯滤波了吗？

3.8.5.1 问题的建模

(1) 符号定义：

(2) 问题描述:状态方程和概率的关系

(3)状态方程和观测方程:

(4) 一个会用到的定理: 条件概率里的条件可以做逻辑推导

3.8.5.2 预测步推导（求先验）：求概率密度函数

当前状态的概率密度函数:
在这里插入图片描述

要求解f_k，可以先求解P(X_k < x),求解方法类似与泰勒一阶展开，展开到上一时刻状态量

对于每个u的取值，有：P(u)用全概率公式展开：

对上式进行简单变形，括号里面的X_k=u，一边减去f(X_k-1),一边减去f(v), 也就是对中括号里面的条件做逻辑推导（看上面3.8.5.1的第四点），因为X_k-1=v,所以f(X_k-1) = f(v)

对上式整理一下，根据状态方程：X_k = f(X_k-1 )+Q_k ====>X_k - f(X_k-1 )=Q_k

Q_k和X_k-1是相互独立的（我们这样假设的前提），这样就可以把后半部分的条件拿掉
Q_k和X_k-1是相互独立的证明：见后面注解3

这样我们就得到了P(X_k=u)的表达式：

将P(X_k=u)的表达式代入到P(X_k < x)的表达式中

前面我们已经知道：概率密度函数f_k=dP(X_k<x)/dx

3.8.5.3 更新步推导（求后验）：概率密度函数

假设有一个传感器，在k时刻有观测 Y_k = y_k,我们需要利用观测值y_k去将f_k^-更新成f_k⁺

3.8.5.3.1 先计算似然概率的表达式

似然概率等于：

对条件概率里面的已知条件做逻辑推导：不等式y_k <Y_k <y_k +ε 同时减去h(X_k)

由于Y_k = h(X_k)+R_k====>R_k = Y_k - h(X_k)

因为R_k 和X_k 相互独立，我们就得到了似然概率的表达式：

证明R_k 和X_k 相互独立：见后面注解3

3.8.5.3.2 根据先验概率，似然概率计算后验概率

套用贝叶斯公式：

3.8.5.4 根据后验概率计算状态： $\hat{}$ x_k

这里递推的都是概率密度函数，要求各时刻的状态估计，只需要求均值即可。

如果是高斯分布，可以从分布中直接获取

3.8.5.5 贝叶斯滤波算法流程

在这里插入图片描述

3.8.5.6 推导的三条核心结果公式—记起来

1 先验概率推导结果公式

2 后验概率推导结果公式

3 后验概率推导结果公式中的η_k

它是后验概率的表达式的后半部分的积分的倒数

3.8.5.7 贝叶斯滤波算法优缺点

在这里插入图片描述

缺点的一些解决方案：

3.8.5.8一些注解

. 注解1 在这里插入图片描述

. 注解2：参考链接：利用定积分定义求极限的原理与套路，你会了吗？

. 注解3 :Q_k与x_k-1相互独立，:R_k与x_k相互独立
在这里插入图片描述

四贝叶斯滤波和其他滤波的关系

内容来自： https://blog.csdn.net/wq1psa78/article/details/106824921
在这里插入图片描述
这几种滤波里面，以卡尔曼滤波最为著名，虽然现在普遍认为图优化比滤波要好，但是滤波这种思想，还是值得学习的。

五卡尔曼滤波

上一节中，我们完整推导了贝叶斯滤波，从3.8.5.6小节的三条核心公式，我们可以发现，里面出现了好几个无穷积分，这在解决实际问题的时候，几乎是不可行的。
卡尔曼在贝叶斯的基础上，做了一些限定，来解决无穷积分的问题

5.1 卡尔曼滤波的前提假设

2.1小节给出了状态方程和观测方程，卡尔曼做了一个设定：
假设f(x_k−1),h(x_k) 为线性，Q_k,R_k为0均值正态分布,X_k−1服从正态分布：X_k−1 ~ N(μ⁺_k−1,σ⁺_k−1),这样，2.1小节的所以状态转移方程和观测方程可以写成：

F,H是常数

假设f,h是线性，以及Xk服从正态分布，这个很可能跟实际情况不符，这也是导致误差的根本来源之一。

按照贝叶斯滤波的步骤，我们接着进行 [预测-更新]这两步的实现

5.2 预测步

3.8.5.6小节中的先验概率的表达式

把相应的概率密度代进去积分可得：

积分的计算有两个方法，一个是通过软件Mathematica算，一个是手算，下面是手算的方法：

1 参考博客：高斯函数的傅里叶变换
2 时域卷积=频域乘积，如h=f*g（卷积），则G(h)=G(f)*G(g),G表示傅里叶变换， ↩︎

结论归纳

5.3 更新步

3.8.5.6小节中的后验概率计算公式：

将先验概率密度表达式和似然概率密度表达式代入上式计算可得：
计算的方法同5.2 预测步的计算

5.4 卡尔曼滤波五大公式归纳：

在这里插入图片描述

5.5 一些分析

5.5.1 参数大小造成的影响

对卡尔曼增益系数进行一些变形,将分子，分母同时除以σ^-_k：
K = hσ^-_k/(h²σ^-_k+R)= h/(h²+R/σ^-_k)

当R远大于σ^-_k时，K的值十分小，几乎为0，则μ⁺_k = μ^-_k，这意味着我们更相信预测。这是十分合理的，R是观测方差，σ^-_k是预测方差，R远大于σ^-_k，表示观测完全不可信，因此卡尔曼滤波的值会偏向于预测值
当R远小于σ^-_k时，K=1/h,μ⁺_k =y_k/h,而y_k=h x_k +R,而R比较小，从而μ⁺_k = x_k，这意味着，我们更相信观测值

5.5.2 矩阵形式的卡尔曼滤波

矩阵形式下：

μ_k ======> $\vec{μ }$ 是向量
方差 σ_k====>∑_k则是协方差矩阵
F,H都是矩阵

下图是有输入u的卡尔曼5大公式，状态返程多了Gu

5.5.3 马尔可夫与观测独立

在这里插入图片描述

5.6 总结

tips:正态分布具有封闭性，对正态分布进行卷积，相乘，归一化，还是正态分布。

卡尔曼的5个公式就没有什么先验概率，后验概率这些，也没有积分，就是普通的数的加减。这是一个非常好的性质。计算量也小。这就是正态分布比较好的性质带来的.
从上一个刻的后验概率，推导这一时刻的先验概率，是两个独立的正态分布相加，那就是卷积。卷积得到的分布，也是正态分布

后验概率=η_k *先验概率 * 似然概率，两个独立的正态分布相乘,结果也是正态分布

由此可见，卡尔曼滤波的操作都是在正态分布上进行的。正态分布只由期望，方差两个参数决定.
所以计算卡尔曼滤波，我们只需要计算期望和方差就可以了，就不用管先验概率，后验概率，积分这些了。
这也是计算量小的原因。

5.7 实战例子

1 从零开始码出卡尔曼滤波代码-BY忠厚老实的老王

2

六扩展卡尔曼滤波

七无痕卡尔曼滤波

八粒子滤波

madgick的姿态估算分析

流形上的卡尔曼滤波

不变卡尔曼滤波

自动驾驶方面的滤波建议-by忠厚老实的老王

不要使用粒子滤波这些

图优化

非线性优化

#参考资料
[1] http://www.starlino.com/imu_guide.html
[2] https://www.geek-workshop.com/thread-1695-1-1.html
[3]四元数资料 https://blog.csdn.net/guanjianhe/article/details/95608801
[4] 贝叶斯滤波瑜卡尔曼视频教程-by忠厚老实的老王 https://space.bilibili.com/287989852?from=search&seid=14942905287202594616&spm_id_from=333.337.0.0
[5]你真的搞懂贝叶斯滤波了吗？ https://blog.csdn.net/wq1psa78/article/details/105849353
[6] 从概率到贝叶斯滤波 https://blog.csdn.net/u012494154/article/details/112517756
[7] 从贝叶斯滤波到扩展卡尔曼滤波 https://blog.csdn.net/u012494154/article/details/112518871
[8] 从贝叶斯滤波到无迹卡尔曼滤波 https://blog.csdn.net/u012494154/article/details/112520830
[9] 从贝叶斯滤波到粒子滤波 https://blog.csdn.net/u012494154/article/details/120175011

Feisy

关注

5
点赞
踩
22

收藏

觉得还不错? 一键收藏
0
评论
使用IMU进行状态估计及进阶

前言本文章将汇总我这么长时间来，使用IMU进行姿态估计的总结，所以会很多内容，并且不能够一次性完成。我会分成很多次，一步步介绍下去。目前的计划是，从零开始介绍姿态估算，然后进一步介绍姿态估算与滤波的关系，然后介绍各个我知道的进阶算法。本文将采用状态估计，而不是姿态估计。因为姿态估计的范围比较狭小，是状态估计中的一部分，后续可能会介绍状态估计中的位置，速度等估计。基本思想状态估计=计算公式+数据首先，我们需要知道的是，给你一些传感器的数据，我们怎么根据这些数据来计算得到姿态？这个就是计算公式的作
复制链接

扫一扫