这一章非常重要,内容有些多,是后续章节的基础
- 刚体的速度由
 表示(twist):3个角速度,3个角速度
表示(twist):3个角速度,3个角速度 - 刚体的受力由
 表示(wrench):3个力矩,3个力
表示(wrench):3个力矩,3个力 - free vector: 只有长度和方向的向量,例如线速度向量就是自由向量
- space frame{s}: 可以理解为基座上的坐标系,定系,也叫fixed frame
- boby frame{b}: 可以理解为末端执行器上的坐标系,动系
- 笛卡尔坐标系约定:

1 刚体的在空间中的运动

- 在{s}坐标系下表示{b} ,注意带有
\hat{}^符号的向量是单位向量- 位置
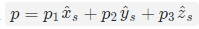
- 角度
- 位置

- 刚体在运动过程中无非就是平移+旋转,这个特别像螺旋运动(旋转+平移)
- 旋转轴:

- 旋转+平移表示为
 :绕旋转轴
:绕旋转轴 旋转
旋转
- 角速度+线速度表示为
 (可以理解为旋转+平移的微分)
(可以理解为旋转+平移的微分)
- 旋转轴:
2 旋转和角速度
2.1 旋转矩阵
2.1.1 旋转矩阵的性质
- 旋转矩阵R的性质:
- 由3列组成,每列3个元素
- 每列都是单位向量
- 任意两列之间互相垂直
- 通过线性代数的知识就可以知道,满足上面这三点的矩阵是3维的标准正交阵

- 群的概念
- 不要感觉它很高大上
- 只要满足以下四个性质,都可以称之为群,对于A,B属于一个集合(如:A,B属于标准正交阵的集合)
- 封闭性:AB还在这个集合中,(两个标准正交阵的乘积还是标准正交阵)
- 结合律:
 (矩阵乘法满足这个规律)
(矩阵乘法满足这个规律) - 存在单位元:
 (对于标准正交阵集合,单位矩阵就是单位元)
(对于标准正交阵集合,单位矩阵就是单位元) - 存在逆元:
 (对于标准正交阵集合,矩阵的转置就是矩阵的逆)
(对于标准正交阵集合,矩阵的转置就是矩阵的逆)
- 有了旋转矩阵的性质和群的概念,可以很清楚的知道,旋转矩阵的集合就是一个群,我们称之为特殊正交群,缩写SO(3)
2.1.2 旋转矩阵的使用
- 表示方向
 :坐标系{b}在坐标系{s}中的表示
:坐标系{b}在坐标系{s}中的表示
- 改变参考坐标系

- 在下一章求正运动学中会用到
- 旋转矢量或坐标系
- 将坐标系{s}绕转轴
 旋转
旋转 得到{s'}
得到{s'}
- 将坐标系{s}绕转轴
- 绕坐标轴的旋转公式:

- 更一般的旋转公式

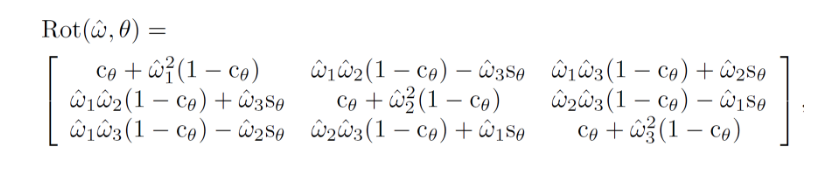
2.2 角速度
- 斜对称矩阵:斜对称矩阵被称为so(3)(李代数),给定向量
 ,则斜对称矩阵定义为:
,则斜对称矩阵定义为:

-
斜对称矩阵的应用
- 对于任意

,R∈SO(3),总有 成立
成立 - 将叉乘转化为点乘:
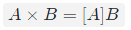
- 对于任意
- 求
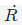 :
:
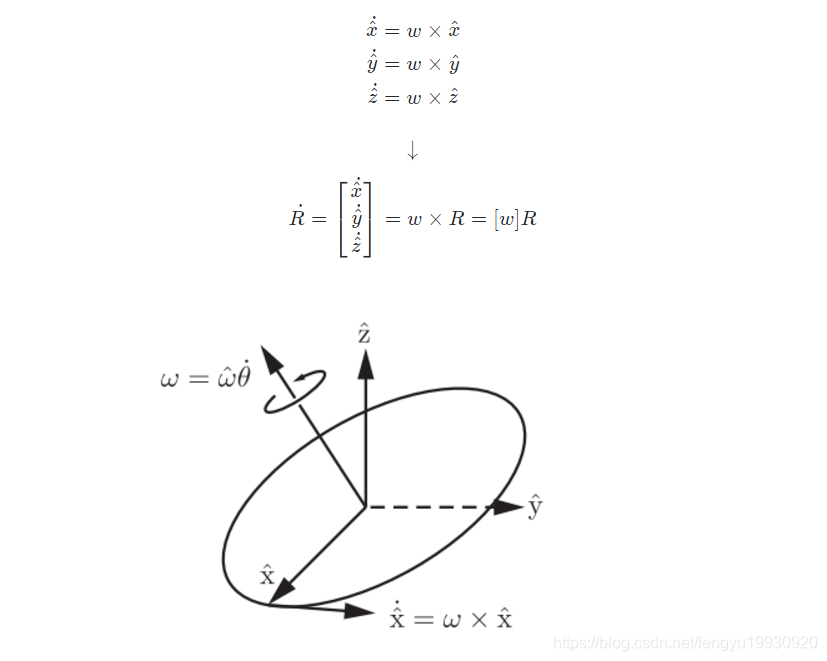
- 对于定坐标系{s}:

- 对于动坐标系{b}:

2.3 旋转的指数坐标表示
2.3.1 线性微分方程的求解
- 微分方程


- 将上式微分方程中的a转换为矩阵A时
 :
:

- 矩阵的指数方程满足下面性质:

- 如果矩阵A可以表示为
 (证明过程看书)
(证明过程看书) -
如果
 ,则
,则
-

2.3.2 旋转的指数坐标表示

- 已知
 时,位置在
时,位置在 ,绕着轴
,绕着轴 旋转,当
旋转,当 时,位置在
时,位置在 ,任意时刻线速度为:
,任意时刻线速度为:

- 旋转矩阵的指数表示如何计算:

- 旋转矩阵的指数表示为:

2.3.3 旋转的对数矩阵
- 旋转矩阵的指数表示为
 ,它的逆运算被称为对数矩阵
,它的逆运算被称为对数矩阵
- 已知
R,求 的计算过程:(推导过程见教材)
的计算过程:(推导过程见教材)
- 如果
 ,则
,则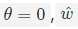 不能决定
不能决定 - 如果
 ,则
,则 为下面3个中有意义的一个:
为下面3个中有意义的一个:
- 如果

- 其他情况为:

3 刚体的运动与扭转
3.1 齐次变换矩阵
- 齐次变换矩阵:这个名词不要把它看得特别奇特,就是我们常说的
T,由旋转矩阵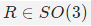 和位置向量
和位置向量 组成
组成 - 特殊欧拉群(Special Euclidean Group):前面说过,只要满足封闭性、结合律、存在单位元、存在零元都可以成为群,这里将具有齐次变换矩阵形式的矩阵集合称为特殊欧拉群


3.1.1 齐次变换矩阵的性质
- 齐次变换矩阵的逆还是齐次变换矩阵,而且求逆有简单方法

齐次变换矩阵的乘积还是齐次变换矩阵
满足结合律:
齐次坐标:已知坐标
,齐次坐标为
标准欧几里得范数: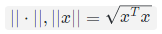

- 标准欧几里得內积

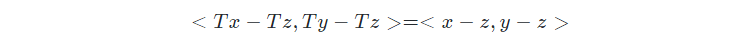
3.1.2 齐次变换矩阵的使用
- 主要用途:
- 刚体的位置和方向表示:

- 改变参考坐标系:

- 置换(旋转和平移)一个向量或坐标系:
- 刚体的位置和方向表示:

- 坐标变换(相对于固定坐标系{s}):

- 坐标变换(相对于动坐标系{b}):

3.2 Twists
3.2.1 Twists的理解
- 定义:
 ,b:代表{b}(body); s:代表{s}(space)
,b:代表{b}(body); s:代表{s}(space) - 斜对称矩阵:(推导过程看书)
 :在{b}坐标系下的角速度
:在{b}坐标系下的角速度
:在{s}坐标系下的角速度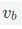 :在{b}坐标系下的线速度
:在{b}坐标系下的线速度 :在{s}坐标系下的线速度
:在{s}坐标系下的线速度

- 伴随矩阵:
 ,求
,求T的伴随矩阵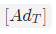

- T的伴随映射(T用于位置的变换,T的伴随用于速度的变换):

- 伴随矩阵的性质:

3.2.2 Twists的旋量解释
- 角速度
 可以表示为
可以表示为 ,
, 为单位向量,只表示方向
为单位向量,只表示方向 - twists也可以有类似的表示:
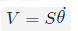
- 螺旋轴在这里也称为旋量
 ,可以由三个参数表示
,可以由三个参数表示
 : 螺旋轴上的任意一点
: 螺旋轴上的任意一点 : 螺旋轴方向上的单位向量
: 螺旋轴方向上的单位向量 : 螺距,绕轴线转动一圈而沿轴线移动的距离(线速度/角速度
: 螺距,绕轴线转动一圈而沿轴线移动的距离(线速度/角速度
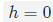 :纯选择
:纯选择 :纯移动
:纯移动


3.3 刚体运动的指数坐标表示

3.3.1 刚体运行的指数表示

3.3.2 刚体运行的对数表示

4 Wrenches
- 上一节主要讲的是运动学有关的物理量在指数空间上的表示,这一节讲解动力学有关的物理量在指数空间上的表示
- 定义一个6维空间力在坐标系
{a}中的表示,也叫wrench,符号为
(实际上就是力矩和力的结合)
- 功率与坐标系的选择无关:

- 固定坐标系{s}与末端执行器动坐标系{b}之间的转换

5 总结
- 最后给出总结:(摘自 (美)John J. Craig写的《Introduction to Robotics Mechanics and Control》)













 本文详细介绍了刚体在空间中的运动,包括旋转矩阵的性质和使用、角速度、旋转的指数坐标表示以及刚体运动与扭转。重点讨论了旋转矩阵的群概念、齐次变换矩阵及其在机器人运动学中的应用。
本文详细介绍了刚体在空间中的运动,包括旋转矩阵的性质和使用、角速度、旋转的指数坐标表示以及刚体运动与扭转。重点讨论了旋转矩阵的群概念、齐次变换矩阵及其在机器人运动学中的应用。

















 1386
1386

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








