学习笔记之——VIO与VINS-Mono

为什么需要IMU呢？是因为在纯视觉的slam或者vo中，由于图像的运动模糊、遮挡、快速运动、纯旋转、尺度不确定性的一系列问题，导致仅靠一个摄像头很难完成我们实际场景的应用需求，而IMU直接可以得到运动主体自身的角速度、加速度的测量数据，从而对运动有一个约束，或者说与视觉形成互补，可实现快速运动的定位和主体纯旋转的处理，从而进一步提高slam/vio的可靠性。

首先对VIO有个基本的了解，再看VINS-Mono会容易理解一些~~~本部分主要参考了深蓝学院的《从零开始手写vio 视觉slam进阶》

IMU 测量模型与运动模型

IMU(Inertial Measurement Unit)
惯性测量单元
典型 6 轴 IMU 以较高频率(≥100Hz)返回被测量物体的角速度与加速度
受自身温度、零偏、振动等因素干扰,积分得到的平移和旋转容易漂移
六自由度 IMU 本身由一个陀螺仪和一个加速度计组成,分别测量自身的角速度和加速度。

旋转坐标系下的运动学

线速度与角速度的关系如下所示：

如下所示，inertial frame就是我们所说的惯性系，也就是世界坐标系；body frame可以看作就是imu系

下面公式，先忽略平移变换

分布求导

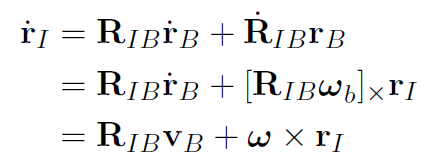
文字表达就是：惯性系下的速度=body系的速度*body到惯性系的转换+惯性系上body的角速度*object在惯性坐标系的位置。

下面用到了李代数，因为旋转矩阵求导，其实就是李群李代数方面的知识了《学习笔记之——李群与李代数的理解》

body系下的加速度并不直接等于世界坐标系下的加速度

IMU 测量模型

MEMS 加速度计工作原理

测量原理可以用一个简单的质量块+ 弹簧+ 指示计来表示
加速度计测量值am 为弹簧拉力对应的加速度，而不是直接读取body的加速度

测量原理可以用一个简单的质量块+ 弹簧+ 指示计来表示

加速度计测量值am 为弹簧拉力对应的加速度，
MEMS 加速度计利用电容或者电阻桥来等原理来测量am，如下图所示

加速度计测量原理

东北天坐标系（ENU）

假设IMU 坐标系就是ENU 坐标系， $R_{IB}=I$ ，静止时有（am为测量值，a为body系的加速度值）

注意这里的“-”号是不同厂商可能有不同的定义

自由落体时有（注意 $a_{m}$ 为加速度计的测量值）：

陀螺仪测量原理

陀螺仪主要用来测量物体的旋转角速度，按测量原理分有振动陀螺，光纤陀螺等。
低端MEMS 陀螺上一般采用振动陀螺原理，通过测量Coriolis force （科氏力）来间接得到角速度。
在旋转坐标系中，运动的物体受到科氏力作用
MEMS 陀螺仪：一个主动运动轴 + 一个敏感轴

音叉振动陀螺（如下图所示），叉子的中间为旋转轴，叉子左右两个质量块，做方向相反的正弦运动，质量块受到的科氏力方向相反。

陀螺仪的G-sensitivity

实际上，两个质量块不可能完全一致，也就是说陀螺仪的测量可能会受到外部加速度的影响，即常称的G-sensitivity。

由于陀螺仪在测量的时候，本身会高速运动，所以有科氏力的影响，但是加速度计则不会，因为起测量的时候，没有在某个轴上高速运动

IMU 误差模型

误差分类

加速度计和陀螺仪的误差可以分为：确定性误差，随机误差。

随机误差通常假设噪声服从高斯分布，包括：高斯白噪声，bias随机游走...

哪怕标定比较准确，但实际上还是有点差别的，所以把早上作为状态的一个量，一起来估计？

高斯白噪声

实际上，IMU 传感器获取的数据为离散采样，离散和连续高斯白噪声的方差之间存在如下转换关系：

即

其中，

也就是说高斯白噪声的连续时间到离散时间之间差一个，其中是传感器的采样时间

Bias 随机游走——通常用维纳过程(wiener process) 来建模bias 随时间连续变化的过程，离散时间下称之为随机游走

其中w 是方差为1 的白噪声

随机误差其实也有标定的方法。这里就不具体描述了哈~个人觉得有点类似把均值和方差求出来，得到随机噪声模型~

确定性误差可以事先标定确定，包括：bias, scale ...

Bias是指——理论上，当没有外部作用时（静止的时候），IMU 传感器的输出应该为0（对于陀螺仪为0，对于加速度计应该是-g，但是读数为-g实际也可以转到0）。但是，实际数据存在一个偏置b。加速度计bias 对位姿估计的影响为：

scale则是指—— 可以看成是实际数值和传感器输出值之间的比值。

换言之就是实际的值跟输出的值的关系为：

measured=scale*true+bias

Nonorthogonality/Misalignment Errors（非正交误差，其他轴在其上有影响）——多轴IMU 传感器制作的时候，由于制作工艺的问题，会使得xyz 轴可能不垂直，如下图所示。

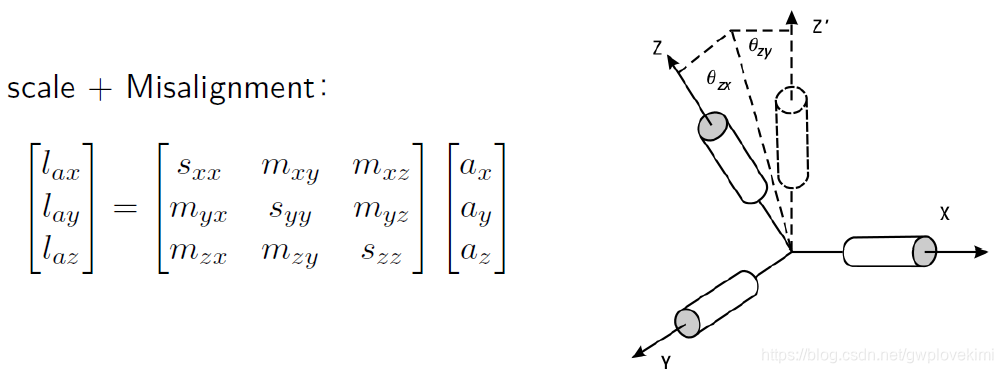
除此以外，bias在不同上电期间，上电后的不同时长，可能都有不同的bias；当然还有温度影响（温度补偿）

上面的就是确定误差，可以进行标定的。下面会讲大概的标定的方法

确定误差的标定

六面法标定加速度bias 和scale factor

六面法是指将加速度计的3 个轴分别朝上或者朝下水平放置一段时间，采集6 个面的数据完成标定。如果各个轴都是正交的，那很容易得到bias 和scale：

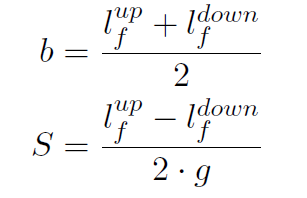
其中，l 为加速度计某个轴的测量值，g 为当地的重力加速度。

当考虑轴间误差的时候，实际加速度和测量值之间的关系为：

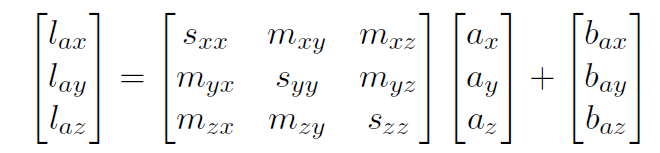
水平静止放置6 面的时候，加速度的理论值为：

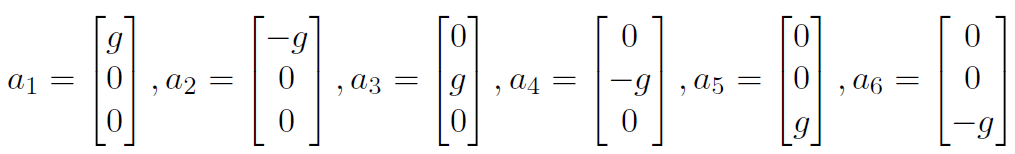
对应的测量值矩阵L ：

利用最小二乘就能够把12 个变量求出来。

六面法标定陀螺仪bias 和scale factor

和加速度计六面法不同的是，陀螺仪的真实值由高精度转台提供（通过以想要的角速度进行旋转），这里的6 面是指各个轴顺时针和逆时针旋转。

温度相关的参数标定

目的：这个标定的主要目的是对传感器估计的bias 和scale 进行温度补偿，获取不同温度时bias 和scale 的值，绘制成曲线。有两种标定方法：

soak method: 控制恒温室的温度值，然后读取传感器数值进行标定。
ramp method：记录一段时间内线性升温和降温时传感器的数据来进行标定。

加速度计的误差模型

导航系G 为东北天坐标系（ENU）；理论测量值为：

如果考虑高斯白噪声，bias，以及尺度因子，则为：

通常假设尺度因子为单位矩阵。

陀螺仪的误差模型

考虑尺度因子，高斯白噪声，以及bias, 陀螺仪的误差模型如下：

低端传感器，考虑加速度对陀螺仪的影响，即g-灵敏度：

陀螺仪受四种噪声的影响分别如下图所示：

VIO 中的IMU运动模型

忽略scale 的影响，只考虑白噪声和bias 随机游走：

上标g 表示重力，a 表示加速度，w 表示在世界坐标系world，b 表示body frame （IMU frame）；等号左边的为测量值，右边的对应的w和a为真实值。P(ose),V(elocity),Q(uaternion) 对时间的导数可写成：

q要做归一化，成为单位四元数

连续时间下IMU 运动模型

根据上面的导数关系，可以从第i 时刻的PVQ，通过对IMU 的测量值进行积分，得到第j 时刻的PVQ（这就是下文会提到的，IMU的预积分）:

运动模型的离散积分——欧拉法

使用欧拉法，即两个相邻时刻k 到k+1 的位姿是用第k 时刻的测量值a,w来计算（认为这个时间段的加速度与角速度不变）。

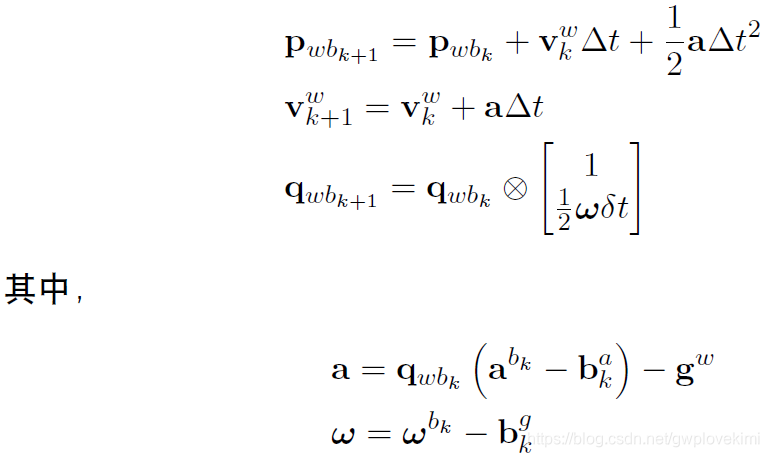
运动模型的离散积分——中值法

使用mid-point 方法，即两个相邻时刻k 到k+1 的位姿是用两个时刻的测量值a,w的平均值来计算。

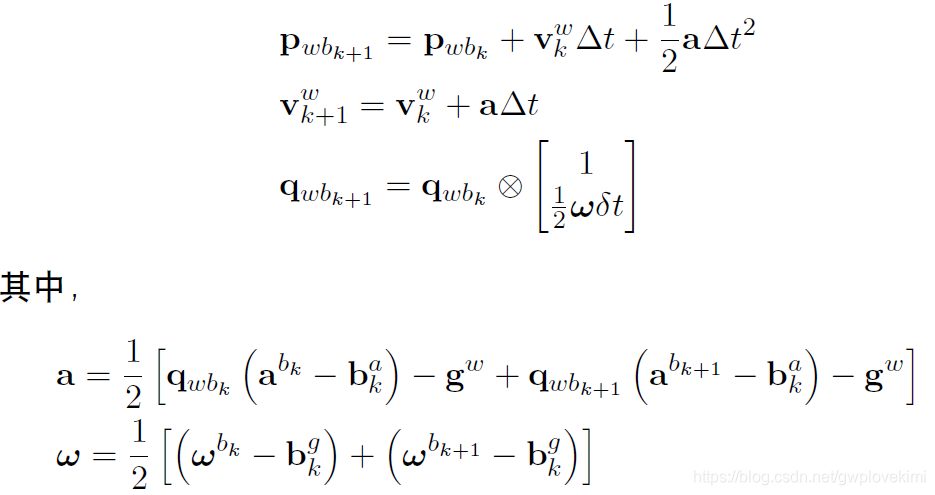
基于优化的IMU预积分与视觉信息融合

这是基于优化的框架的（当然还有基于滤波的）

基于Bundle Adjustment 的VIO 融合

Bundle Adjustment(BA)中文有多种翻译法：光束法平叉、束调整、捆集调整、捆绑调整等。BA的本质是一个优化模型，其目的是最小化重投影误差。什么是重投影误差呢？

重投影误差

如下图所示，空间物体通过相机在图像平面所成像就称之为投影。下图中红色的qij特征点就是空间三维立方体（不是图上方的那个立方体，图中未画出）在图像平面的投影。然后我们利用前面所述的运动估计方法可以估计qij对应的可能的三维空间点位置（Xj点，不一定是真实的位置）。然后我们利用估计的三维空间点Xj和计算的相机参数Ci（不一定是真值）重新进行投影，此时投影到图像中的位置为P(Ci,Xj)，由于估计位姿和相机参数时存在一定的误差，所以重投影点P(Ci,Xj)和第一次的投影qij有一定的偏差，就称为重投影误差。目标函数就是最小化这个重投影误差。

而通常使用的是窗口BA，它将当前图像和之前的n-1幅图像帧作为一个窗口进行优化，这样不仅可以跟踪前一个相机位姿还可以跟踪更之前的相机位姿，保证当前和前n-1个相机位姿一致。因此，窗口BA可以减小漂移。窗口大小n的选择决定了计算复杂度，选择较小的窗口数量可以限制优化的参数的数量，使得实时BA成为可能。

BA

从视觉重建中提炼出最优的3D模型和相机参数（内参和外参）。从每一个特征点反射出来的几束光线，在我们把相机姿态与特征点的空间位置做出最优调整（adjustment）之后，最后收束到相机光心的过程称为BA

视觉SLAM 里的Bundle Adjustment 问题

BA指的是下面的优化问题：相机在不同的pose下看到了一些目标点。当给定三维特征点初始的三维位置跟相机的pose以及观测的测量值后，如何优化这些测量值

已知：

状态量初始值：特征点的三维坐标，相机的位姿。
系统测量值：特征点在不同图像上的图像坐标。

问题：如何估计状态量的最优值？解决方法就是：构建误差函数，利用最小二乘得到状态量的最优估计（计算最优的重投影误差）

上面的那个范数是用于调节误差的权重的。关于BA优化问题，在代码仲一般可通过g2o or ceres来求解。基于LM算法来求解。对于BA具体的求解过程，目前还不是特别清晰，后续继续深入看看

VIO 信息融合问题

视觉SLAM中的BA问题可以看作下图所示

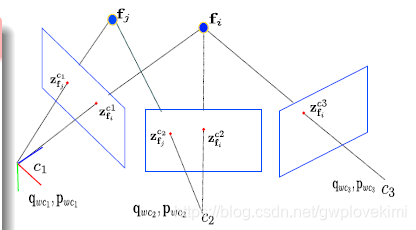
而VIO中，则多出了IMU的约束，如下图所示。两个图像间，有很多的IMU数据，因此需要把这些IMU数据做一个预积分，这样使得起变成只有一个约束

其中，就引入了IMU的误差，进而引出下面的问题

那么最基本的解决这个优化问题，可以采用最小二乘法。

在介绍最小二乘法之前，先看看IMU的预积分

IMU的预积分

由于imu的数据采集频率大于相机的采集频率，所以在两个相机坐标系之间，存在多个imu坐标系（body坐标系），由于相机坐标系应跟body坐标系相对应，所以对两图像间的imu数据进行预积分，使其变为一个。

在视觉slam系统中为了减小优化求解器的负担，采用了关键帧策略，而IMU的速率显然要快于关键帧的插入，它们之间的关系可以用下图很好的表示。

紧耦合的方式就是通过imu和图像的信息共同来估计状态量，所以如何协调两者之间的关系就是通过IMU的预积分来做的了。通过重新参数化，把关键帧之间的IMU测量值积分成相对运动的约束，避免了因为初始条件变化造成的重复积分。

在bundle adjustment里，参与对象是keyframe，比如有2个keyframe：他们的位姿分别为：那么他们的相对位姿 :

我们可以认为 $P_{21}$ 为估计项，是由SLAM的位姿直接算出来的。如果要构成一个优化问题，我们还需要知道误差项和测量项。没错，是IMU可以计算在这两个KF间的测量项 $P_{imu}$ ，预计分干的事情就是计算这个测量项。

在紧耦合的优化slam中，IMU就是提供了两个关键帧的相对测量，从而构建误差函数对关键帧姿态的迭代优化。当然实际应用中不会是这么简单的形式，这里面要对各个变量分别求取误差，然后求雅克比矩阵。

从上面的IMU运动模型中，我们可以知道MU可以干的事情就是由上个时刻t状态可以推算出下个时刻的状态，这里的状态就是旋转角度、速度和位置（前面提到的PVQ）上面也给出了积分的形式了~

最小二乘问题的求解

关于非线性优化，可以参考之前的博客《学习笔记之——非线性优化的解读》

最小二乘基础概念

对损失函数进行泰勒展开（三阶项以上都忽略）：

一般采用迭代下降法来求解。关于非线性优化的求解问题，可以参考之前的博客《学习笔记之——非线性优化的解读》由于实际的过程一般通过函数求解，个人觉得。这部分理解即可。那么总结整个最小二乘求解的过程就是：

那么这里的第一个关键就是，关于状态量的残差函数。

VIO 残差函数的构建

基于滑动窗口的VIO Bundle Adjustment：

下面看看怎么得来的~

首先看看系统需要优化的状态量。为了节约计算量采用滑动窗口形式的Bundle Adjustment, 在i 时刻，滑动窗口内待优化的系统状态量定义如下:

λ是逆深度

视觉重投影误差

定义:一个特征点在归一化相机坐标系下的估计值（投影）与观测值的差。

其中，待估计的状态量为特征点的三维空间坐标，观测值为特征在相机归一化平面的坐标。

逆深度参数化

特征点在归一化相机坐标系与在相机坐标系下的坐标关系为：

其中 λ = 1 / z 称为逆深度(更接近于高斯分布)。
VIO 中基于逆深度的重投影误差

特征点逆深度在第 i 帧中初始化得到,在第 j 帧又被观测到,预测其在第 j 中的坐标为:

将i帧中观测到的数据变换到相机坐标系，将相机坐标系变换到body坐标系，将第i个body坐标系变换到世界坐标系，将世界坐标系变换到第j个body坐标系，将body坐标系变换到相机坐标系，得到第j帧的预测值。这期间相对于纯视觉多了相机坐标系变换到body坐标系，然后再由body坐标系变换回相机坐标系的过程。（注意，这其中的两个T是转置）

视觉重投影误差为:

IMU 测量值积分

从第i 时刻的PVQ 对IMU 的测量值进行积分得到第j 时刻的PVQ:

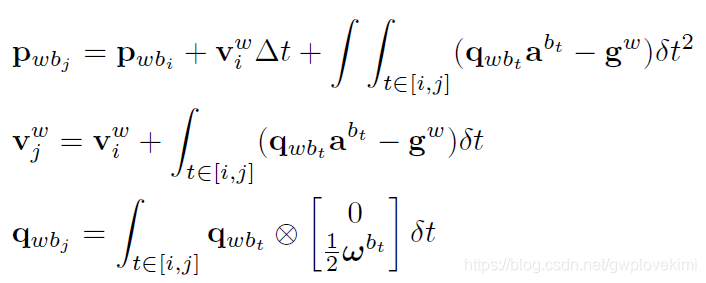
每次优化更新后，都需要重新进行积分，运算量较大。故此采用预积分解决方案（直观理解就是，只更新相对位置下的积分？否则每次变动就需要重新全部积分）

IMU 预积分

一个很简单的公式转换，就可以将积分模型转为预积分模型：

那么，PVQ 积分公式中的积分项则变成相对于第i 时刻的姿态，而不是相对于世界坐标系的姿态（注意，积分的是积从i到j的变化）：

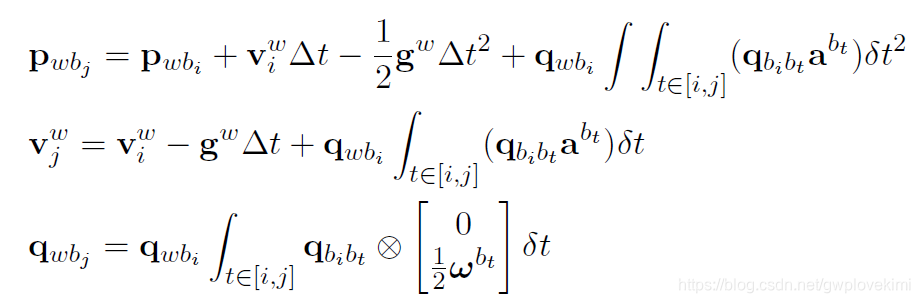
这里的预积分量仅仅跟IMU 测量值有关，它将一段时间内的IMU 数据直接积分起来就得到了预积分量：

重新整理下PVQ 的积分公式，有：

IMU 的预积分误差

预积分误差。定义：一段时间内IMU 构建的预积分量作为测量值，对两时刻之间的状态量进行约束

上面误差中位移,速度,偏置都是直接相减得到。第二项是关于四元数的旋转误差,其中 [·] xyz 表示只取四元数的虚部 (x, y, z) 组成的三维向量。

关于预积分的计算，前面提到过有欧拉法与中值法。这里使用mid-point 方法，即两个相邻时刻k 到k+1 的位姿是用两个时刻的测量值a,w 的平均值来计算：

预积分量的方差

一个IMU 数据作为测量值的噪声方差我们能够标定。现在，一段时间内多个IMU 数据积分形成的预积分量的方差呢？

要推导预积分量的协方差，我们需要知道imu 噪声和预积分量之间的线性递推关系。

协方差的传递

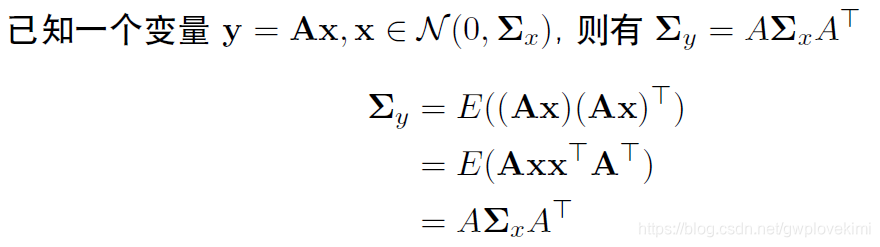
假设已知了相邻时刻误差的线性传递方程：

比如：状态量误差为，测量噪声为。误差的传递由两部分组成：当前时刻的误差传递给下一时刻，当前时刻测量噪声传递给下一时刻。协方差矩阵可以通过递推计算得到：

其中，是测量噪声的协方差矩阵，方差从i 时刻开始进行递推，

状态误差线性递推公式的推导如下

通常对于状态量之间的递推关系是非线性的方程如，其中状态量为x，u 为系统的输入量。

我们可以用两种方法来推导状态误差传递的线性递推关系：

一种是基于一阶泰勒展开的误差递推方程。
一种是基于误差随时间变化的递推方程。

基于一阶泰勒展开的误差递推方程（应用于EKF 的协方差预测）

令状态量为其中，真值为，误差为。另外，输入量u 的噪声为n。对于非线性系统（传递方程）的状态误差的线性递推关系如下：

基于误差随时间变化的递推方程

如果我们能够推导状态误差随时间变化的导数关系，比如：

则误差状态的传递方程为：

预积分的误差递推公式推导

首先回顾预积分的误差递推公式，将测量噪声也考虑进模型：

确定误差传递的状态量，噪声量，然后开始构建传递方程。

预积分误差传递的形式

用前面一阶泰勒展开的推导方式，我们希望能推导出如下的形式（误差的传递）：

F,G 为两个时刻间的协方差传递矩阵。这里我们直接给出F,G 的最终形式：

其中的系数为：

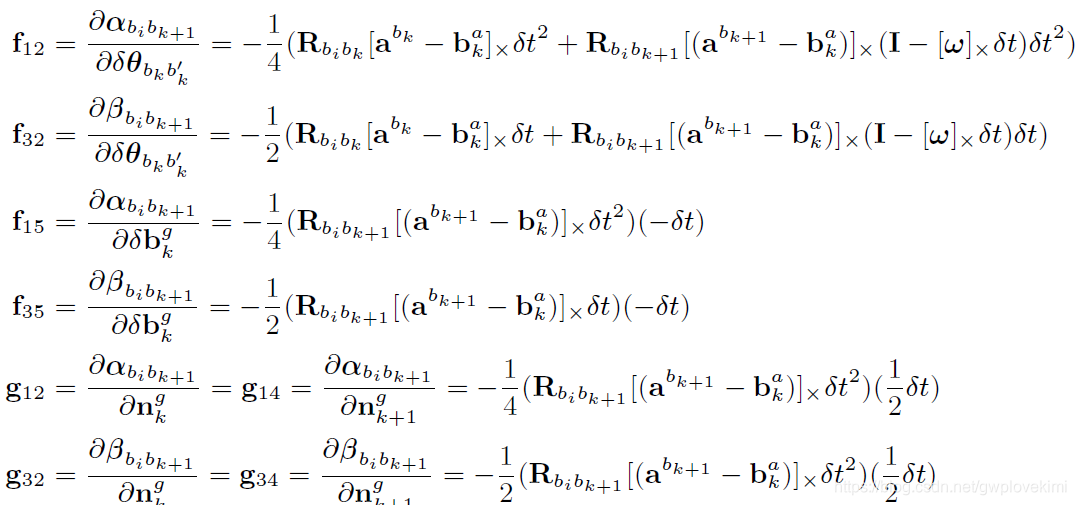
雅克比矩阵F,G 的推导

公式简化约定：考虑到公式的编辑篇幅，为了对一些求导公式进行简化，这里做一些简单的约定, 比如求导公式：

后续直接简写为

雅克比矩阵F 的推导

f32: 对角度预积分量的Jacobian

Part 1 对应的的雅克比为：

Part 2 对应的的雅克比为：

将上面两部分综合起来就能得到

f35: 速度预积分量对k 时刻角速度bias 的Jacobian。递推公式如下：

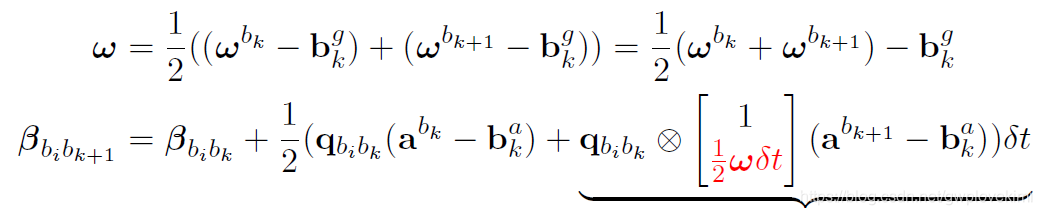
只有红色公式部分和角速度bias 有关系，因此雅克比的推导只考虑红色公式部分。

旋转预积分量的Jacobian，即F 第二行

旋转预积分的递推公式为：

下面开始详细推导：

注意：上面推导过程，也可以用李代数的右扰动。只考虑上式中的虚部：

那么，第k+1 时刻的旋转预积分的误差相对于第k 时刻的Jacobian为：

获得残差函数后，我们需要得到其雅克比矩阵（J）

残差Jacobian 的推导

视觉重投影残差的Jacobian

视觉残差为：

对于第i 帧中的特征点，它投影到第j 帧相机坐标系下的值为：

拆成三维坐标形式为：

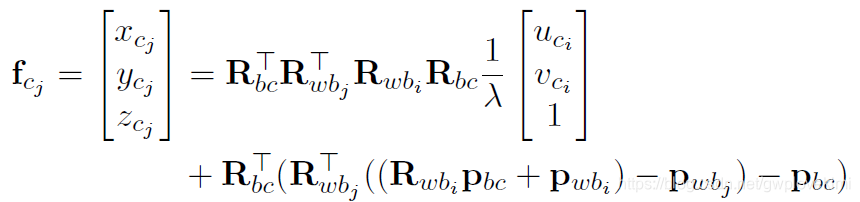
再推导各类Jacobian 之前，为了简化公式，先定义如下变量：

Jacobian 为视觉误差对两个时刻的状态量，外参，以及逆深度求导：

上面公式和i 时刻角度相关的量并不多，下面为了简化，直接丢弃了不相关的部分

Jacobian 为

2. 对j 时刻的状态量求导
a. 对位移求导：

b. 对角度增量求导，同上面的操作，也简化一下公式

Jacobian 为

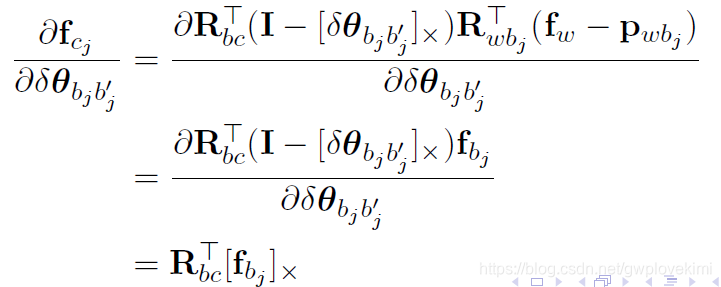
3. 对imu 和相机之间的外参求导

那么，第一部分的Jacobian 为：

第二部分的Jacobian 为：

两个Jacobian 相加就是视觉误差对外参中的角度增量的最终结果。

3. 视觉误差对特征逆深度的求导

IMU 误差相对于优化变量的Jacobian

上式可写为：

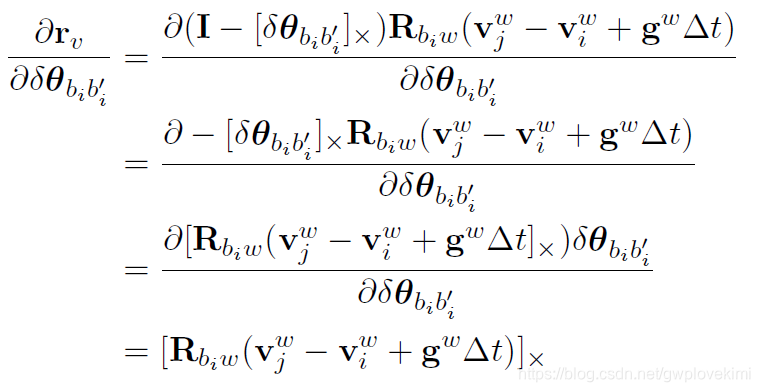
IMU 角度误差相对优化变量的Jacobian

(1) 对i 时刻姿态求导

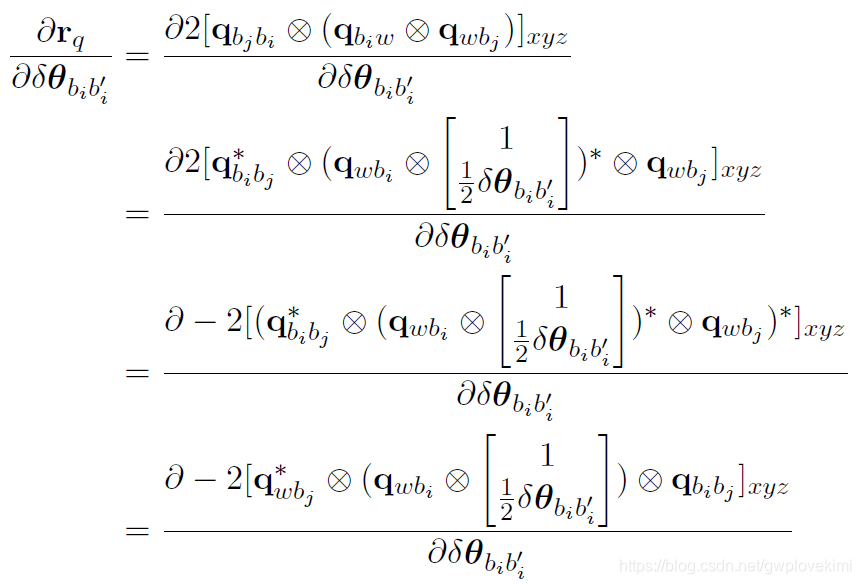
上式可化简为：

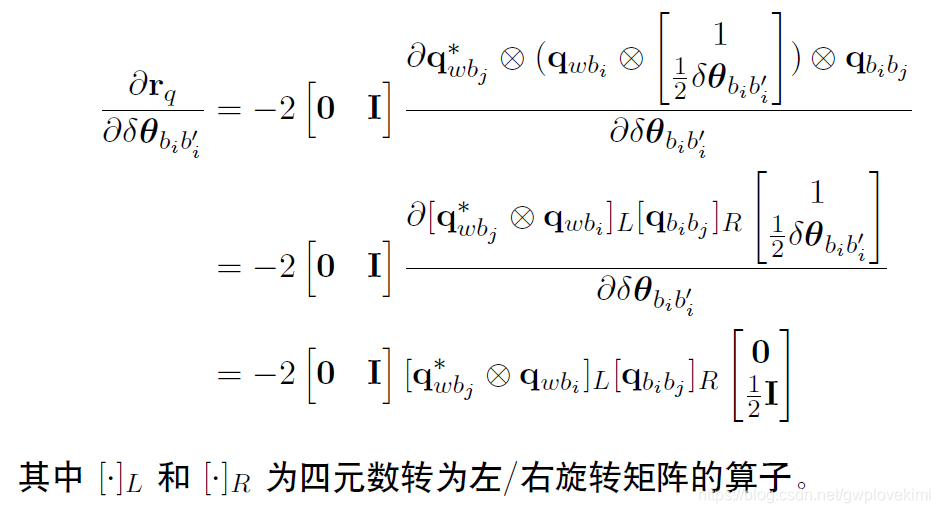
(2) 角度误差对j 时刻姿态求导

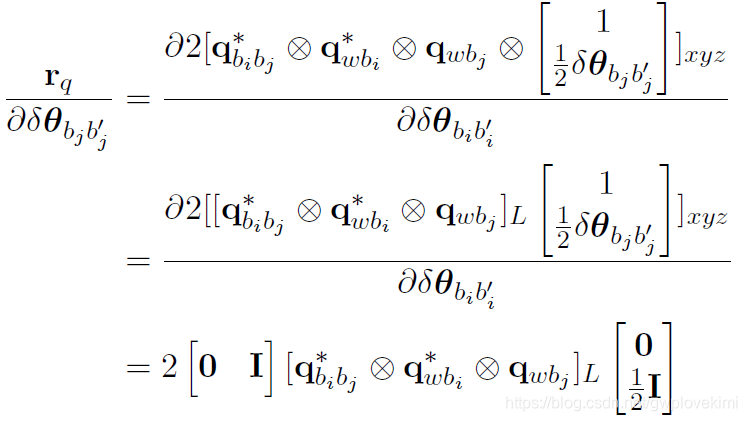
天呐。。。这堆公式真的。。。。。。

基于滑动窗口算法的VIO 系统：可观性和一致性

从高斯分布到信息矩阵

SLAM问题的建模

SLAM 问题求解

后验公式(2) 中分母跟状态量无关，舍弃。最大后验变成了：

即（负号变成min，加log从连乘变成加号）

如果假设观测值服从多元高斯分布：

则有：

这个最小二乘的求解可以使用之前的基于优化的解法：

上面的方差矩阵，其实相当于权重？？？

高斯分布和协方差矩阵

多元高斯分布

零均值的多元高斯分布有如下概率形式：

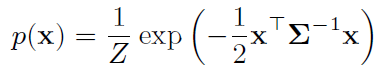
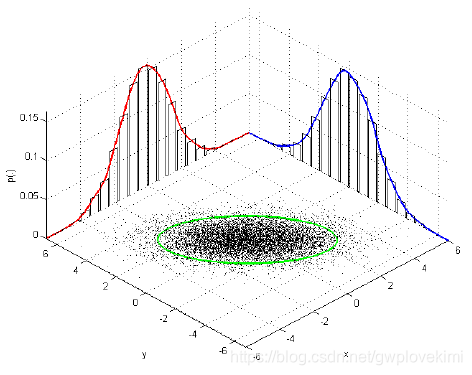
当维数变大时，求解计算量巨大。如何优雅的从多元高斯分布中丢弃变量？

通过信息矩阵（协方差矩阵的逆）来进行处理。具体例子分析可以参考：https://blog.csdn.net/qq_41990294/article/details/105232935

协方差矩阵对角线上的某个元素为0，即证明该位置对应的两元素相互独立，但是却不意味着其信息矩阵对应位置上的元素为0.

从多元高斯分布中，去掉一些变量后，其协方差矩阵与信息矩阵的变化：协方差矩阵是简单的去掉某个项，只剩余剩下的量的协方差。但信息矩阵却不是。如下所示

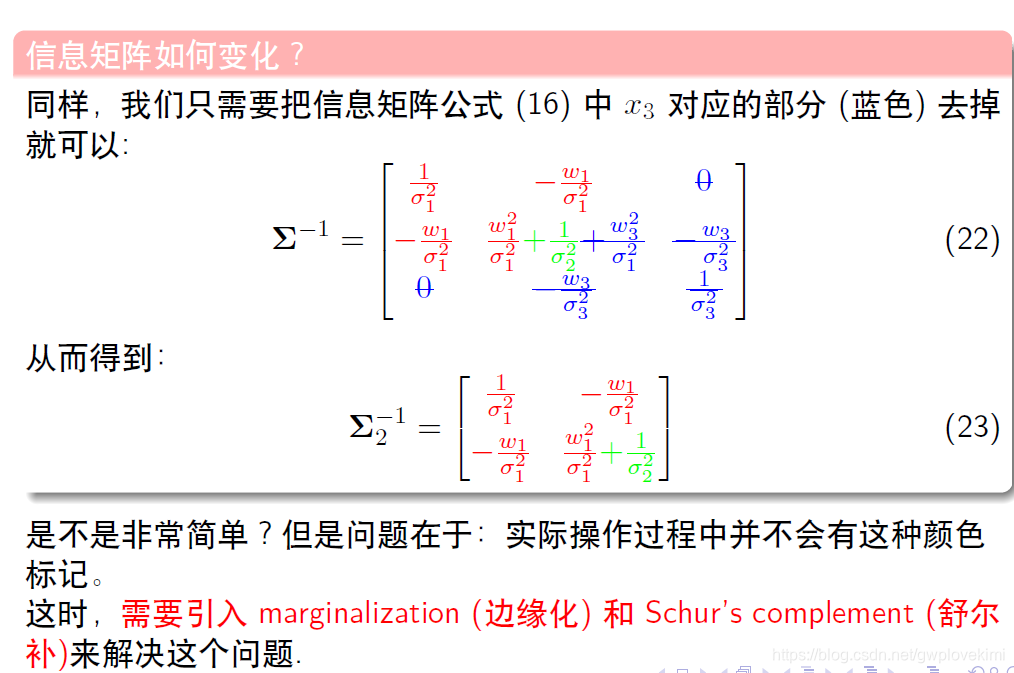
接下来看看如何通过信息矩阵来处理要移除的项——通过舒尔补（因为对于滑动窗口法而言，随着时间的变化，有一些新的量要加入，旧的量要移除，本来是一个联合分布，丢掉一部分信息后，协方差矩阵、信息矩阵如何变化~ ）

舒尔补应用：边际概率, 条件概率

舒尔补定义——给定任意的矩阵块M，如下所示:

滑动窗口算法

有如下最小二乘系统，对应的图模型如下图所示：

其中（6个变量，5个残差）

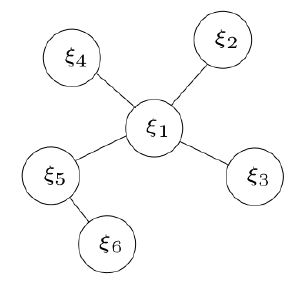
图优化~

圆圈：表示顶点，需要优化估计的变量.
边：表示顶点之间构建的残差。有一元边（只连一个顶点），二元边，多元边...

上述最小二乘问题，对应的高斯牛顿求解为：

雅克比矩阵，信息矩阵的稀疏性

由于每个残差只和某几个状态量有关，因此，雅克比矩阵求导时，无关项的雅克比为0。比如

信息矩阵组装过程的可视化。将五个残差的信息矩阵加起来，得到样例最终的信息矩阵, 可视化如下（下面的方块为：状态1~6，有颜色的为相关）：

当状态之间的边不是太多时，如上图所示，该矩阵还是比较稀疏的

基于边际概率的滑动窗口算法

为什么SLAM 需要滑动窗口算法?

随着VSLAM 系统不断往新环境探索，就会有新的相机姿态以及看到新的环境特征，最小二乘残差就会越来越多，信息矩阵越来越大，计算量将不断增加。
为了保持优化变量的个数在一定范围内，需要使用滑动窗口算法动态增加或移除优化变量。

滑动窗口算法大致流程

增加新的变量进入最小二乘系统优化
如果变量数目达到了一定的维度，则移除老的变量。
SLAM 系统不断循环前面两步

疑问：怎么移除老的变量？直接丢弃这些变量吗？

利用边际概率移除老的变量

直接丢弃变量和对应的测量值，会损失信息。正确的做法是使用边际概率，将丢弃变量所携带的信息传递给剩余变量。

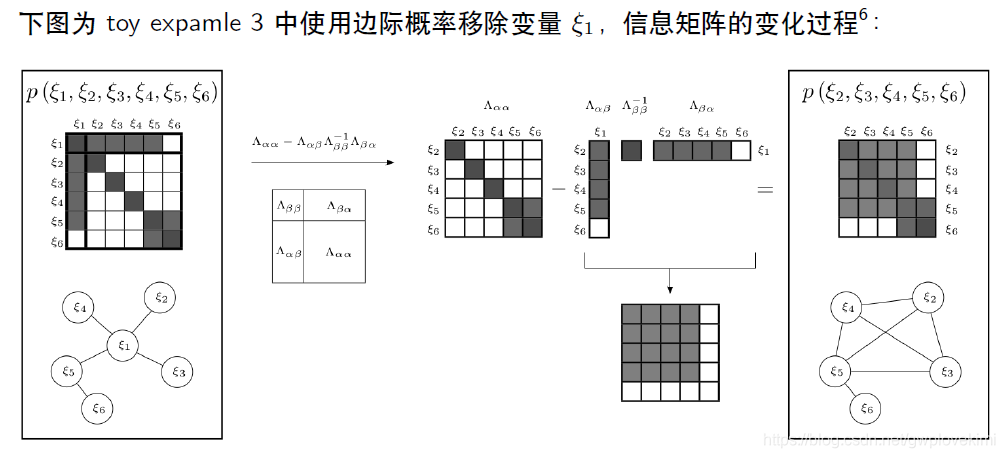
思考：如果是直接丢弃，信息矩阵如何变化？用边际概率来操作又会带来什么问题？

marginalization 会使得信息矩阵变稠密！原先条件独立的变量，可能变得相关。

滑动窗口中的FEJ （First Estimated Jacobian）算法

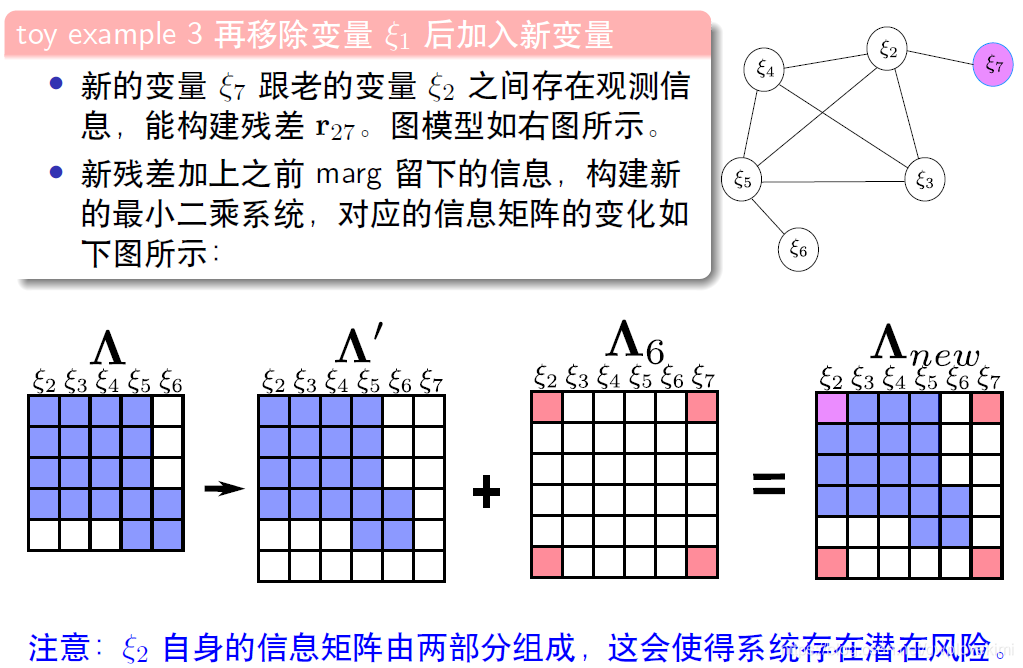
加入新的变量后，信息矩阵的变化~

滑动窗口算法

最小二乘问题的求解

直接求解计算量太大了~故此采用舒尔补来求解~通过求边际概率来把问题的规模缩小。

下面举一个单目相机的例子。对应不同的相机pose与特征点，假如每个相机pose有几十个特征点，那么对应的信息矩阵会特别的庞大。但其实其是稀疏的。通过舒尔补，边际概率把问题的规模减少。

VINS-Mono 中的滑动窗口算法

一些基础知识的补充

四元数的左乘右乘以及导数定理（左扰动与右扰动）

VINS-Mono概述

原文：VINS-Mono A Robust and Versatile Monocular Visual-Inertial State Estimator

VINS-Mono算是下面三篇论文的结合与加强版本，所以个人认为，在读其之前，先读一下下面三篇论文

[6] T. Qin and S. Shen, “Robust initialization of monocular visual-inertial estimation on aerial robots,” in Proc. IEEE/RSJ Int. Conf. Intell. Robots Syst., Vancouver, Canada, 2017, pp. 4225–4232.
[7] P. Li, T. Qin, B. Hu, F. Zhu, and S. Shen, “Monocular visual-inertial state estimation for mobile augmented reality,” in Proc. IEEE Int. Symp. Mixed Augmented Reality, Nantes, France, 2017, pp. 11–21.
[8] T. Qin, P. Li, and S. Shen, “Relocalization, global optimization and map merging for monocular visual-inertial SLAM,” in Proc. IEEE Int. Conf. Robot. Autom., Brisbane, Australia, 2018.

VINS-Mono的前身版本

Robust initialization of monocular visual-inertial estimation on aerial robots

Monocular visual-inertial state estimation for mobile augmented reality

Relocalization, global optimization and map merging for monocular visual-inertial SLAM

long-term drift is unavoidable for visual-inertial odometry (VIO). In order to eliminate the drift, loop detection, relocalization, and global optimization has to be developed.

VINS-Mono是港科大学开源的一个VIO算法，通过紧耦合方法实现的，通过单目+IMU恢复出尺度，效果非常棒。VINS是一种具有鲁棒性和通用性的单目视觉惯性状态估计器。该算法主要有以下几个模块：

数据预处理
图像特征光流跟踪
IMU数据预积分
初始化
纯视觉Sfm
Sfm与IMU积分的松耦合
基于滑动窗口的非线性优化实现紧耦合（后端非线性优化）
回环检测与重定位（闭环检测）
四自由度位姿图优化（闭环优化）

其架构如下图所示。第一部分是Measuremen Preprocessing：传感器观测值数据预处理，包含图像数据跟踪（基于光流）以及IMU数据预积分；第二部分是Initialization：初始化，包含单纯的视觉初始化（sfm）和视觉惯性联合初始化（松耦合）；第三部分Local Visual-Inertia BA and Relocalization：局部BA联合优化和重定位，包含一个基于滑动窗口的BA优化模型；第四部分Global Pose Graph Optimization：全局图优化，只对全局的位姿进行优化；第五部分Loop detection：回环检测。

代码中主要开启了四个线程，分别是：

1）前端图像跟踪

2）后端非线性优化（其中初始化和 IMU 预积分在这个线程中）

3）闭环检测

4）闭环优化。

各个功能模块主要有如下作用：

图像和 IMU 预处理

图像：提取图像 Harris 角点，利用金字塔光流跟踪相邻帧，通过 RANSAC 去除异常点，最后将跟踪到的特征点 push 到图像队列中，并通知后端进行处理。

IMU：将 IMU 数据进行积分，得到当前时刻的位置、速度和旋转（PVQ），同时计算在后端优化中将用到的相邻帧的预积分增量，及预积分误差的 Jacobian 矩阵和协方差项。

IMU预积分（Pre-integration ）

直观理解应该是对于IMU而言，其采样频率特别的高，对相邻一定时间的IMU进行积分，得到下图的转换效果。

IMU预积分的作用是计算出IMU数据的观测值（就是IMU预积分值）以及残差的协方差矩阵和雅各比矩阵。

在视觉中，这三个量也是非常重要的。其中，视觉中观测值是用来计算残差的（也就是误差），残差的雅各比矩阵是优化中下降的方向（也就是梯度），而协方差矩阵其实是观测值对应的权值。

故此，通过IMU预积分算出来的这三个量是为后面的联合初始化提供初值以及后端优化提供IMU的约束关系。

原始陀螺仪和加速度计的观测值数据：

第一个式子等式左边是加速度测量值（可以从加速度计中读到的值），等式右边是加速度真实值（其实就是准确的值，我们需要得到的是这个真实值）加上加速度计的偏置、重力加速度（乘以world frame到body frame的转换）和加速度噪声项。
第二个式子等式左边是陀螺仪测量值，等式右边是陀螺仪真实值加上陀螺仪偏置和陀螺仪噪声项。这里的值都是IMU（body）帧坐标系下的。这里假设噪声是服从高斯正态分布，而偏置服从随机游走模型。

由上面最原始的式子积分就可以计算出下一时刻的p、v和q。将第 k 帧和第 k+1 帧之间的所有 IMU 进行积分，可得第 k+1 帧的位置、速度和旋转（PVQ），作为视觉估计的初始值，这里的旋转采用的四元数。

其中，和为IMU测量的加速度和角速度，是在Body自身坐标系，world坐标系是IMU所在的惯导系。

关于这部分目前还看不太懂。。。。先留一下，后面补充如何通过imu预计分，然后求解这三个量。。。

可参考：

https://mp.weixin.qq.com/s/opInITC_BDWz12j1_nUseA

https://blog.csdn.net/qq_41839222/article/details/86290941

初始化

在提取的图像的Features和做完IMU的预积分之后，进入了系统的初始化环节，那么系统为什么要进行初始化呢，主要的目的有以下两个：

系统使用单目相机，如果没有一个良好的尺度估计，就无法对两个传感器做进一步的融合。这个时候需要恢复出尺度；
要对IMU进行初始化，IMU会受到bias的影响，所以要得到IMU的bias。

所以我们要从初始化中恢复出尺度、重力、速度以及IMU的bias，因为视觉(SFM)在初始化的过程中有着较好的表现，所以在初始化的过程中主要以SFM为主，然后将IMU的预积分结果与其对齐，即可得到较好的初始化结果。首先，利用 SFM 进行纯视觉估计滑窗内所有帧的位姿及 3D 点逆深度，最后与 IMU 预积分进行对齐求解初始化参数。

先来探讨一下为什么需要初始化。之所以需要初始化的原因是：单目紧耦合的VIO是一个高度非线性系统，单目视觉没有尺度信息，IMU的测量又存在偏置误差，如果没有良好的初始值很难将这两种测量结果有机融合，因而初始化是VIO最脆弱的步骤。

首先单目是无法获得空间中的绝对尺度，而IMU又必然存在偏置，在后面进行求解的时候还需要用到重力加速度（包括大小和方向），对于速度比较敏感的条件下，比如说无人机，又要精确的速度信息，因此，如何有效的在紧耦合系统处理之前计算出这些量，对整个紧耦合系统的鲁棒性有着重大的意义（其实这里就可以理解成相机标定一样，没有正确的标定好相机的内参，相机在进行定位的时候必然不准，而且很有可能会挂掉）。所以初始化要做的事其实说起来很简单，就是计算出绝对尺度s、陀螺仪偏置bg、加速度偏置ba、重力加速度G和每个IMU时刻的速度v，VINS中重点说明了加速度计偏置值一般都会和重力加速度耦合到一起（也就是被重力加速度给吸收掉），重力加速度的量级要远大于其加速度偏置，而且在初始化时间内加速度计偏置比较小，很难真正的计算得到，因此忽略加速度计偏置的影响，在初始化中不再计算。初始化的作用是不言而喻的，直接影响整个紧耦合系统的鲁棒性以及定位精度，并且初始化一般都需要一个比较漫长的时间，VINS大概需要十秒左右。

VINS采用了视觉和IMU的松耦合初始化方案，首先用从运动恢复结构（SFM）得到纯视觉系统的初始化，即滑动窗口中所有帧的位姿和所有路标点的3d位置，然后将其与IMU预积分结果进行对齐，恢复尺度因子、重力、陀螺仪偏置和每一帧的速度。
系统的初始化主要包括三个环节：求取相机与IMU之间的相对旋转、相机初始化(局部滑窗内的SFM，包括没有尺度的BA)、IMU与视觉的对齐(IMU预积分中的 α等和相机的translation)。

相机与IMU之间的相对旋转

这个地方相当于求取相机与IMU的一部分外参。相机与IMU之间的旋转标定非常重要，偏差1-2°系统的精度就会变的极低。

纯视觉初始化（SFM）

这一阶段的思路就是单目相机的初始化过程，先求取本质矩阵求解位姿，进而三角化特征点，然后PnP求解位姿，不断重复的过程，直到恢复出滑窗内的Features和相机位姿

首先构建一个滑动窗口，包含一组数据帧。论文中提及使用的是对极几何模型的5点法求解单目相机的相对变换，包括相对旋转和无尺度信息的位移。其实基本上每个单目模型都是使用对极几何在初始化中求解两帧的相对变换，这里需要注意的是旋转是具有尺度不变性的（其实就是单位旋转，不会有尺度信息）。然后三角化得到相应的3d点坐标，有这些3d点和滑动窗口中其他的帧的2d点就可以进行PNP求解获得滑动窗口中的所有的位姿和特征点3d坐标，至此，纯视觉初始化就完成了。

视觉与IMU联合初始化（Visual-Inertia Alignment）

视觉与IMU的对齐主要解决三个问题：
(1) 修正陀螺仪的bias；
(2) 初始化速度、重力向量 gg和尺度因子(Metric scale)；
(3) 改进重力向量 gg的量值；

具体推导目前还看不懂，可以参考文章：https://www.cnblogs.com/buxiaoyi/p/8660854.html

关于初始化的参考文章：

https://blog.csdn.net/wangshuailpp/article/details/78719531

https://blog.csdn.net/qq_41839222/article/details/89106128

后端滑窗优化

将视觉约束、 IMU 约束和闭环约束放在一个大的目标函数中进行非线性优化，求解滑窗内所有帧的 PVQ、bias 等。

后端优化是VINS-Mono中除了初始化之外，创新性最高的一块，也是真真的 紧耦合 部分，而初始化的过程事实上是一个 松耦合。因为初始化过程中的状态量并没有放在最底层融合，而是各自做了位姿的计算，但是在后端优化的过程中，所有优化量都是在一起的。

前面所有提及的其实都是松耦合方式，目的是给整个系统提供优化初值和状态。所谓的紧耦合系统是将视觉和惯性的原始观测量进行有效的组合，也就是在数据处理前就进行数据融合，VINS中是将滑动窗口内的状态量整合到一个状态向量中，如下公式所示：

第一个式子是滑动窗口内整个状态向量，其中n是帧数，m是滑动窗口中的特征点总数。

第二个式子xk是在第k帧图像捕获到的IMU状态，包括位姿，速度，旋转，加速度计和陀螺仪偏置。

第三个式子是相机外参。

λ是特征点深度值的逆。从状态向量就可以看出xk只与IMU项以及Marginalization有关，特征点的深度值只与camera和Marginalization有关，所以下面建立BA紧耦合模型的时候按照这个思路，下面建立一个视觉惯性的BA优化模型以及鲁棒核函数模型：

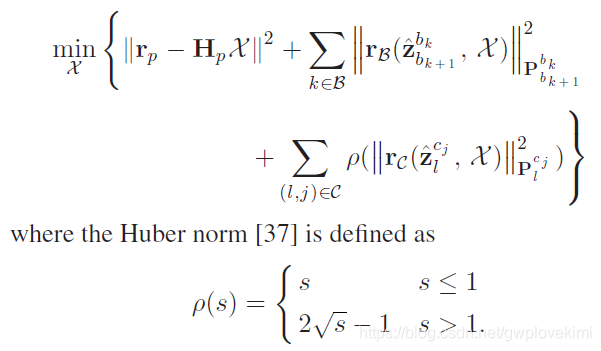
从公式中可以明显看出来，BA优化模型被分成了三个部分，分别是Marginalization（边缘化）残差部分（从滑动窗口中去掉的位姿和特征点的约束），IMU残差部分（滑动窗口中相邻帧间的IMU产生）和视觉代价误差函数部分（滑动窗口中特征点在相机下的投影产生），其中鲁棒核函数针对代价函数设定。

IMU观测值残差

闭环检测和优化

利用 DBoW 进行闭环检测，当检测成功后进行重定位，最后对整个相机轨迹进行闭环优化。

VINS-Mono的demo复现

工程连接在：https://github.com/HKUST-Aerial-Robotics/VINS-Mono

首先将代码导入工作空间并且编译

    cd ~/catkin_ws/src
    git clone https://github.com/HKUST-Aerial-Robotics/VINS-Mono.git
    cd ../
    catkin_make
    source ~/catkin_ws/devel/setup.bash

然后在公开的数据集上跑一下看看效果(数据集真的有点大～～～太慢了，后面用移动硬盘把这些数据集都存储一下方便后面使用)~

Download EuRoC MAV Dataset. Although it contains stereo cameras, we only use one camera. The system also works with ETH-asl cla dataset. We take EuRoC as the example.

选择Machine Hall 01的ROS bag进行下载，里面包含摄像头拍摄的视频帧图像、imu惯导信息，以及Ground-Truth真值等等。

运行下面代码来测试

    roslaunch vins_estimator euroc.launch 
    roslaunch vins_estimator vins_rviz.launch
    rosbag play YOUR_PATH_TO_DATASET/MH_01_easy.bag

运行下面代码来显示ground truth

roslaunch benchmark_publisher publish.launch  sequence_name:=MH_01_easy

绿色线是VINS的结果，红色线是ground truth

甚至可以直接运行EuRoC而不没有相机与imu的内参；作者已经实现了online calibrate

roslaunch vins_estimator euroc_no_extrinsic_param.launch
roslaunch vins_estimator vins_rviz.launch
rosbag play YOUR_PATH_TO_DATASET/MH_01_easy.bag

ou can even run EuRoC without extrinsic parameters between camera and IMU. We will calibrate them online. Replace the first command with:

地图融合

After playing MH_01 bag, you can continue playing MH_02 bag, MH_03 bag ... The system will merge them according to the loop closure.

3.3 map reuse

关于 map reuse 可以参考文章：
Relocalization, Global Optimization and Map Merging for Monocular Visual-Inertial SLAM

3.3.1 map save

Set the pose_graph_save_path in the config file (YOUR_VINS_FOLEDER/config/euroc/euroc_config.yaml). After playing MH_01 bag, input s in vins_estimator terminal, then enter. The current pose graph will be saved.

3.3.2 map load

Set the load_previous_pose_graph to 1 before doing 3.1.1. The system will load previous pose graph from pose_graph_save_path. Then you can play MH_02 bag. New sequence will be aligned to the previous pose graph.

看看其tf树

1、ar_demo：一个ar应用demo
2、benchmark_publisher：接收并发布数据集的基准值
3、camera_model
calib：相机参数标定
camera_models：各种相机模型类
chessboard：检测棋盘格
gpl
sparse_graph
intrinsic_calib.cc：相机标定模块main函数
4、config：系统配置文件存放处
5、feature_trackers：
feature_tracker_node.cpp ROS 节点函数，回调函数
feature_tracker.cpp 图像特征光流跟踪
6、pose_graph：
keyframe.cpp 关键帧选取、描述子计算与匹配
pose_graph.cpp 位姿图的建立与图优化
pose_graph_node.cpp ROS 节点函数，回调函数，主线程
7、support_files：帮助文档、Bow字典、Brief模板文件
8、vins_estimator
factor：实现IMU、camera等残差模型
initial：系统初始化，外参标定，SFM
utility：相机可视化，四元数等数据转换
estimator.cpp：紧耦合的VIO状态估计器实现
estimator_node.cpp：ROS 节点函数，回调函数，主线程
feature_manager.cpp：特征点管理，三角化，关键帧等
parameters.cpp：读取参数

VINS代码主要包含在两个文件中，分别是feature_tracker和vins_estimate，feature_tracker就像文件的名字一样，总体的作用是接收图像，使用KLT光流算法跟踪；vins_estimate包含相机和IMU数据的前端预处理（也就是预积分过程）、单目惯性联合初始化（在线的标定过程）、基于滑动窗口的BA联合优化、全局的图优化和回环检测等。