本章将介绍映射、函数、极限和函数的连续性等基本概念以及它们的一些性质。 ——高等数学同济版
目录
- 习题 1-1 映射与函数
- 习题 1-2 数列的极限
- 习题 1-3 函数的极限
- 习题1-4 无穷小与无穷大
- 习题1-5 极限运算法则
- 习题 1-6 极限存在准则 两个重要极限
- 习题 1-7 无穷小的比较
- 习题 1-8 函数的连续性与间断点
- 习题1-9 连续函数的运算与初等函数的连续性
- 4.求下列极限:
- (5) lim x → ∞ ( 3 + x 6 + x ) x − 1 2 \lim\limits_{x\to\infty}\left(\cfrac{3+x}{6+x}\right)^{\cfrac{x-1}{2}} x→∞lim(6+x3+x)2x−1;
- (6) lim x → 0 1 + tan x − 1 + sin x x 1 + sin 2 x − x \lim\limits_{x\to0}\cfrac{\sqrt{1+\tan x}-\sqrt{1+\sin x}}{x\sqrt{1+\sin^2x}-x} x→0limx1+sin2x−x1+tanx−1+sinx;
- (8) lim x → 0 e 3 x − e 2 x − e x + 1 ( 1 − x ) ( 1 + x ) 3 − 1 \lim\limits_{x\to0}\cfrac{e^{3x}-e^{2x}-e^x+1}{\sqrt[3]{(1-x)(1+x)}-1} x→0lim3(1−x)(1+x)−1e3x−e2x−ex+1;
- 5.设 f ( x ) f(x) f(x)在 R \mathbf R R上连续,且 f ( x ) ≠ 0 f(x)\ne0 f(x)=0, φ ( x ) \varphi(x) φ(x)在 R \mathbf R R上有定义,且有间断点,则下列陈述中,哪些是对的,哪些是错的?如果是对的,试说明理由;如果是错的,试给出一个反例。
- 习题1-10 闭区间上连续函数的性质
- 总习题一
- 9.求下列极限:
- 14.如果存在直线 L : y = k x + b L:y=kx+b L:y=kx+b,使得当 x → ∞ x\to\infty x→∞(或 x → + ∞ , x → − ∞ x\to+\infty,x\to-\infty x→+∞,x→−∞)时,曲线 y = f ( x ) y=f(x) y=f(x)上的动点 M ( x , y ) M(x,y) M(x,y)到直线 L L L的距离 d ( M , L ) → 0 d(M,L)\to0 d(M,L)→0,那么称 L L L为曲线 y = f ( x ) y=f(x) y=f(x)的渐近线。当直线 L L L的斜率 k ≠ 0 k\ne0 k=0时,称 L L L为斜渐近线。
- (1)证明:直线 L : y = k x + b L:y=kx+b L:y=kx+b为曲线 y = f ( x ) y=f(x) y=f(x)的渐近线的充分必要条件是 k = lim x → ∞ ( x → + ∞ x → − ∞ ) f ( x ) x , b = lim x → ∞ ( x → + ∞ x → − ∞ ) [ f ( x ) − k x ] ; k=\underset{\begin{pmatrix}x\to+\infty\\x\to-\infty\end{pmatrix}}{\lim\limits_{x\to\infty}}\cfrac{f(x)}{x},\qquad b=\underset{\begin{pmatrix}x\to+\infty\\x\to-\infty\end{pmatrix}}{\lim\limits_{x\to\infty}}[f(x)-kx]; k=(x→+∞x→−∞)x→∞limxf(x),b=(x→+∞x→−∞)x→∞lim[f(x)−kx];
- 写在最后
习题 1-1 映射与函数
映射是现代数学中的一个基本概念,而函数是微积分的研究对象,也是映射的一种。本节主要介绍映射、函数及有关概念、函数的性质与运算等。——高等数学同济版
本节主要介绍映射和函数的有关基础概念,相对简单。
习题 1-2 数列的极限
这一节主要介绍了数列极限的定义和收敛数列的性质。
3.下列关于数列 a n {a_n} an的极限是 a a a的定义那些是对的,哪些是错的?如果是对的,是说明理由;如果是错的,试给出一个反例。
(2)对于任意给定的 ε < 0 \varepsilon<0 ε<0,存在 N ∈ N + \mathit{N}\in\mathbf{N_+} N∈N+,当 n > N n>N n>N时,有无穷多项 x n x_n xn,使不等式 ∣ x n − a ∣ < ε |x_n-a|<\varepsilon ∣xn−a∣<ε成立;
解 错误;如对数列
x
n
=
{
n
,
n
=
2
k
−
1
,
1
−
1
n
,
n
=
2
k
,
k
∈
N
+
,
a
=
1.
x_n= \begin{cases} n,&n=2k-1,\\ 1-\frac {1}{n},&n=2k, \end{cases} \quad k\in\mathbf{N_+},\quad a=1.
xn={n,1−n1,n=2k−1,n=2k,k∈N+,a=1.
对任意给定的
ε
>
0
\varepsilon>0
ε>0(设
ε
<
1
\varepsilon<1
ε<1),存在
N
=
[
1
ε
]
N=[\ \cfrac {1}{\varepsilon}\ ]
N=[ ε1 ],当
n
>
N
n>N
n>N且
n
n
n为偶数时,
∣
x
n
−
a
∣
=
1
n
<
ε
|x_n-a|\ =\ \cfrac {1}{n}<\varepsilon
∣xn−a∣ = n1<ε成立,但
x
n
{x_n}
xn的极限不存在。(无穷多项满足不等于全部满足)
习题 1-3 函数的极限
这一节主要包括了函数极限的定义及基本性质,理解即可。
习题1-4 无穷小与无穷大
这一节主要介绍了无穷小和无穷大。
7.证明:函数 y = 1 x sin 1 x y=\cfrac {1}{x}\sin\cfrac{1}{x} y=x1sinx1在区间 ( 0 , 1 ] (0,1] (0,1]内无界,但这个函数不是 x → 0 + x\to0^+ x→0+时的无穷大。
证 先证函数
y
=
1
x
sin
1
x
y=\cfrac {1}{x}\sin\cfrac{1}{x}
y=x1sinx1在区间
(
0
,
1
]
(0,1]
(0,1]内无界。
因为
∀
M
>
0
\forall M>0
∀M>0,在区间
(
0
,
1
]
(0,1]
(0,1]中总可以找到点
x
0
x_0
x0,使
f
(
x
0
)
>
M
f(x_0)>M
f(x0)>M。例如可取
x
0
=
1
2
k
π
+
π
2
(
k
∈
N
)
x_0=\cfrac {1}{2k\pi+\cfrac {\pi}{2}}(k\isin\mathbf N)
x0=2kπ+2π1(k∈N),则
f
(
x
0
)
=
2
k
π
+
π
2
f(x_0)=2k\pi+\cfrac {\pi}{2}
f(x0)=2kπ+2π,当
k
k
k充分大时,可使
f
(
x
0
)
>
M
f(x_0)>M
f(x0)>M。所以
y
=
1
x
sin
1
x
y=\cfrac {1}{x}\sin\cfrac{1}{x}
y=x1sinx1在区间
(
0
,
1
]
(0,1]
(0,1]内无界。
再证函数 y = 1 x sin 1 x y=\cfrac {1}{x}\sin\cfrac{1}{x} y=x1sinx1不是 x → 0 + x\to0^+ x→0+时的无穷大。
因为 ∀ M > 0 \forall M>0 ∀M>0, δ > 0 \delta>0 δ>0,总可以找到点 x 0 x_0 x0,使 0 < x 0 < δ 0<x_0<\delta 0<x0<δ,但 f ( x 0 ) < M f(x_0)<M f(x0)<M。例如,可取 x 0 = 1 2 k π ( k ∈ N + ) x_0=\cfrac {1}{2k\pi}(k\isin\mathbf N_+) x0=2kπ1(k∈N+),当 k k k充分大时, 0 < x 0 < δ 0<x_0<\delta 0<x0<δ,但 f ( x 0 ) = 2 k π sin 2 k π = 0 < M f(x_0)=2k\pi \sin\ 2k\pi=0<M f(x0)=2kπsin 2kπ=0<M。所以, y = 1 x sin 1 x y=\cfrac {1}{x}\sin\cfrac{1}{x} y=x1sinx1不是 x → 0 + x\to0^+ x→0+时的无穷大。(这道题比较唬人,需要仔细分析题目才可以完成)
习题1-5 极限运算法则
本节讨论极限的求法,主要是建立极限的四则运算法则和复合函数的极限运算法则,利用这些法则,可以求某些函数的极限。——高等数学同济版
本节主要介绍了极限的四则运算法则和复合函数的极限运算法则。
习题 1-6 极限存在准则 两个重要极限
该节主要介绍了极限存在准则和 lim x → 0 sin x x = 1 \lim\limits_{x\to0}\cfrac {\sin x}{x}=1 x→0limxsinx=1及 lim x → ∞ ( 1 + 1 x ) x = e \lim\limits_{x\to\infty}\left(1+\cfrac{1}{x}\right)^x=e x→∞lim(1+x1)x=e。
习题 1-7 无穷小的比较
本节介绍了有关于无穷小的比较方法,包括了以下的常用替换公式。
当
x
→
0
x\to0
x→0时,以下公式成立:
sin
x
∼
x
1
−
cos
x
∼
1
2
x
2
tan
x
∼
x
arcsin
x
∼
x
arctan
x
∼
x
a
x
−
1
∼
x
ln
a
ln
(
x
+
1
)
∼
x
(
1
+
β
x
)
α
−
1
∼
1
+
α
β
x
x
−
sin
x
∼
x
3
6
log
a
(
1
+
x
)
∼
x
ln
a
\sin x\sim x\\ 1-\cos x\sim\cfrac {1}{2} x^2\\ \tan x\sim x\\ \arcsin x\sim x\\ \arctan x\sim x\\ a^x-1\sim x\ln a\\ \ln(x+1)\sim x\\ (1+\beta x)^\alpha-1\sim1+\alpha\beta x\\ x-\sin x\sim\frac{x^3}{6}\\ \log_a(1+x)\sim\frac{x}{\ln a}
sinx∼x1−cosx∼21x2tanx∼xarcsinx∼xarctanx∼xax−1∼xlnaln(x+1)∼x(1+βx)α−1∼1+αβxx−sinx∼6x3loga(1+x)∼lnax
5.利用等价无穷小的性质,求下列极限:
(4) lim x → 0 sin x − tan x ( 1 + x 2 3 − 1 ) ( 1 + sin x − 1 ) \lim\limits_{x\to 0}\cfrac{\sin x-\tan x}{(\sqrt[3]{1+x^2}-1)(\sqrt{1+\sin x}-1)} x→0lim(31+x2−1)(1+sinx−1)sinx−tanx
解
lim
x
→
0
sin
x
−
tan
x
(
1
+
x
2
3
−
1
)
(
1
+
sin
x
−
1
)
=
lim
x
→
0
sin
x
(
1
−
sec
x
)
1
3
x
2
⋅
1
2
sin
x
=
lim
x
→
0
−
1
2
x
2
1
6
x
2
=
−
3
\begin{aligned}\lim\limits_{x\to 0}\cfrac{\sin x-\tan x}{(\sqrt[3]{1+x^2}-1)(\sqrt{1+\sin x}-1)}&=\lim\limits_{x\to 0}\cfrac{\sin x(1-\sec x)}{\cfrac{1}{3}x^2\cdot\cfrac{1}{2}\sin x}\\ &=\lim\limits_{x\to 0}\cfrac{-\cfrac{1}{2}x^2}{\cfrac{1}{6}x^2}=-3\end{aligned}
x→0lim(31+x2−1)(1+sinx−1)sinx−tanx=x→0lim31x2⋅21sinxsinx(1−secx)=x→0lim61x2−21x2=−3
(这道题主要利用常用公式求解,否则不易想到求解方法)
习题 1-8 函数的连续性与间断点
这一节主要介绍了函数的连续性以及间断点的分类。
3.下列函数在指出的点出间断,说明这些间断点属于哪一类。如果使可去间断点,那么补充或改变函数的定义使它连续:
(2) y = x tan x , x = k π , x = k π + π 2 ( k = 0 , ± 1 , ± 2 … ) ; y=\cfrac{x}{\tan x},x=k\pi,x=k\pi+\cfrac{\pi}{2}\qquad(k=0,\pm1,\pm2\dots); y=tanxx,x=kπ,x=kπ+2π(k=0,±1,±2…);
解 对
x
=
0
x=0
x=0,因为
f
(
0
)
f(0)
f(0)无定义,
lim
x
→
0
x
tan
x
=
lim
x
→
0
x
x
=
1
\lim\limits_{x\to 0}\cfrac{x}{\tan x}=\lim\limits_{x\to 0}\cfrac{x}{x}=1
x→0limtanxx=x→0limxx=1,所以
x
=
0
x=0
x=0为第一类间断点(可去间断点),重新定义函数:
f
1
(
x
)
=
{
x
tan
x
,
x
≠
k
π
,
k
π
+
π
2
,
1
,
x
=
0
(
k
∈
Z
)
,
f_1(x)=\begin{cases} \cfrac{x}{\tan x},&x\neq k\pi,k\pi+\cfrac{\pi}{2},\\ 1,&x=0 \end{cases}\qquad (k\in\mathbf Z),
f1(x)=⎩⎨⎧tanxx,1,x=kπ,kπ+2π,x=0(k∈Z),
则
f
1
(
x
)
f_1(x)
f1(x)在
x
=
0
x=0
x=0处连续。
对
x
=
k
π
(
k
=
±
1
,
±
2
…
)
x=k\pi(k=\pm1,\pm2\dots)
x=kπ(k=±1,±2…),因为
lim
x
→
k
π
x
tan
x
=
∞
\lim\limits_{x\to k\pi}\cfrac{x}{\tan x}=\infty
x→kπlimtanxx=∞,所以
x
=
k
π
(
k
=
±
1
,
±
2
…
)
x=k\pi(k=\pm1,\pm2\dots)
x=kπ(k=±1,±2…)为第二类间断点(无穷间断点)。(由于
tan
x
\tan x
tanx可以有取值,这里容易误认为
x
=
k
π
(
k
=
±
1
,
±
2
…
)
x=k\pi(k=\pm1,\pm2\dots)
x=kπ(k=±1,±2…)也为第一类间断点)
对
x
=
k
π
+
π
2
(
k
∈
Z
)
x=k\pi+\cfrac{\pi}{2} (k\in\mathbf Z)
x=kπ+2π(k∈Z),因为
lim
x
→
k
π
+
π
2
x
tan
x
=
0
\lim\limits_{x\to k\pi+\frac{\pi}{2}}\cfrac{x}{\tan x}=0
x→kπ+2πlimtanxx=0,而函数在
k
π
+
π
2
k\pi+\cfrac{\pi}{2}
kπ+2π处无意义,所以
x
=
k
π
+
π
2
(
k
∈
Z
)
x=k\pi+\cfrac{\pi}{2} (k\in\mathbf Z)
x=kπ+2π(k∈Z)为第一类间断点(可去间断点),重新定义函数:
f
2
(
x
)
=
{
x
tan
x
,
x
≠
k
π
,
k
π
+
π
2
,
0
,
x
=
k
π
+
π
2
(
k
∈
Z
)
,
f_2(x)=\begin{cases} \cfrac{x}{\tan x},&x\neq k\pi,k\pi+\cfrac{\pi}{2},\\ 0,&x=k\pi+\cfrac{\pi}{2} \end{cases}\qquad (k\in\mathbf Z),
f2(x)=⎩⎪⎨⎪⎧tanxx,0,x=kπ,kπ+2π,x=kπ+2π(k∈Z),
则
f
2
(
x
)
f_2(x)
f2(x)在
x
=
k
π
+
π
2
(
k
∈
Z
)
x=k\pi+\cfrac{\pi}{2} (k\in\mathbf Z)
x=kπ+2π(k∈Z)处连续。(这里由于
tan
x
\tan x
tanx取不到值,可能误认为该处为第二类间断点)
习题1-9 连续函数的运算与初等函数的连续性
本节介绍较为复杂的连续性证明以及在间断点处的极限求解,较难。
4.求下列极限:
(5) lim x → ∞ ( 3 + x 6 + x ) x − 1 2 \lim\limits_{x\to\infty}\left(\cfrac{3+x}{6+x}\right)^{\cfrac{x-1}{2}} x→∞lim(6+x3+x)2x−1;
解
lim
x
→
∞
(
3
+
x
6
+
x
)
x
−
1
2
=
lim
x
→
∞
[
(
1
−
3
6
+
x
)
−
6
+
x
3
]
−
3
2
⋅
lim
x
→
∞
(
1
−
3
6
+
x
)
−
7
2
=
e
−
3
2
.
\lim\limits_{x\to\infty}\left(\cfrac{3+x}{6+x}\right)^{\cfrac{x-1}{2}}=\lim\limits_{x\to\infty}\left[\left(1-\cfrac{3}{6+x}\right)^{-\cfrac{6+x}{3}}\right]^{-\cfrac{3}{2}}\cdot\lim\limits_{x\to\infty}\left(1-\cfrac{3}{6+x}\right)^{-\cfrac{7}{2}}=e^{-\frac{3}{2}}.
x→∞lim(6+x3+x)2x−1=x→∞lim⎣⎢⎢⎢⎡(1−6+x3)−36+x⎦⎥⎥⎥⎤−23⋅x→∞lim(1−6+x3)−27=e−23.
(6) lim x → 0 1 + tan x − 1 + sin x x 1 + sin 2 x − x \lim\limits_{x\to0}\cfrac{\sqrt{1+\tan x}-\sqrt{1+\sin x}}{x\sqrt{1+\sin^2x}-x} x→0limx1+sin2x−x1+tanx−1+sinx;
解
lim
x
→
0
1
+
tan
x
−
1
+
sin
x
x
1
+
sin
2
x
−
x
=
lim
x
→
0
tan
x
−
sin
x
x
(
1
+
sin
2
x
−
1
)
(
1
+
tan
x
+
1
+
sin
x
)
=
lim
x
→
0
(
sin
x
x
⋅
sec
x
−
1
1
+
sin
2
x
−
1
⋅
1
1
+
tan
x
+
1
+
sin
x
)
=
lim
x
→
0
sin
x
x
⋅
lim
x
→
0
1
2
x
2
1
2
sin
2
x
⋅
lim
x
→
0
1
1
+
tan
x
+
1
+
sin
x
=
1
⋅
1
⋅
1
2
=
1
2
.
\begin{aligned}\lim\limits_{x\to0}\cfrac{\sqrt{1+\tan x}-\sqrt{1+\sin x}}{x\sqrt{1+\sin^2x}-x}&=\lim\limits_{x\to0}\cfrac{\tan x-\sin x}{x(\sqrt{1+\sin^2x}-1)(\sqrt{1+\tan x}+\sqrt{1+\sin x})}\\ &=\lim\limits_{x\to0}(\cfrac{\sin x}{x}\cdot\cfrac{\sec x-1}{\sqrt{1+\sin^2x}-1}\cdot\cfrac{1}{\sqrt{1+\tan x}+\sqrt{1+\sin x}})\\ &=\lim\limits_{x\to0}\cfrac{\sin x}{x}\cdot\lim\limits_{x\to0}\cfrac{\cfrac{1}{2}x^2}{\cfrac{1}{2}\sin^2x}\cdot\lim\limits_{x\to0}\cfrac{1}{\sqrt{1+\tan x}+\sqrt{1+\sin x}}\\ &=1\cdot1\cdot\cfrac{1}{2}=\cfrac{1}{2}.\end{aligned}
x→0limx1+sin2x−x1+tanx−1+sinx=x→0limx(1+sin2x−1)(1+tanx+1+sinx)tanx−sinx=x→0lim(xsinx⋅1+sin2x−1secx−1⋅1+tanx+1+sinx1)=x→0limxsinx⋅x→0lim21sin2x21x2⋅x→0lim1+tanx+1+sinx1=1⋅1⋅21=21.
(8) lim x → 0 e 3 x − e 2 x − e x + 1 ( 1 − x ) ( 1 + x ) 3 − 1 \lim\limits_{x\to0}\cfrac{e^{3x}-e^{2x}-e^x+1}{\sqrt[3]{(1-x)(1+x)}-1} x→0lim3(1−x)(1+x)−1e3x−e2x−ex+1;
解
lim
x
→
0
e
3
x
−
e
2
x
−
e
x
+
1
(
1
−
x
)
(
1
+
x
)
3
−
1
=
lim
x
→
0
(
e
2
x
−
1
)
(
e
x
−
1
)
(
1
−
x
2
)
1
3
−
1
=
lim
x
→
0
2
x
⋅
x
−
1
3
x
2
=
−
6.
\lim\limits_{x\to0}\cfrac{e^{3x}-e^{2x}-e^x+1}{\sqrt[3]{(1-x)(1+x)}-1}=\lim\limits_{x\to0}\cfrac{(e^{2x}-1)(e^x-1)}{(1-x^2)^{\frac{1}{3}}-1}=\lim\limits_{x\to0}\cfrac{2x\cdot x}{-\cfrac{1}{3}x^2}=-6.
x→0lim3(1−x)(1+x)−1e3x−e2x−ex+1=x→0lim(1−x2)31−1(e2x−1)(ex−1)=x→0lim−31x22x⋅x=−6.
(这方面主要涉及到分解因式和等价无穷小替换,要多练习)
5.设 f ( x ) f(x) f(x)在 R \mathbf R R上连续,且 f ( x ) ≠ 0 f(x)\ne0 f(x)=0, φ ( x ) \varphi(x) φ(x)在 R \mathbf R R上有定义,且有间断点,则下列陈述中,哪些是对的,哪些是错的?如果是对的,试说明理由;如果是错的,试给出一个反例。
(1) φ [ f ( x ) ] \varphi[f(x)] φ[f(x)]必有间断点;
解 错。例如, φ ( x ) = sgn x , f ( x ) = e x , φ [ f ( x ) ] ≡ 1 \varphi(x)=\mathinner{\text{sgn}} x,f(x)=e^x,\varphi[f(x)]\equiv1 φ(x)=sgnx,f(x)=ex,φ[f(x)]≡1在 R \mathbf R R上处处连续。(这个情况比较少见,很难想到)
习题1-10 闭区间上连续函数的性质
在闭区间上连续的函数有几个重要的性质,今以定理的形式叙述它们。——高等数学同济版
这一节主要讲述了有关于函数连续的几个重要性质。
4.证明任一最高次幂的指数为奇数的代数方程 a 0 x 2 n + 1 + a 1 x 2 n + ⋯ + a 2 n x + a 2 n + 1 = 0 a_0x^{2n+1}+a_1x^{2n}+\cdots+a_{2n}x+a_{2n+1}=0 a0x2n+1+a1x2n+⋯+a2nx+a2n+1=0至少有一实根,其中 a 0 , a 1 , ⋯ , a 2 n + 1 a_0,a_1,\cdots,a_{2n+1} a0,a1,⋯,a2n+1均为常数, n ∈ N n\in\mathbf N n∈N
证 当 x x x的绝对值充分大时, f ( x ) = a 0 x 2 n + 1 + a 1 x 2 n + ⋯ + a 2 n x + a 2 n + 1 f(x)=a_0x^{2n+1}+a_1x^{2n}+\cdots+a_{2n}x+a_{2n+1} f(x)=a0x2n+1+a1x2n+⋯+a2nx+a2n+1的符号取决于 a 0 a_0 a0的符号,即当 x x x为正与 a 0 a_0 a0同号,当 x x x为负与 a 0 a_0 a0异号,且 a 0 ≠ 0 a_0\ne0 a0=0。因 f ( x ) f(x) f(x)是连续函数,它在某充分大的区间的两端处异号,由零点定理可知它在某一区间内某一点处必定为零,故方程 a 0 x 2 n + 1 + a 1 x 2 n + ⋯ + a 2 n x + a 2 n + 1 = 0 a_0x^{2n+1}+a_1x^{2n}+\cdots+a_{2n}x+a_{2n+1}=0 a0x2n+1+a1x2n+⋯+a2nx+a2n+1=0至少有一实根。(个人认为这个证明并不严谨,过于简单,意思很明白但不太符合数学规范,答案给的是这个。)
总习题一
9.求下列极限:
(5) lim x → 0 ( a x + b x + c x 3 ) 1 x . \lim\limits_{x\to0}\left(\cfrac{a^x+b^x+c^x}{3}\right)^{\frac{1}{x}}. x→0lim(3ax+bx+cx)x1.
解 因为
(
a
x
+
b
x
+
c
x
3
)
1
x
=
(
1
+
a
x
+
b
x
+
c
x
−
3
3
)
3
a
x
+
b
x
+
c
x
−
3
⋅
1
3
(
a
x
−
1
x
+
b
x
−
1
x
+
c
x
−
1
x
)
,
\left(\cfrac{a^x+b^x+c^x}{3}\right)^{\frac{1}{x}}=\left(1+\cfrac{a^x+b^x+c^x-3}{3}\right)^{\cfrac{3}{a^x+b^x+c^x-3}\cdot\frac{1}{3}\left(\cfrac{a^x-1}{x}+\cfrac{b^x-1}{x}+\cfrac{c^x-1}{x}\right)},
(3ax+bx+cx)x1=(1+3ax+bx+cx−3)ax+bx+cx−33⋅31(xax−1+xbx−1+xcx−1),
而
(
1
+
a
x
+
b
x
+
c
x
−
3
3
)
3
a
x
+
b
x
+
c
x
−
3
→
e
(
x
→
0
)
,
a
x
−
1
x
→
ln
a
,
b
x
−
1
x
→
ln
b
,
c
x
−
1
x
→
ln
c
(
x
→
0
)
,
\left(1+\cfrac{a^x+b^x+c^x-3}{3}\right)^{\cfrac{3}{a^x+b^x+c^x-3}}\to e(x\to0),\\ \cfrac{a^x-1}{x}\to\ln a,\qquad\cfrac{b^x-1}{x}\to\ln b,\qquad\cfrac{c^x-1}{x}\to\ln c(x\to0),
(1+3ax+bx+cx−3)ax+bx+cx−33→e(x→0),xax−1→lna,xbx−1→lnb,xcx−1→lnc(x→0),
所以
lim
x
→
0
(
a
x
+
b
x
+
c
x
3
)
1
x
=
e
1
3
(
ln
a
+
ln
b
+
ln
c
)
=
(
a
b
c
)
1
3
.
\lim\limits_{x\to0}\left(\cfrac{a^x+b^x+c^x}{3}\right)^{\cfrac{1}{x}}=e^{\frac{1}{3}(\ln a+\ln b+\ln c)}=(abc)^{\frac{1}{3}}.
x→0lim(3ax+bx+cx)x1=e31(lna+lnb+lnc)=(abc)31.
(这道题代换有点复杂,能想清楚代换过程即可)
14.如果存在直线 L : y = k x + b L:y=kx+b L:y=kx+b,使得当 x → ∞ x\to\infty x→∞(或 x → + ∞ , x → − ∞ x\to+\infty,x\to-\infty x→+∞,x→−∞)时,曲线 y = f ( x ) y=f(x) y=f(x)上的动点 M ( x , y ) M(x,y) M(x,y)到直线 L L L的距离 d ( M , L ) → 0 d(M,L)\to0 d(M,L)→0,那么称 L L L为曲线 y = f ( x ) y=f(x) y=f(x)的渐近线。当直线 L L L的斜率 k ≠ 0 k\ne0 k=0时,称 L L L为斜渐近线。
(1)证明:直线 L : y = k x + b L:y=kx+b L:y=kx+b为曲线 y = f ( x ) y=f(x) y=f(x)的渐近线的充分必要条件是 k = lim x → ∞ ( x → + ∞ x → − ∞ ) f ( x ) x , b = lim x → ∞ ( x → + ∞ x → − ∞ ) [ f ( x ) − k x ] ; k=\underset{\begin{pmatrix}x\to+\infty\\x\to-\infty\end{pmatrix}}{\lim\limits_{x\to\infty}}\cfrac{f(x)}{x},\qquad b=\underset{\begin{pmatrix}x\to+\infty\\x\to-\infty\end{pmatrix}}{\lim\limits_{x\to\infty}}[f(x)-kx]; k=(x→+∞x→−∞)x→∞limxf(x),b=(x→+∞x→−∞)x→∞lim[f(x)−kx];
解 就
x
→
+
∞
x\to+\infty
x→+∞的情形证明,其他情况类似。
设
L
:
y
=
k
x
+
b
L:y=kx+b
L:y=kx+b为曲线
y
=
f
(
x
)
y=f(x)
y=f(x)的渐近线。
1
。
1^。
1。若
k
≠
0
k\ne0
k=0,如下图所示,
k
=
tan
α
k=\tan\alpha
k=tanα(
α
\alpha
α为
L
L
L的倾角,
α
≠
π
2
\alpha\ne\cfrac{\pi}{2}
α=2π),曲线
y
=
f
(
x
)
y=f(x)
y=f(x)上的动点
M
(
x
,
y
)
M(x,y)
M(x,y)到直线
L
L
L的距离为
∣
M
K
∣
|MK|
∣MK∣。过
M
M
M作横轴的垂线,叫直线
L
L
L于
K
1
K_1
K1,则
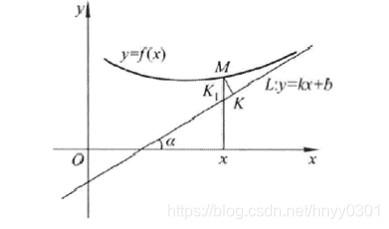
∣
M
K
1
∣
=
∣
M
K
∣
cos
α
.
|MK_1|=\cfrac{|MK|}{\cos\alpha}.
∣MK1∣=cosα∣MK∣.
显然
∣
M
K
∣
→
0
(
x
→
+
∞
)
|MK|\to0(x\to+\infty)
∣MK∣→0(x→+∞)与
∣
M
K
1
∣
→
0
(
x
→
+
∞
)
|MK_1|\to0(x\to+\infty)
∣MK1∣→0(x→+∞)等价,而
∣
M
K
1
∣
=
∣
f
(
x
)
−
(
k
x
+
b
)
∣
.
|MK_1|=|f(x)-(kx+b)|.
∣MK1∣=∣f(x)−(kx+b)∣.
因为
L
:
y
=
k
x
+
b
L:y=kx+b
L:y=kx+b是曲线
y
=
f
(
x
)
y=f(x)
y=f(x)的渐近线。所以
∣
M
K
∣
→
0
(
x
→
+
∞
)
⇒
∣
M
K
1
∣
→
0
(
x
→
+
∞
)
,
|MK|\to0(x\to+\infty)\Rightarrow|MK_1|\to0(x\to+\infty),
∣MK∣→0(x→+∞)⇒∣MK1∣→0(x→+∞),
即
lim
x
→
+
∞
[
f
(
x
)
−
(
k
x
+
b
)
]
=
0
,
(
1
)
\begin{matrix} \lim\limits_{x\to+\infty}[f(x)-(kx+b)]=0,&\qquad(1) \end{matrix}
x→+∞lim[f(x)−(kx+b)]=0,(1)
从而
k
=
lim
x
→
∞
f
(
x
)
x
,
b
=
lim
x
→
∞
[
f
(
x
)
−
k
x
]
\begin{aligned} k&=\lim\limits_{x\to\infty}\cfrac{f(x)}{x},\qquad \\b&=\lim\limits_{x\to\infty}[f(x)-kx] \end{aligned}
kb=x→∞limxf(x),=x→∞lim[f(x)−kx]
(在考纲上明确要求会求函数的水平、垂直及斜渐近线,但斜渐近线只有在第一章题目中明确提及定义和求法,记录于此作为提醒)
写在最后
如果觉得文章不错就点个赞吧。另外,如果有不同的观点,欢迎留言或私信。
欢迎非商业转载,转载请注明出处。
























 398
398











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








