第一章机械臂基础-1.1 位姿描述与坐标变换

愈之~

已于 2024-07-05 13:52:15 修改

阅读量895

点赞数 10

分类专栏：机械臂算法仿真笔记文章标签：算法

于 2024-07-05 13:46:55 首次发布

本文链接：https://blog.csdn.net/hq1215758640/article/details/140183428

版权

机械臂算法仿真笔记专栏收录该内容

7 篇文章 1 订阅

订阅专栏

（一）位姿描述

空间中的一个物体，或者一个点，固定好坐标系之后，就有一个位置坐标，可以用3x1的位置矢量来描述，当然也可以建立多个坐标系，那么对于一个点来说，在不同的坐标系下就有不同的位置坐标，因此需要注明此点在哪个坐标系下的位置坐标，例如，在坐标系 $A$ $A$ 下面的某个点，那么可以通过 $_{}^{A}\textrm{P}$ 来表示，如图1.1.1所示：

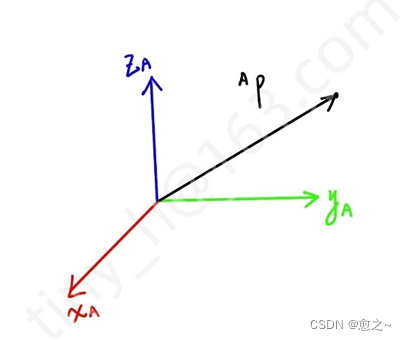
图1.1.1 空间一点的位置表示

$_{}^{A}\textrm{P}\ = [P_x \ P_y\ P_z]^T$ (1-1-1)

其中 $P_x,P_y, P_z$ 分别为三个坐标系上的坐标分量，也可以认为是三个坐标轴上的投影。除了空间中的位置坐标外，还需要表示空间中物体的姿态，为了表示空间中的物体姿态，需将坐标系 $B$ 固定在物体上，并将此时的B 坐标系的三个轴向组成的单位矩阵作为物体 $B$ 的姿态

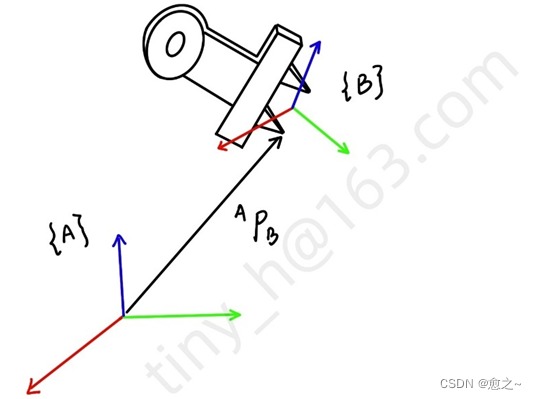
图1.1.2 空间物体的姿态

$\ _B^AR=\begin{bmatrix} _.^A{\widehat X}_B & _.^A{\widehat Y}_B& _.^A{\widehat Z}_B \end{bmatrix}=\begin{bmatrix} r_{11} & r_{12} & r_{13} \\ r_{21} &r_{22} &r_{23} \\ r_{31} & r_{32} & r_{33} \end{bmatrix}$ (1-1-2)

此时旋转矩阵 ${_B^A}R$ 的每一列矢量，表示为 $B$ 坐标系的x、y、z轴分别在坐标系 $A$ 下的各个轴向上的投影，也可以理解为 $B$ 坐标系下各个轴向与 $A$ 坐标系下的各个轴的点积形式

$\ _B^AR=\begin{bmatrix} _.^A{\widehat X}_B & _.^A{\widehat Y}_B& _.^A{\widehat Z}_B \end{bmatrix}=\begin{bmatrix} \widehat X_B\cdot \widehat X_A & \widehat Y_B\cdot \widehat X_A & \widehat Z_B\cdot \widehat X_A \\ \widehat X_B\cdot \widehat Y_A &\widehat Y_B\cdot \widehat Y_A &\widehat Z_B\cdot \widehat Y_A\\ \widehat X_B\cdot \widehat Z_A & \widehat Y_B\cdot \widehat Z_A &\widehat Z_B\cdot \widehat Z_A \end{bmatrix}$ (1-1-3)

或者

$\ _B^AR=\begin{bmatrix} n\cdot x & o\cdot x& a\cdot x\\ n\cdot y & o\cdot y& a\cdot y \\ n\cdot z & o\cdot z& a\cdot z \end{bmatrix} = \begin{bmatrix} cos(n,x) & cos(o,x) & cos(a,x) \\ cos(n,y)& cos(o,y) & cos(a,y)\\ cos(n,z) & cos(o,z) & cos(a,z) \end{bmatrix}$ (1-1-4)

其中[n,o,a]，[x,y,z] 分别坐标系 $A$ 和 $B$ 的各个轴的单位矢量。

另外也可以看出 $\ _B^AR=\begin{bmatrix} _.^A{\widehat X}_B & _.^A{\widehat Y}_B& _.^A{\widehat Z}_B \end{bmatrix} = \begin{bmatrix} _.^A{\widehat X}_B^T \\ _.^A{\widehat Y}_B^T\\ _.^A{\widehat Z}_B^T \end{bmatrix}$ 因此 $\ _B^AR$ 为坐标系 $A$ 相对于坐标系 $B$ 的描述，由此可得到 ${_A^B}R=\ {{_B^A}R}^T$ ，并由此可以得到

${_A^B}R\bullet{{_B^A}R}^T=\ I$ (1-1-5)

$I$ 为3x3的单位矩阵，所以

${_B^A}R={{_A^B}R}^T=\ {{_A^B}R}^{-1}$ (1-1-6)

上面的方程公式中，分别阐述了位置和姿态的表示方法，那么一个完成的描述需要将位置与姿态整合，形成新的位姿矩阵，姿态为3x3的单位矩阵，而在机器人中，经常加上一个位置的列矢量，形成新的位姿矩阵，例如在图1.1.2中，将 ${_B^A}R$ 表示抓手相对于{ $A$ }坐标系的姿态，而将 $_{}^{A}\textrm{P}$ 或者 $_{}^{A}\textrm{P}_{BORG}$ 来表示{ $B$ }坐标系原点相对于 $A$ 坐标系的位置信息。因此也可以说物体的位姿为：

$T=\left\{{_B^A}R,_{}^{A}\textrm{P}_{BORG}\right\}$ (1-1-7)

（二）坐标变换

很多时候，空间中的位姿是固定的，但是需要在不同的参考坐标系下描述同一位姿，那么坐标系与坐标系之间的转换尤其重要，打通各个坐标系之间的转换之后，就能在后续的计算过程中简化问题。

考虑到空间中有两个坐标系 ${A}$ 和坐标系 $B$ ，若两坐标系之间姿态相同，也就是说两坐标系轴向x,y,z平行且方向相同，那么就有以下方程，参考图1.1.3：

$_{}^{A}\textrm{P} = _{}^{A}\textrm{P}_{BORG}+_{}^{B}\textrm{P}$ (1-1-8)

图1.1.3 坐标系姿态相同时的坐标变换

或者写成

$_{}^{A/A}\textrm{P} = _{}^{A/A}\textrm{P}_{BORG}+_{}^{B/B}\textrm{P}$ (1-1-9)

这里解释一下，公式（1-1-8）这里很简单，因为姿态的相同，可以看成同一坐标系下的两个矢量相加，这里就不赘述了。公式（1-1-9）可以看到 $P$ 的左上角有俩个 $A$ 或者 $B$ ，这里表示相对坐标系和描述坐标系，例如 $_{}^{A2/A1}\textrm{P} _Q$ ，那么此符号的含义为，点 $Q$ 相对于坐标系{ $A_1$ }在坐标系{ $A_2$ }下的描述，可以理解为，“点 $Q$ 相对于坐标系{ $A_1$ }“表示 $Q$ 点在{ $A_1$ }下的矢量，“在坐标系{ $A_2$ }下的描述”表示空间中的矢量，在不同坐标系下的描述不同，这里指定描述坐标系{ $A_2$ }，这样能更加准确的表述空间中点的位姿，以避免后续中有些符号导致的难以理解。

若考虑到两坐标系{ $A$ }和{ $B$ }，它们的坐标系原点重合，都在同一个点上，而坐标系轴向不同，如下图1.1.4所示

图1.1.4 坐标系位置相同时的坐标变换

那么就有

$_{}^{A/A}\textrm{P} ={_B^A}R \cdot _{}^{B/B}\textrm{P}$ (1-1-10)

如果在空间中，同时考虑到两个坐标系有位置变换跟姿态变化的话，那么将公式（1-1-9）和公式（1-1-10）结合得到

$_{}^{A/A}\textrm{P} ={_B^A}R \cdot _{}^{B/B}\textrm{P} +_{}^{A/A}\textrm{P}_{BORG}$ (1-1-11)

将上式（1-1-10）写成矩阵形式得到：

$\begin{bmatrix} ^{A/A}P\\ 1 \end{bmatrix} = \begin{bmatrix} _B^AR & ^{A/A}P_{BORG}\\ 0& 1 \end{bmatrix}\cdot \begin{bmatrix} ^{B/B}P\\ 1 \end{bmatrix}$ (1-1-12)

并简写成

$_{}^{A/A}\textrm{P} ={_B^A}T \cdot _{}^{B/B}\textrm{P}$ (1-1-13)

上式中的 ${_B^A}T$ 被称为齐次变换矩阵，这里可以看成矩阵形式的转换来表示空间中的变换关系。非齐次变换矩阵有最后的一行不是[0 0 0 1]，属于透视变换和缩放变换。前三个0表示透视，最后一个1表示缩放，在视觉相机领域中经常会用到这种非齐次变换矩阵，这里不做详细探讨。另外公式（1-1-13）、（1-1-11）与公式(1-1-7)相似，这表明空间中的位姿其实也一种空间变换，都是描述空间坐标系与相对坐标系、相对坐标系与物体之间的关系，坐标变换也是位姿，位姿也是坐标变换。

（三）平移算子与旋转算子

将空间中的一个点沿着已知的方向平移，对于空间中的移动仅一个坐标系，或者说相同姿态坐标系下的移动，那么可以有

$_{}^{A/A}\textrm{P}_2 =_{}^{A/A}\textrm{P}_1 +_{}^{A/A}\textrm{Q}$ (1-1-14)

这里写成矩阵形式

$_{}^{A/A}\textrm{P}_2 =D_Q(q)\cdot _{}^{A/A}\textrm{P}_1$ (1-1-15)

其中 $q$ 是沿着矢量 $Q$ 方向的平移距离，那么根据上式可以得知矩阵 $D_Q(q)$ 只有第四列有值，其他要么为0要么为单位矩阵。

$D_Q\left(q\right)=\ \left[\begin{matrix}1&0&\begin{matrix}0&q_x\\\end{matrix}\\0&1&\begin{matrix}0&q_y\\\end{matrix}\\\begin{matrix}0\\0\\\end{matrix}&\begin{matrix}0\\0\\\end{matrix}&\begin{matrix}\begin{matrix}1\\0\\\end{matrix}&\begin{matrix}q_z\\1\\\end{matrix}\\\end{matrix}\\\end{matrix}\right]$ (1-1-16)

这里称 $D_Q\left(q\right)$ 为平移算子。

图1.1.5 平移算子

同样根据前面公式（1-1-15）可以写成旋转算子

$_{}^{A/A}\textrm{P}_2 =R_k(\theta)\cdot _{}^{A/A}\textrm{P}_1$ (1-1-17)

这里跟公式（1-1-16）的区别在于，矩阵的前三行三列不为单位矩阵，而平移的第四列为0

$R_k(\theta)=\ \left[\begin{matrix}n_x(\theta)&o_x(\theta)&\begin{matrix}a_x(\theta)&0\\\end{matrix}\\n_y(\theta)&o_y(\theta)&\begin{matrix}a_y(\theta)&0\\\end{matrix}\\\begin{matrix}n_z(\theta)\\0\\\end{matrix}&\begin{matrix}o_z(\theta)\\0\\\end{matrix}&\begin{matrix}\begin{matrix}a_z(\theta)\\0\\\end{matrix}&\begin{matrix}0\\1\\\end{matrix}\\\end{matrix}\\\end{matrix}\right]$ (1-1-18)

$R_k(\theta)$ 为旋转算子，关于空间中的 $k$ 矢量轴旋转 $\theta$ ，下面有三种特殊旋转算子，就是关于x轴、y轴、z轴旋转 $\theta$ ，那么就有

$R_X(\theta)=\begin{bmatrix} 1 & 0 &0 \\ 0 & c\theta& -s\theta\\ 0&s\theta & c\theta \end{bmatrix}$

$R_Y(\theta)=\begin{bmatrix} c\theta & 0 &s\theta \\ 0 & 1& 0\\ -s\theta&0 & c\theta \end{bmatrix}$

$R_Z(\theta)=\begin{bmatrix} c\theta & -s\theta &0 \\ s\theta & c\theta& 0\\ 0&0 & 1 \end{bmatrix}$ (1-1-19)

式中： $s\theta=sin{(}\theta),c\theta=cos{(}\theta)$ .

最终，结合平移和旋转来说，矢量 $_{}^{A/A}\textrm{P}_1$ 经过平移和旋转之后，得到新的矢量，可以用齐次变换矩阵来描述：

$^{A/A}P_2 = T\cdot ^{A/A}P_1$ (1-1-20)

其中 $T=[\begin{matrix}R_k(\theta) & {^{A/A}}Q\\0&1\\\end{matrix}]$ 。

（四）混合变换或变换方程

在图1.1.6中，已知 $_C^BT$ 、 $_B^AT$ 和 $^{C/C}P$ ，求 $^{A/A}P$ ，计算如下：将B坐标系作为中间过渡，那么先求 $^{B/B}P$ ：

${^{B/B}}P= {_C^B}T\bullet {^{C/C}}P$ (1-1-21)

同理可求得

${^{A/A}}P={_B^A}T\bullet\ {^{B/B}}P$ (1-1-22)

图1.1.6 混合变换

将（1-1-21）带入（1-1-22）中得到

${^{A/A}}P={_B^A}T\bullet\ {_C^B}T\bullet\ {^{C/C}}P$ (1-1-23)

由此可以定义：

$\ _C^AT=_B^AT\bullet_C^BT$ (1-1-24)

最后得出

$\ _C^AT=\left[\begin{matrix}\ _B^AR_C^BR&\ _B^AR^{B/B}P_{CORG}+^{A/A}P_{BORG}\\0&1\\\end{matrix}\right]$ (1-1-25)

也就是说，空间中从一个坐标系到另一个坐标系之间的转换其实就是矩阵的乘法或者逆转换的关系，从公式（1-1-24）中可以看出，坐标系{ $B$ } 和{ $C$ }之间的转换、{ $A$ }和{ $B$ } 之间的转换，通过矩阵的乘法，最后转成了{ $A$ } 和{ $C$ } 之间的转换。另外两坐标系之间的转换假如为 $T$ ，那么两坐标系之间的相反的转换就为 $T^T$ 或者 $T^{-1}$ ,那么可以得知，知道三个坐标系之间的转换关系，例如图1.1.6中的{ $A$ }、{ $B$ } 、{ $C$ } ，若在任意两个坐标系之间插入一个平移算子或者旋转算子，那么三个坐标系之间的动态变换其实就已经决定，例如 $\ _C^AT=_B^AT_C^BT$ ，在{ $B$ } 坐标系的后面插入一个旋转算子， $T_x(\theta)$ ，这里是4x4矩阵， $T_X(\theta)=\ \left[\begin{matrix}R_x(\theta)&0\\0&1\\\end{matrix}\right]$ 那么表达式为

$_C^AT=_B^A{T\bullet T_X(\theta)\bullet}_C^BT$ (1-1-26)

那么可以试想一下，坐标系{ $C$ }会有什么变化，可以预料得到坐标系{ $C$ }将会围绕着{ $B$ } 的 $X$ 轴旋转 $\theta$ 角度，若这个 $\theta$ 是一个时间的函数，那么坐标系{ $C$ } 将会随着时间的变化围绕着{ $B$ } 旋转。同样，若想要{ $A$ } 坐标系围绕着{ $C$ } 坐标系旋转，那么表达式该如何去写？答案是 $\ _A^BT=_C^B{T\bullet T_X(\theta)\bullet}_A^CT$ ，这里的 $\ _A^BT=\ {{_B^A}T}^{-1}=\ {{_B^A}T}^T$ , $\ _C^AT={\ _A^CT}^T=\ {\ _A^CT}^{-1}$ ,由此可以看出坐标系之间根据乘法相关规则，可以让坐标系做出相应的变化，若这个坐标系固定在物体上，那么就可以根据上述规则，实现物体的转动、平移。这也是机械臂运动的原理。

愈之~

关注

10
点赞
踩
14

收藏

觉得还不错? 一键收藏
0
评论
第一章机械臂基础-1.1 位姿描述与坐标变换

空间中的一个物体，或者一个点，固定好坐标系之后，就有一个位置坐标，可以用3x1的位置矢量来描述，当然也可以建立多个坐标系，那么对于一个点来说，在不同的坐标系下就有不同的位置坐标，因此需要注明此点在哪个坐标系下的位置坐标，例如，在坐标系。上面的方程公式中，分别阐述了位置和姿态的表示方法，那么一个完成的描述需要将位置与姿态整合，形成新的位姿矩阵，姿态为3x3的单位矩阵，而在机器人中，经常加上一个位置的列矢量，形成新的位姿矩阵，例如在图1.1.2中，将。将（1-1-21）带入（1-1-22）中得到。
复制链接

扫一扫