题目:二次规划基础:二次型、正定矩阵、海塞矩阵
学习二次规划时,需要知道一些基础知识方能看懂,二次型、正定矩阵和半正定矩阵是绕不开的概念,海塞矩阵也是经常要用的名词,所以本篇首先学习一下这三个概念。
1、二次型(文献【1】第127-128页)
主对角线上的元素分别为x2,y2,z2的系数(分别为1,0,3),第1行第2列和第2行第1列两个元素相等,均为xy系数的一半(=-2),第1行第3列和第3行第1列两元素相等,均为xz系数的一半(=0),第2行第3列和第3行第2列两元素相等,均为yz系数的一半(=1/2)。
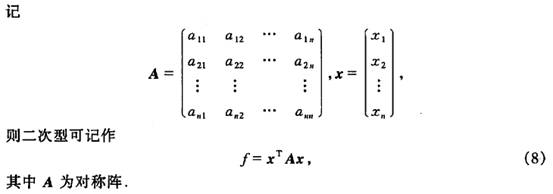
2、正定矩阵(Positive Definite Matrix)(文献【1】第133页)

正定矩阵一定是非奇异的,如何判断对称阵是正定的呢?
如果将正定矩阵的条件xTAx > 0弱化为xTAx≥ 0,则称对称阵A是半定正的。
3、海塞矩阵(HesseMatrix)(文献【2】)
Hesse矩阵最早于19世纪由德国数学家LudwigOtto Hesse提出,并以其名字命名。Hesse矩阵常用于牛顿法解决优化问题。
Hesse矩阵的定义如下:

如果函数f是连续的,则它的Hesse矩阵一定是对称阵:
得到函数f的Hesse矩阵有什么用呢?Hesse可以用于多元函数极值的判定。
下面给两个求Hesse矩阵的例子(文献【3】):
第一个例子:
第二个例子:
参考文献:
【1】同济大学数学系 编. 工程数学线性代数[M]. 5版.高等教育出版社,2007.
【2】Cqbmax. 黑塞矩阵,百度百科,2015-12-18.
【3】春天的下一季. 方向导数与梯度黑塞矩阵与泰勒公式,百度文库,2015-03-24.










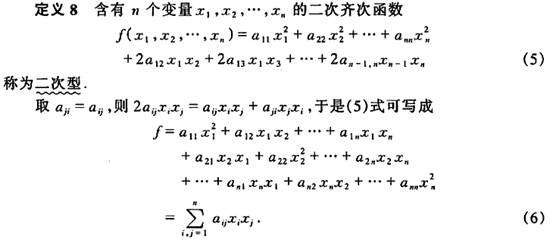
























 1447
1447

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








