六轴机器人轨迹规划之五次多项式插值

最新推荐文章于 2024-09-23 10:02:47 发布

JojenZz

最新推荐文章于 2024-09-23 10:02:47 发布

阅读量3.6w

点赞数 59

分类专栏： Robotics 文章标签：六轴机器人轨迹规划五次多项式插值

本文链接：https://blog.csdn.net/jldemanman/article/details/79303021

版权

Robotics 专栏收录该内容

10 篇文章 168 订阅

订阅专栏

1.轨迹规划的定义
轨迹规划(trajectory planning)是运动规划(motion planning)研究的主要内容。运动规划指的是运动插补，在起始点和终止点之间插入中间点序列，实现沿着轨迹的平稳运动。运动控制包含路径规划(path planning)和轨迹规划，路径规划是规划位置，在起终点之间经过的路径点，轨迹规划是规划时间，将路径点与时间相对应。
对于我们的六轴机器人而言轨迹规划可以分为：关节空间轨迹规划和笛卡尔空间轨迹规划。关节空间轨迹规划是把机器人的关节变量变换成跟时间的函数，然后对角速度和角加速度进行约束。笛卡尔空间轨迹规划是把机器人末端在笛卡尔空间的位移、速度和加速度变换成跟时间的函数关系。
五次多项式插值能够解决三次多项式插值的角速度变化不平滑且加速度存在跳变的情况。
2.数学基础
五次多项式插值，角位移、角速度和角加速度的函数表达式为：

⎧ ⎩ ⎨ ⎪ ⎪ ⎪ ⎪ θ (t) = a 0 + a 1 t + a 2 t 2 + a 3 t 3 + a 4 t 4 + a 5 t 5 θ ˙ (t) = a 1 + 2 a 2 t + 3 a 3 t 2 + 4 a 4 t 3 + 5 a 5 t 4 θ ¨ (t) = 2 a 2 + 6 a 3 t + 12 a 4 t 2 + 20 a 5 t 3

$\begin{eqnarray*} \left\{ \begin{array}{l} \theta(t)=a_0+a_1t+a_2t^2+a_3t^3+a_4t^4+a_5t^5\\ \dot{\theta}(t)=a_1+2a_2t+3a_3t^2+4a_4t^3+5a_5t^4\\ \ddot{\theta}(t)=2a_2+6a_3t+12a_4t^2+20a_5t^3 \end{array}\right. \end{eqnarray*}$
约束条件如下，相对三次多项式插值，增加了对起止点角速度的约束（为简便计算设

t0 t 0 $t_0$ 为0）

⎧ ⎩ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ θ (t 0) = θ 0 = a 0 θ (t f) = θ f = a 0 + a 1 t f + a 2 t 2 f + a 3 t 3 f + a 4 t 4 f + a 5 t 5 f θ ˙ (t 0) = θ ˙ 0 = a 1 θ ˙ (t f) = θ ˙ f = a 1 + 2 a 2 t f + 3 a 3 t 2 f + 4 a 4 t 3 f + 5 a 5 t 4 f θ ¨ (t 0) = θ ¨ 0 = 2 a 2 θ ¨ (t f) = θ ¨ f = 2 a 2 + 6 a 3 t f + 12 a 4 t 2 f + 20 a 5 t 3 f

$\begin{eqnarray*} \left\{ \begin{array}{l} \theta(t_0)=\theta_0=a_0\\ \theta(t_f)=\theta_f=a_0+a_1t_f+a_2t_f^2+a_3t_f^3+a_4t_f^4+a_5t_f^5\\ \dot{\theta}(t_0)=\dot{\theta}_0=a_1\\ \dot{\theta}(t_f)=\dot{\theta}_f=a_1+2a_2t_f+3a_3t_f^2+4a_4t_f^3+5a_5t_f^4\\ \ddot{\theta}(t_0)=\ddot{\theta}_0=2a_2\\ \ddot{\theta}(t_f)=\ddot{\theta}_f=2a_2+6a_3t_f+12a_4t_f^2+20a_5t_f^3 \end{array}\right. \end{eqnarray*}$
求解得

⎧ ⎩ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ a 0 = θ 0 a 1 = θ ˙ 0 a 2 = θ ¨ 0 2 a 3 = 20 θ f - 20 θ 0 - ( 8 θ ˙ f + 12 θ ˙ 0 ) t f - ( 3 θ ¨ 0 - θ ¨ f ) t 2 f 2 t 3 f a 4 = 30 θ 0 - 30 θ f + ( 14 θ ˙ f + 16 θ ˙ 0 ) t f + ( 3 θ ¨ 0 - 2 θ ¨ f ) t 2 f 2 t 4 f a 5 = 12 θ f - 12 θ 0 - ( 6 θ ˙ f + 6 θ ˙ 0 ) t f - ( θ ¨ 0 - θ ¨ f ) t 2 f 2 t 5 f

$\begin{eqnarray*} \left\{ \begin{array}{l} a_0=\theta_0\\ a_1=\dot{\theta}_0\\ a_2=\frac{\ddot{\theta}_0}{2}\\ a_3=\frac{20\theta_f-20\theta_0-(8\dot\theta_f+12\dot\theta_0)t_f-(3\ddot\theta_0-\ddot\theta_f)t_f^2}{2t_f^3}\\ a_4=\frac{30\theta_0-30\theta_f+(14\dot\theta_f+16\dot\theta_0)t_f+(3\ddot\theta_0-2\ddot\theta_f)t_f^2}{2t_f^4}\\ a_5=\frac{12\theta_f-12\theta_0-(6\dot\theta_f+6\dot\theta_0)t_f-(\ddot\theta_0-\ddot\theta_f)t_f^2}{2t_f^5}\\ \end{array}\right. \end{eqnarray*}$
3.matlab代码实现

序号	位移	速度	加速度	时间
1	0	0	0	0
2	50	10	20	3
3	150	20	30	6
4	100	-15	-20	12
5	0	0	0	14

clear;
clc;
q_array=[0,50,150,100,40];%指定起止位置
t_array=[0,3,6,12,14];%指定起止时间
v_array=[0,10,20,-15,0];%指定起止速度
a_array=[0,20,30,-20,0];%指定起止加速度
t=[t_array(1)];q=[q_array(1)];v=[v_array(1)];a=[a_array(1)];%初始状态
for i=1:1:length(q_array)-1;%每一段规划的时间
     T=t_array(i+1)-t_array(i)
     a0=q_array(i);
     a1=v_array(i);
     a2=a_array(i)/2;
     a3=(20*q_array(i+1)-20*q_array(i)-(8*v_array(i+1)+12*v_array(i))*T-(3*a_array(i)-a_array(i+1))*T^2)/(2*T^3);
     a4=(30*q_array(i)-30*q_array(i+1)+(14*v_array(i+1)+16*v_array(i))*T+(3*a_array(i)-2*a_array(i+1))*T^2)/(2*T^4);
     a5=(12*q_array(i+1)-12*q_array(i)-(6*v_array(i+1)+6*v_array(i))*T-(a_array(i)-a_array(i+1))*T^2)/(2*T^5);%计算五次多项式系数 
     ti=t_array(i):0.001:t_array(i+1);
     qi=a0+a1*(ti-t_array(i))+a2*(ti-t_array(i)).^2+a3*(ti-t_array(i)).^3+a4*(ti-t_array(i)).^4+a5*(ti-t_array(i)).^5;
     vi=a1+2*a2*(ti-t_array(i))+3*a3*(ti-t_array(i)).^2+4*a4*(ti-t_array(i)).^3+5*a5*(ti-t_array(i)).^4;
     ai=2*a2+6*a3*(ti-t_array(i))+12*a4*(ti-t_array(i)).^2+20*a5*(ti-t_array(i)).^3;
     t=[t,ti(2:end)];q=[q,qi(2:end)];v=[v,vi(2:end)];a=[a,ai(2:end)];
end
subplot(3,1,1),plot(t,q,'r'),xlabel('t'),ylabel('position');hold on;plot(t_array,q_array,'o','color','g'),grid on;
subplot(3,1,2),plot(t,v,'b'),xlabel('t'),ylabel('velocity');hold on;plot(t_array,v_array,'*','color','y'),grid on;
subplot(3,1,3),plot(t,a,'g'),xlabel('t'),ylabel('accelerate');hold on;plot(t_array,a_array,'^','color','r'),grid on;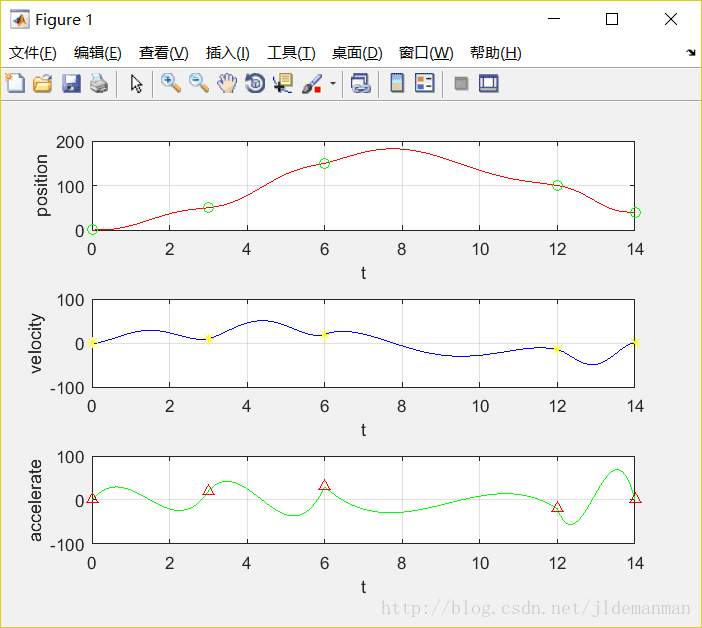

这里写图片描述
PS:相对于三次多项式插值，加速度也是平滑的曲线，并没有出现跳变的情况。然而在机器人系统中，单纯的多项式规划有一个非常严重的问题：没有匀速段，无法根据期望速度提供匀速控制，而在大部分机器人应用中，对加工的速度控制都是有要求的。另一个问题就是，次数越高的多项式，加速过程越慢，整个运动过程中的平均速度越小，影响效率。下次将会为大家介绍能约束速度的三段s曲线加减速直线插值方式。