四元数和旋转(Quaternions and rotations)

文章翻译自Quaternion and rotations，作者Yan-Bin Jia
译者刚入门，水平有限，仅供参考

1. Introduction

2. Quaternion Algebra

本节是四元数的基本性质，可以参考这个链接中的内容，讲的非常详细：https://www.qiujiawei.com/understanding-quaternions/

四元数集，再加上定义在其上的加法和乘法，共同形成了一个不可交换环（non-commutative ring）(这一部分并不需要特别的理解）。
$R^3$空间中的标准正交基为：

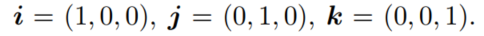
四元数q，被定义成如下形式，由一个数$q_0$和一个向量$\mathbf{q}$，组成：

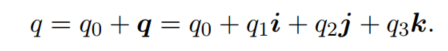
2.1 加法和乘法

加法是逐项进行的，考虑有四元数p：

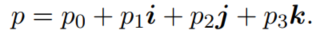
与上文四元数q相加，得到：

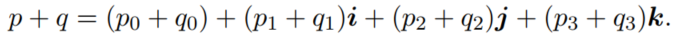
乘法要满足如下的性质：

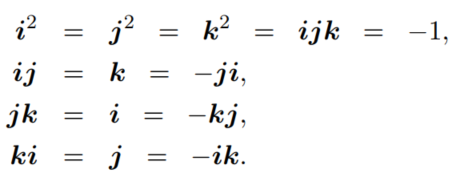
两个四元数相乘可得：

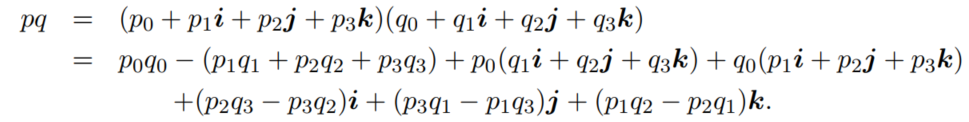
利用向量点乘和向量叉乘的性质，可以化简得：

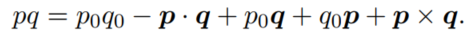
式中：

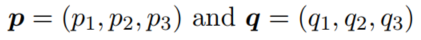
example 1:
假设有如下两个四元数：

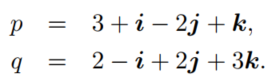
取出向量如下：

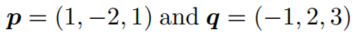
计算向量的点乘和叉乘如下：

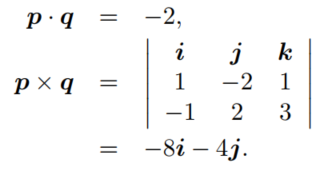
四元数乘积表达如下：

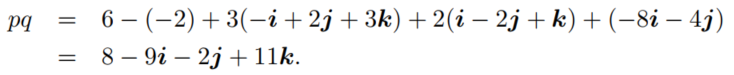
可以看到四元数集对加法和乘法是封闭的

2.2 complex conjugate，Norm and Inverse

假设一个四元数q：

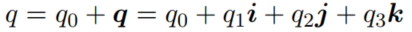
其复共轭为q*：

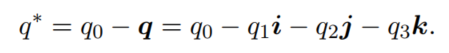
根据上述定义可以得到如下性质：

以及性质：

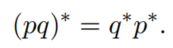
一个四元数的模为：

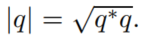
模为1的四元数为单位四元数。模有如下性质：

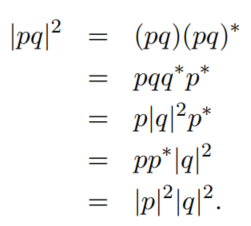
四元数的逆为：

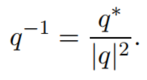
求逆过程证明：

3. Quaternion Rotation Operator

首先定义一个vector，$\mathbf{v}\in R^3$，为实部是0的纯四元数。
紧接着定义一个单位四元数：

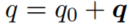
满足：

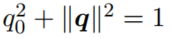
则一定有：

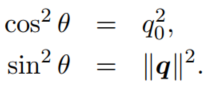
定义单位向量：

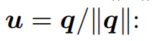
则有：

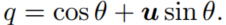
定义一个对于空间向量v的操作：

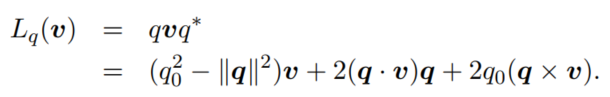
注意这里的证明，要用到如下性质：

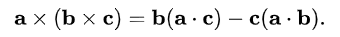
证明：

$$\begin{array}{rl}{L}_q(v\text{v}v)& =qv\text{v}v{q}^{\ast }\\ & =(q_0+q\text{q}q)v\text{v}v(q_0-q\text{q}q)\\ & =(q_{0}v\text{v}v+qv\text{qv}qv)(q_0-q\text{q}q)\\ & =q_0^{2}v\text{v}v+q_{0}qv\text{qv}qv-q_{0}vq\text{vq}vq-qvq\text{qvq}qvq\\ & =q_0^{2}v\text{v}v+q_0(-q\cdot v\text{q⋅v}q\cdot v+q\times v\text{q×v}q\times v)-q_0(-v\cdot q\text{v⋅q}v\cdot q+v\times q\text{v×q}v\times q)-qvq\text{qvq}qvq\\ & =q_0^{2}v\text{v}v+2q_0(q\times v\text{q×v}q\times v)-(-q\cdot v\text{q⋅v}q\cdot v+q\times v\text{q×v}q\times v)q\text{q}q\\ & =q_0^{2}v\text{v}v+2q_0(q\times v\text{q×v}q\times v)-(-q\times v\cdot q\text{q×v⋅q}q\times v\cdot q-(q\cdot v\text{q⋅v}q\cdot v)q\text{q}q+q\times v\times q\text{q×v×q}q\times v\times q)\\ & =q_0^{2}v\text{v}v+2q_0(q\times v\text{q×v}q\times v)+0+(q\cdot v\text{q⋅v}q\cdot v)q\text{q}q+q\text{q}q(q\cdot v\text{q⋅v}q\cdot v)-v\text{v}v(||q\text{q}q|{|}^2)\\ & =(q_0^2-||q\text{q}q|{|}^2)v\text{v}v+2(q\cdot v\text{q⋅v}q\cdot v)q\text{q}q+2q_0(q\times v\text{q×v}q\times v)\end{array}$$

旋转变换不会改变向量v的长度：

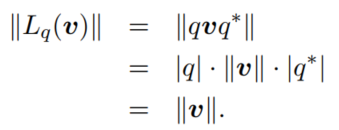
对于沿着旋转轴的向量v进行旋转不会改变方向：

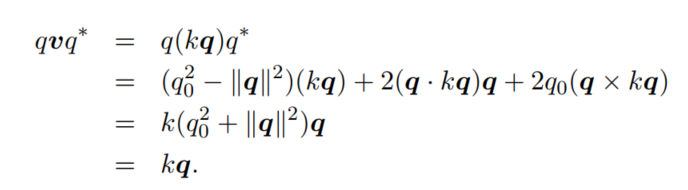
旋转变换是个线性变换：

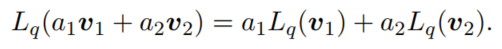
3.1 定理1

对于任意的单位四元数：

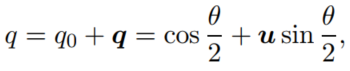
对于任意向量$v\in R^3$进行旋转变换：

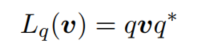
相当于将向量v，绕u轴，旋转$\theta$角度。
证明：TBDD

3.2 定理2

和上面定理1相反，对于任何一个单位四元数：

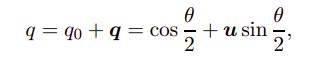
如下操作，是将向量v绕u轴旋转$-\theta$角度：

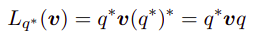
4. Quaternion operator sequence

四元数的序列化操作，也就是先绕一个轴旋转一定角度，再绕另一个轴旋转一定角度。

5. 应用

5.1 3D shape registration

已知一堆点$(p_0,p_1,...,p_n\text{p0,p1,...,pn}{p}_0,p_1,...,p_n)$，另一堆点$(q_0,q_1,...,q_n\text{q0,q1,...,qn}{q}_0,q_1,...,q_n)$，这里应该是知道了对应关系了，求一个变换Ｒ和ｂ满足：

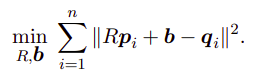
如下图所示：

首先计算点云的重心：

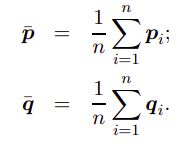
将重心归零：

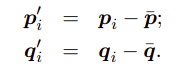
显然有：

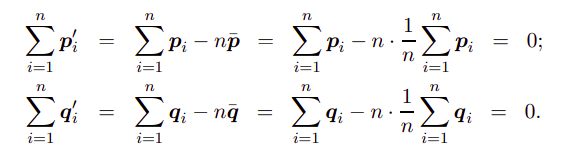
将目标函数重新表达：

上面将Ｒ和ｂ进行了分离，可以分开求解，可见：

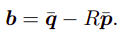
求Ｒ：

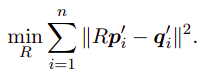
上目标函数重写：

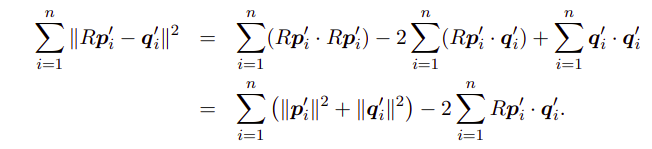
上式可见，第一项与Ｒ无关，只考虑第二项：

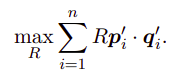
用四元数表示：

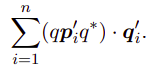
应用四元数求积过程：

将点表达成矩阵形式：

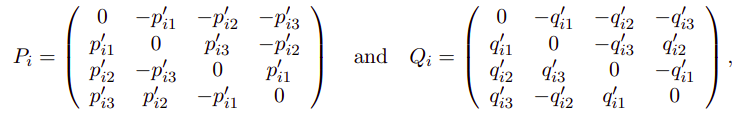
进行改写：


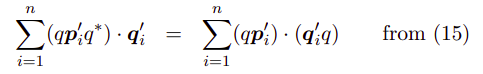
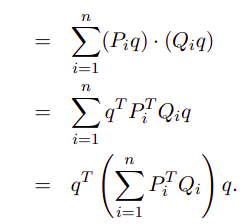
中间部分的矩阵Ｍ是对称的：

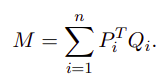
利用特征值特征向量的关系，这里和之前一片文章推倒特征值特征向量及ＳＶＤ的过程基本一致：